最近公共祖先(LCA)
最近公共祖先就是求一颗有根树上,点对$(u,v)$的最近的公共祖先结点。例如如下的一个图中,
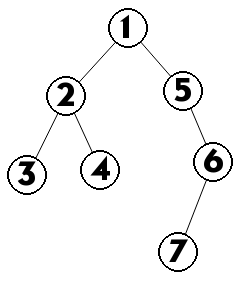
$lca(3,7)=1$,$lca(3,4)=2$。
求任意两点的$LCA$,有离线和在线之分,总共主要有$4$种算法。
离线
这里指已知查询,且无先后顺序影响。
1、Tarjan
首先读入所有的询问对,然后只需一遍$\text{dfs}$即可。
$\text{dfs}$时,首先向下访问子结点,然后并查集中将子结点并入该节点。
当询问对中有一个结点已经访问,又因为是$\text{dfs}$,所以可以得到那个结点的已标记的最上面的祖先结点就是$\text{LCA}$。
不够直观?想象一棵树,该算法就像是从任意一个叶节点开始注水,注到有分叉的时候,水会流向兄弟结点的最底下,继续向上。当查询对的两个点都被水淹没时,最高的水平面中就有其$\text{LCA}$。

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define re register 6 #define rep(i, a, b) for (re int i = a; i <= b; ++i) 7 #define repd(i, a, b) for (re int i = a; i >= b; --i) 8 #define For(i, a, b, s) for (re int i = a; i <= b; s) 9 #define maxx(a, b) a = max(a, b) 10 #define minn(a, b) a = min(a, b) 11 #define LL long long 12 #define INF (1 << 30) 13 14 inline int read() { 15 int w = 0, f = 1; char c = getchar(); 16 while (!isdigit(c)) f = c == '-' ? -1 : f, c = getchar(); 17 while (isdigit(c)) w = (w << 3) + (w << 1) + (c ^ '0'), c = getchar(); 18 return w * f; 19 } 20 21 const int maxn = 5e5 + 5; 22 23 struct Edge { 24 int u, v, pre; 25 } e[maxn << 1]; 26 int ec, G[maxn]; 27 void init() { ec = 0; memset(G, -1, sizeof(G)); } 28 void add(int u, int v) { e[ec++] = (Edge){u, v, G[u]}; G[u] = ec-1; } 29 #define iter(i, u) for (register int i = G[u]; i != -1; i = e[i].pre) 30 31 struct Ques { 32 int v, id, pre; 33 } q[maxn << 1]; 34 int qc, qG[maxn]; 35 void qinit() { qc = 0; memset(qG, -1, sizeof(qG)); } 36 void qadd(int u, int v, int id) { q[qc++] = (Ques){v, id, qG[u]}; qG[u] = qc-1; } 37 #define qiter(i, u) for (register int i = qG[u]; i != -1; i = q[i].pre) 38 int ans[maxn]; 39 // 冰茶姬qwq 40 int fa[maxn]; 41 int fset(int x) { return fa[x] == x ? x : fa[x] = fset(fa[x]); } 42 43 int vis[maxn]; 44 void dfs(int u) { 45 vis[u] = 1; 46 iter(i, u) //遍历所有子结点 47 if (!vis[e[i].v]) { 48 dfs(e[i].v); 49 fa[e[i].v] = u; // 每访问完一棵子树,并入到父亲节点上。 50 } 51 qiter(i, u) // 所有有关于u的询问 52 if (vis[q[i].v]) 53 ans[q[i].id] = fset(q[i].v); 54 } 55 56 int n, m, s; 57 58 int main() { 59 init(); qinit(); 60 n = read(), m = read(), s = read(); 61 rep(i, 1, n-1) { 62 int u = read(), v = read(); 63 add(u, v), add(v, u); 64 } 65 rep(i, 1, m) { 66 int u = read(), v = read(); 67 qadd(u, v, i), qadd(v, u, i); 68 } 69 rep(i, 1, n) fa[i] = i; 70 dfs(s); 71 rep(i, 1, m) printf("%d\n", ans[i]); 72 return 0; 73 }
在线
这里指未知查询,或有先后顺序。
1、倍增
预处理出每一个结点的$2^i,i\text{为非负整数}$的祖先结点和结点深度,然后对于每一组查询$(u,v)$,可以确定$dep[lca(u,v)] \leq min(dep[u], dep[v])$,所以先将深度较大的点跳到与另一个点深度相同的位置,然后判断$u,v$的$2^i$级祖先结点是否相同,如果相同,则说明$LCA$在祖先结点下面的结点里,否则往上跳,最后要么$u=v$,要么正好在$LCA$的孩子结点上。
复杂度:预处理$O(nlogn)$,询问$O(logn)$。
事实上随机情况下,预处理单点和询问复杂度达不到$O(logn)$,而取决于树的深度。最坏情况下树是条链,$log\text{dep}=logn$。
具体详见代码。

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define re register 6 #define rep(i, a, b) for (re int i = a; i <= b; ++i) 7 #define repd(i, a, b) for (re int i = a; i >= b; --i) 8 #define For(i, a, b, s) for (re int i = a; i <= b; s) 9 #define maxx(a, b) a = max(a, b) 10 #define minn(a, b) a = min(a, b) 11 #define LL long long 12 #define INF (1 << 30) 13 14 inline int read() { 15 int w = 0, f = 1; char c = getchar(); 16 while (!isdigit(c)) f = c == '-' ? -1 : f, c = getchar(); 17 while (isdigit(c)) w = (w << 3) + (w << 1) + (c ^ '0'), c = getchar(); 18 return w * f; 19 } 20 21 const int maxn = 5e5 + 5; 22 23 struct Edge { 24 int u, v, pre; 25 } e[maxn << 1]; 26 int G[maxn], ec; 27 void init() { ec = 0; memset(G, -1, sizeof(G)); } 28 void add(int u, int v) { e[ec++] = (Edge){u, v, G[u]}; G[u] = ec-1; } 29 #define iter(i, u) for (register int i = G[u]; i != -1; i = e[i].pre) 30 31 int par[maxn][20], dep[maxn]; 32 int n, m, s; 33 34 void get_fa(int u, int fa) { 35 par[u][0] = fa; dep[u] = dep[fa]+1; 36 rep(i, 1, log2(dep[u])) par[u][i] = par[par[u][i-1]][i-1]; //预处理2^i的祖先结点 37 iter(i, u) 38 if (e[i].v != fa) 39 get_fa(e[i].v, u); 40 } 41 42 #define swap(x, y) x ^= y ^= x ^= y 43 44 int query_lca(int u, int v) { 45 if (dep[u] < dep[v]) swap(u, v); 46 for (register int i = dep[u]-dep[v], j = 0; i; i >>= 1, j++) 47 if (i & 1) u = par[u][j]; //这里运用二进制的技巧倍增跳到同层 48 repd(i, log2(dep[u]), 0) 49 if (par[u][i] != par[v][i]) u = par[u][i], v = par[v][i]; //同层后倍增向上跳 50 return u == v ? u : par[u][0]; 51 } 52 53 int u, v; 54 55 int main() { 56 n = read(), m = read(), s = read(); 57 init(); 58 rep(i, 1, n-1) { 59 u = read(), v = read(); 60 add(u, v), add(v, u); 61 } 62 get_fa(s, s); // 调用时两个参数必须相等,为根结点^_^ 63 rep(i, 1, m) { 64 u = read(), v = read(); 65 printf("%d\n", query_lca(u, v)); 66 } 67 return 0; 68 }
2、欧拉序列+RMQ
首先求出这棵树的欧拉序列;
什么是欧拉序列?就是对有根树进行$\text{DFS}$时,第一次到达结点$u$时记录,访问完每一个子结点后记录$u$,最后得到的序列。
例如上面的树的欧拉序列为$\{1,2,3,2,4,2,1,5,6,7,6,5,1\}$。欧拉序列的长度为$O(n)$,准确来说是$2*n-1$。
然后记录下第一次访问结点$u$时在欧拉序中记录的位置。也就是欧拉序列中$u$第一次出现的位置。
在记录欧拉序列时顺便求下结点深度。
然后可以发现$lca(u,v)=RMQ(pos[u],pos[v]),pos[u]<pos[v]$,其中$\text{RMQ}$的返回值应为结点编号。
这个的优势在于可以$O(1)$查询,但预处理的最坏情况同最优情况一样为$O(nlogn)$。

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define re register 6 #define rep(i, a, b) for (re int i = a; i <= b; ++i) 7 #define repd(i, a, b) for (re int i = a; i >= b; --i) 8 #define For(i, a, b, s) for (re int i = a; i <= b; s) 9 #define maxx(a, b) a = max(a, b) 10 #define minn(a, b) a = min(a, b) 11 #define LL long long 12 #define INF (1 << 30) 13 14 inline int read() { 15 int w = 0, f = 1; char c = getchar(); 16 while (!isdigit(c)) f = c == '-' ? -1 : f, c = getchar(); 17 while (isdigit(c)) w = (w << 3) + (w << 1) + (c ^ '0'), c = getchar(); 18 return w * f; 19 } 20 21 const int maxn = 5e5 + 5; 22 23 struct Edge { 24 int u, v, pre; 25 } e[maxn << 1]; 26 int ec, G[maxn]; 27 void init() { ec = 0; memset(G, -1, sizeof(G)); } 28 void add(int u, int v) { e[ec++] = (Edge){u, v, G[u]}; G[u] = ec-1; } 29 #define iter(i, u) for (register int i = G[u]; i != -1; i = e[i].pre) 30 31 int n, m, s; 32 33 int pos[maxn], tab[maxn][20], L = 0, dep[maxn]; 34 35 void dfs(int u, int fa) { 36 tab[pos[u] = ++L][0] = u; dep[u] = dep[fa] + 1; //记录 37 iter(i, u) 38 if (e[i].v != fa) { 39 dfs(e[i].v, u); 40 tab[++L][0] = u; 41 } 42 } 43 44 void build_st() { //构造Sparse Table 45 rep(i, 1, log2(L)) 46 rep(x, 1, L-(1<<i)+1) 47 tab[x][i] = dep[tab[x][i-1]] < dep[tab[x+(1<<(i-1))][i-1]] ? tab[x][i-1] : tab[x+(1<<(i-1))][i-1]; 48 } 49 50 int query(int x, int y) { // 查询 51 if (x > y) swap(x, y); // 保证x<y 52 int t = log2(y-x); 53 return dep[tab[x][t]] < dep[tab[y-(1<<t)][t]] ? tab[x][t] : tab[y-(1<<t)][t]; 54 } 55 56 int u, v; 57 58 int main() { 59 init(); 60 n = read(), m = read(), s = read(); 61 rep(i, 1, n-1) { 62 u = read(), v = read(); 63 add(u, v); add(v, u); 64 } 65 dfs(s, s); build_st(); 66 rep(i, 1, m) { 67 u = read(), v = read(); 68 printf("%d\n", query(pos[u], pos[v])); 69 } 70 return 0; 71 }
3、树链剖分
不会树剖?去别人那里学习吧(虽然我有一篇博文介绍,但很精简没有时间更新哇qwq)
剖分好路径后根据路径向上走,直到链头相等时,深度小的即为两个的$\text{LCA}$。
预处理为$O(n)$,查询为$O(logn)$。这种方法甚至可以支持树的分裂合并动态修改(好像需要$\text{LCT}$)。
还是看代码理解吧(此处省略1e+9字)

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define re register 6 #define rep(i, a, b) for (re int i = a; i <= b; ++i) 7 #define repd(i, a, b) for (re int i = a; i >= b; --i) 8 #define For(i, a, b, s) for (re int i = a; i <= b; s) 9 #define maxx(a, b) a = max(a, b) 10 #define minn(a, b) a = min(a, b) 11 #define LL long long 12 #define INF (1 << 30) 13 14 inline int read() { 15 int w = 0, f = 1; char c = getchar(); 16 while (!isdigit(c)) f = c == '-' ? -1 : f, c = getchar(); 17 while (isdigit(c)) w = (w << 3) + (w << 1) + (c ^ '0'), c = getchar(); 18 return w * f; 19 } 20 21 const int maxn = 5e5 + 5; 22 23 struct Edge { 24 int u, v, pre; 25 } e[maxn << 1]; 26 int ec, G[maxn]; 27 void init() { ec = 0; memset(G, -1, sizeof(G)); } 28 void add(int u, int v) { e[ec++] = (Edge){u, v, G[u]}; G[u] = ec-1; } 29 #define iter(i, u) for (register int i = G[u]; i != -1; i = e[i].pre) 30 31 int par[maxn], mark[maxn], dep[maxn], link[maxn], topf[maxn], son[maxn], cnt = 0; 32 void dfs1(int u, int fa) { 33 par[u] = fa; dep[u] = dep[fa] + 1; son[link[u] = u] = 1; 34 iter(i, u) 35 if (e[i].v != fa) { 36 dfs1(e[i].v, u); 37 if (son[e[i].v] >= son[link[u]]) link[u] = e[i].v; 38 son[u] += son[e[i].v]; 39 } 40 } 41 void dfs2(int u, int fa, int head) { 42 mark[u] = ++cnt; topf[u] = head; 43 if (link[u] != u) dfs2(link[u], u, head); 44 iter(i, u) 45 if (e[i].v != fa && e[i].v != link[u]) 46 dfs2(e[i].v, u, e[i].v); 47 } 48 #define swap(a, b) a ^= b ^= a ^= b; 49 int query_lca(int u, int v) { 50 while (topf[u] != topf[v]) { 51 if (dep[topf[u]] < dep[topf[v]]) swap(u, v); 52 u = par[topf[u]]; 53 } 54 return dep[u] < dep[v] ? u : v; 55 } 56 57 int n, m, s; 58 int u, v; 59 60 int main() { 61 init(); 62 n = read(), m = read(), s = read(); 63 rep(i, 1, n-1) { 64 u = read(), v = read(); 65 add(u, v); add(v, u); 66 } 67 dfs1(s, s); dfs2(s, s, s); 68 rep(i, 1, m) { 69 u = read(); v = read(); 70 printf("%d\n", query_lca(u, v)); 71 } 72 return 0; 73 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号