[ZJOI2010]排列计数

注意观察题目：$Pi>Pi/2$。

发现特别像什么？

二叉堆！

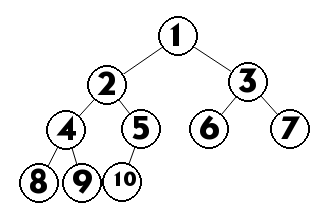
于是就变成了：$n$个堆元素进行排列，满足堆性质的排列对$p$的取模。（堆性质根据题意为大根堆）

设$f_i$为当前堆首为$i$的堆的排列方案数。为满足堆性质$P_i$显然只能取剩下若干数的最大值。

发现$f_i$影响$f_{2i}$和$f_{2i+1}$两个结点。

以$i$为根的堆去掉根节点的结点数为$n-i$个，提前统计出第$i$个结点左子树的大小$size_i$，则右边为$n-i-size_i$个结点。

根据前面，可以得到这样的转移：$f_i=C(n-i,\ size)\times f_{2i}\times f_{2i+1}$。

解释：从剩下的$n-i$个结点中选$size$个结点做其左子树，然后对于每个子树存在$f_{2i}$和$f_{2i+1}$中排列，根据乘法原理即得。

正确性：这些数是一个排列，也就是说任意两个数一定不相等，可以构成一个严格递增的序列。挑出的若干数及挑出若干数后仍能构成严格递增的序列，所以可以化成子问题。

边界：当前根结点为叶节点时，$f_i=1$。

最后答案：$f_1$。

注意：整个$DP$过程是$O(n)$的。但是存在计算组合数，复杂度为$O(n-i)$，$i$为当前根结点。根据递归主定理易知为$O(nlogn)$的复杂度。

存在模数，就要提前处理逆元。对于$p$过小还要用$Lucas$定理，然而数据水而且我不会所以只写了逆元。

#include <bits/stdc++.h>

using namespace std;

#define re register
#define rep(i, a, b) for (re int i = a; i <= b; ++i)
#define repd(i, a, b) for (re int i = a; i >= b; --i)
#define maxx(a, b) a = max(a, b);
#define minn(a, b) a = min(a, b);
#define LL long long
#define inf (1 << 30)

inline int read() {
    int w = 0, f = 1; char c = getchar();
    while (!isdigit(c)) f = c == '-' ? -1 : f, c = getchar();
    while (isdigit(c)) w = (w << 3) + (w << 1) + (c ^ '0'), c = getchar();
    return w * f;
}

const int maxn = 1e6 + 5;

int n, p, f[maxn << 1], g[maxn << 1], inv[maxn];

int C(int n, int m) {
    int res = 1;
    repd(i, n, n-m+1) res = (LL)res * i % p;
    rep(i, 1, m) res = (LL)res * inv[i] % p;
    return res;
}

int dfs(int u) {
    if (u > n) return 0;
    g[u] = dfs(u<<1);
    return g[u] + dfs(u<<1|1) + 1;
}

int dp(int u, int size) {
    if (f[u]) return f[u];
    if (u > n) return f[u] = 1;
    return f[u] = (LL)dp(u<<1, g[u]) * dp(u<<1|1, size-g[u]-1) % p * C(size-1, g[u]) % p;
}

int main() {
    n = read(), p = read();
    inv[1] = 1;
    g[1] = 1;
    rep(i, 2, n) {
        if (i < p)
            inv[i] = (LL)(p-p/i)*inv[p%i] % p;
        else
            inv[i] = inv[i % p];
    }
    dfs(1);
    printf("%d", dp(1, n));
    return 0;
}