[NOIP2013普及组]车站分级

原题传送门

这道题根据题意，能得出该结论：

·一条线路经过的站点，停靠站点等级一定大于未停靠的站点

又因为输入保证所有的车次都满足要求，所以满足偏序集关系。我们可以将站点的大小关系用$DAG$图表示，即将一条线路中停靠站点向未停靠站点连有向边。最后求一遍DAG图中最长链。

问题在于构图的复杂度为$O(n^2m)$，无法接受。

这里采用构建虚点的方式解决构图问题，如下图

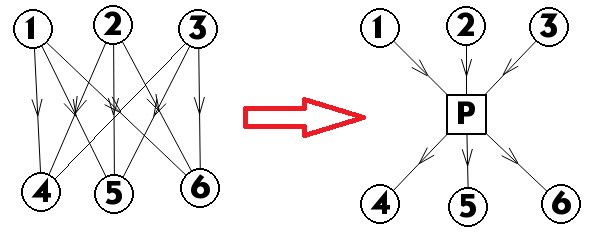
此时复杂度为$O(nm)$。

最后注意最长链包括了虚点，把它去掉即可。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

#define re register
#define rep(i, a, b) for (re int i = a; i <= b; ++i)
#define repd(i, a, b) for (re int i = a; i >= b; --i)
#define maxx(a, b) a = max(a, b);
#define minn(a, b) a = min(a, b);
#define LL long long
#define inf (1 << 30)

inline int read() {
    int w = 0, f = 1; char c = getchar();
    while (!isdigit(c)) f = c == '-' ? -1 : f, c = getchar();
    while (isdigit(c)) w = (w << 3) + (w << 1) + (c ^ '0'), c = getchar();
    return w * f;
}

queue<int> q, q0, empty;

const int maxn = 1e3 + 5;

int a[maxn][maxn], e[maxn << 1][maxn << 1], n, m, r[maxn], d[maxn << 1], ans;

int main() {
    n = read(), m = read();

    rep(i, 1, m) {
        a[i][0] = read();
        memset(r, 0, sizeof(r));
        rep(j, 1, a[i][0]) a[i][j] = read(), r[a[i][j]] = 1;
        rep(j, a[i][1], a[i][a[i][0]]) if (r[j]) e[j][n+i] = 1; else e[n+i][j] = 1;
    }

    rep(i, 1, n+m) {
        rep(j, 1, n+m)
            d[i] += e[j][i] ? 1 : 0;
        if (!d[i]) q.push(i);
    }

    while (!q.empty()) {
        while (!q.empty()) {
            int u = q.front(); q.pop();
            rep(i, 1, n+m) if (e[u][i]) {
                d[i]--;
                if (!d[i]) q0.push(i);
            }
        }
        q = q0; q0 = empty;
        ans++;
    }

    printf("%d", (ans + 1) >> 1);

    return 0;
}