借助Geogebra研究函数图像，并用几何画板交差。

Task 1

1. 用几何画板作出以下函数图象:

\(f_1(x)=\frac{2^x+2^{-x}}{2},\quad f_2(x)=\frac{2^x-2^{-x}}{2},\quad f_3(x)=\log_2(x+\sqrt{x^2-1}),\quad f_4(x)=\log_2(x+\sqrt{x^2+1}).\)

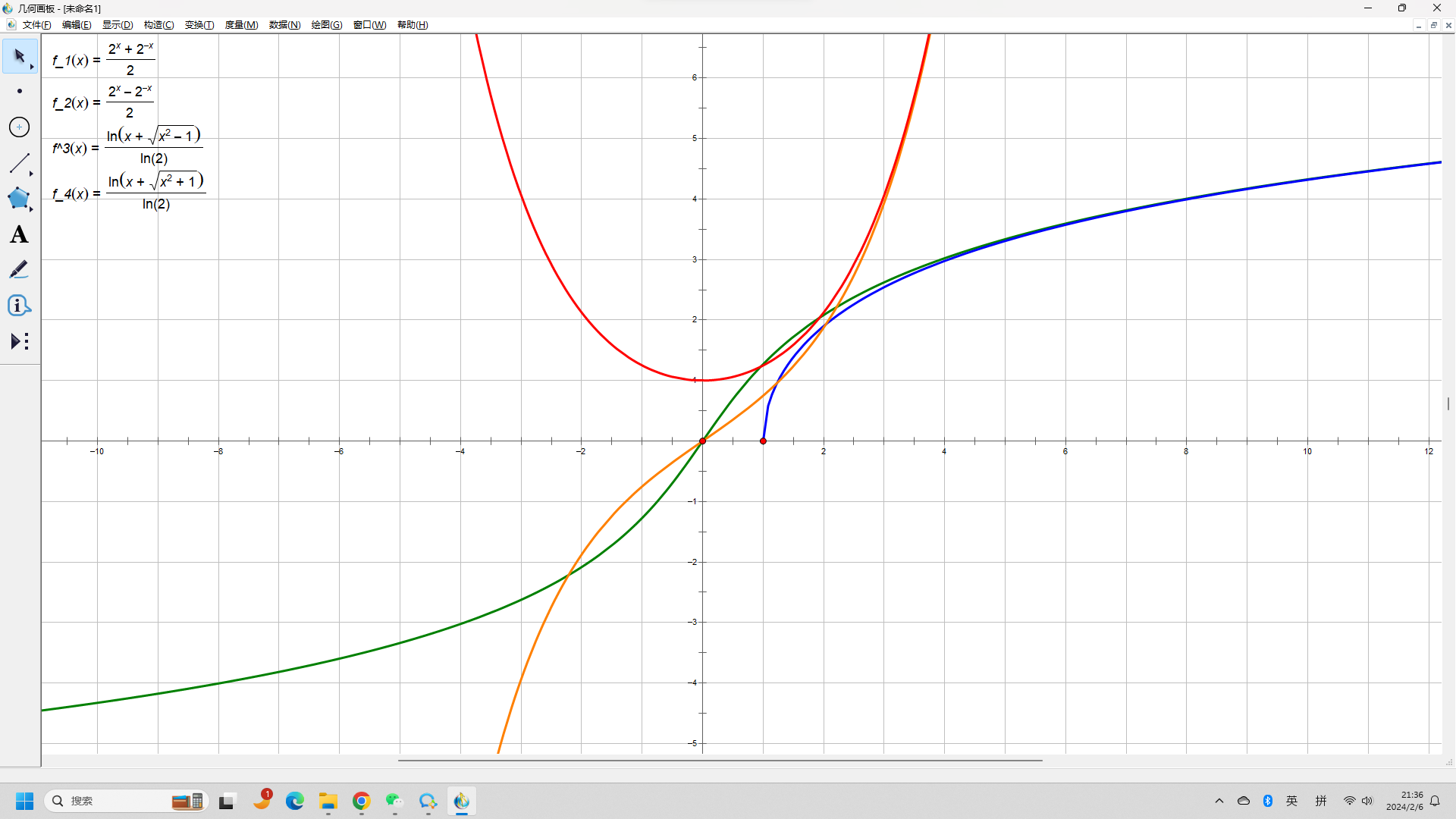
2. 用代数方法解释以上函数图象的定义域、单调性、奇偶性、以及函数图象之间的对称性.

定义域：

\(f_1,\ f_2:\) 显然为 \(\mathbb{R}\)。

\(f_3:\ x+\sqrt{x^2-1}>0 \Rightarrow \begin{cases} -x\geq 0\\ x^2-1>x^2 \end{cases} \text{或} \begin{cases} -x< 0\\ x^2-1\geq 0 \end{cases} \Rightarrow x\geq 1\)

\(f_4:\ x+\sqrt{x^2+1}>0 \Rightarrow \begin{cases} -x\geq 0\\ x^2+1>x^2 \end{cases} \text{或} \begin{cases} -x< 0\\ x^2+1\geq 0 \end{cases} \Rightarrow x\in \mathbb{R}\)

单调性：

\(f_1:\ \because x+\frac{1}{x}\ (x>0)\) 在 \((0,1)\) 上单减，\((1,+\infty)\) 上单增，\(\therefore \frac{2^x+\frac{1}{2^x}}{2}\) 在 \((-\infty,0)\) 上单减，\((0,\infty)\) 上单增。

\(f_2:\ \because x-\frac{1}{x}\ (x>0)\) 在 \(\mathbb{R}\) 上单减，\((1,+\infty)\) 上单增，\(\therefore \frac{2^x-\frac{1}{2^x}}{2}\) 在 \(\mathbb{R}\) 上单减。

\(f_3:\ \because \log_2(x),x,\sqrt{x},x^2-1\) 均单增，\(\therefore f_3\) 单增。

$f_4:\ $与 \(f_3\) 相似。

奇偶性：

\(f_1:\ f_1(-x)=\frac{2^{-x}+2^x}{2}=f_1(x)\)，偶。

\(f_2:\ f_2(-x)=\frac{2^{-x}-2^x}{2}=-f_2(x)\)，奇。

$f_3:\ $由定义域，无奇偶。

\(f_4:\ f_4(x)+f_4(-x)=\log_2((x+\sqrt{x^2+1})(-x+\sqrt{x^2+1})).\) 只需证 \(\log\) 里面的东西 \(=1\)：

\((x+\sqrt{x^2+1})(-x+\sqrt{x^2+1})=-x^2+x\sqrt{x^2+1}-x\sqrt{x^2+1}+x^2+1=1.\)

对称性：

\(f^{-1}_1(x):\ x=\frac{2^y+2^{-y}}{2}\Rightarrow 2^y+2^{-y}=2x.\) 然后就不会解啦

\(f^{-1}_2(x):\ x=\frac{2^y-2^{-y}}{2}\Rightarrow 2^y-2^{-y}=2x.\) 然后也不会解啦

Task 2

1. 用几何画板作出以下函数图象:

\(f_1(x)=\frac{2^x-1}{2^x+1},\quad f_2(x)=\frac{2^x+1}{2^x-1},\quad f_3(x)=\log_2\frac{1+x}{1-x},\quad f_4(x)=\log_2\frac{x+1}{x-1}.\)

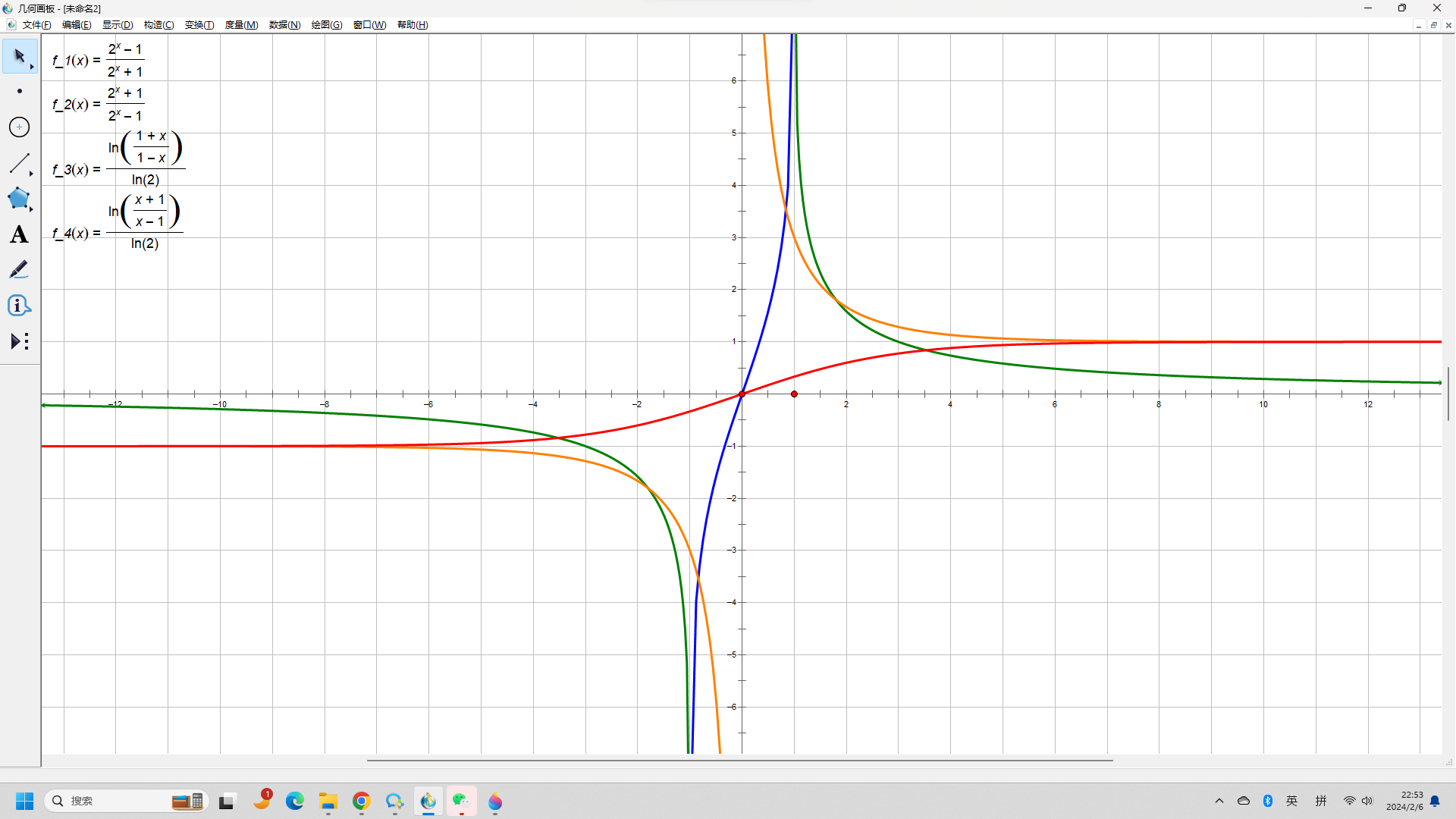
2. 用代数方法解释以上函数图象的定义域、单调性、奇偶性、以及函数图象之间的对称性.

定义域：

\(f_1:\ 2^x+1\neq 0\Rightarrow x\in \mathbb{R}\)。

\(f_2:\ 2^x-1\neq 0\Rightarrow x\in(-\infty,0)\cup(0,+\infty)\)。

\(f_3:\ \frac{1+x}{1-x}>0\Rightarrow(x+1)(x-1)<0\Rightarrow -1<x<1\)。

$f_4:\ $ 同理，\(x\in(-\infty,-1)\cup(1,+\infty)\)。

零点：

\(f_1:\ 2^x-1=0\Rightarrow x=0\)。

\(f_2:\ 2^x+1=0\Rightarrow x\in\emptyset\)。

\(f_3:\ \frac{1+x}{1-x}=1\Rightarrow 1+x=1-x\Rightarrow x=0\)。

\(f_4:\ \frac{x+1}{x-1}=1\Rightarrow x+1=x-1\Rightarrow x\in\emptyset\)。

渐近线：

怎么做？？

单调性：

\(f_1=1-\frac{2}{2^x+1}\)，单增。

\(f_2=1+\frac{2}{2^x-1}\)，在 \((-\infty,0)\)，\((0,\infty)\) 上单减。

\(f_3:\ \because \frac{1+x}{1-x}=-1-\frac{2}{x-1}\) 在 \((-1,1)\) 上单增，\(\therefore f_3\) 单增。

\(f_4:\)