初三奥赛模拟测试3
初三奥赛模拟测试3
T1 网格图

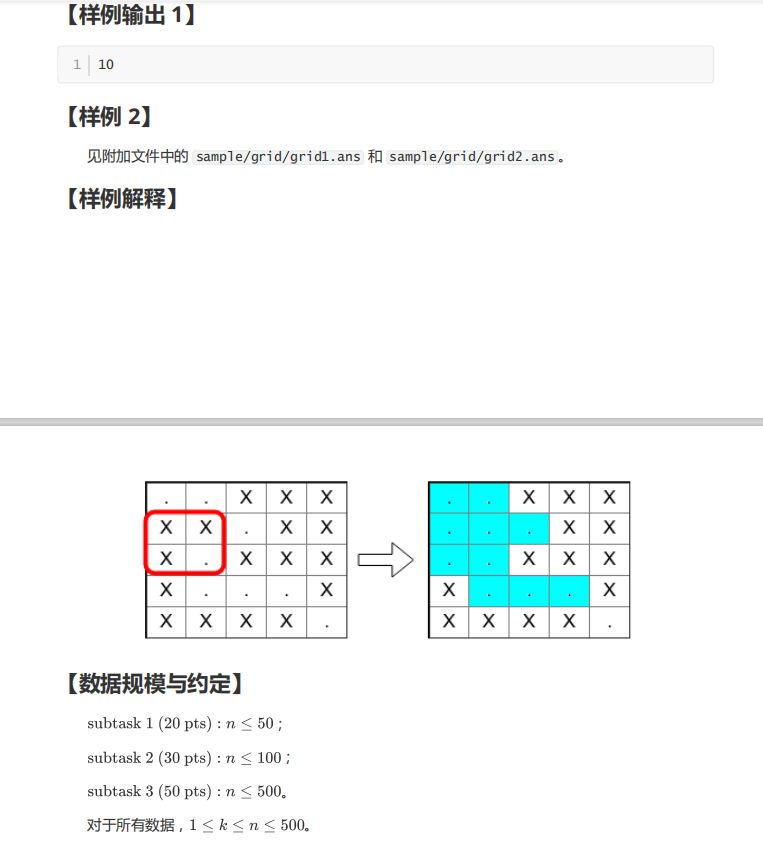
开幕雷击,T1先做2h,糊了个玄学复杂度的做法,会被点叉相交的数据卡,不过数据水,放过去了。
考虑正解,枚举正方形可能出现的情况,对于每个正方形,尝试从上一个正方形转移,经过一些预处理,可以做到 $ O(n) $ 转移。
懒得写正解了,去看其他 HZOIers 的题解吧
T2 序列问题

数据范围
对于 $ 100 % $ 的数据 ,保证 $ n \le 5 \times 10^5 ,1 \le A_i \le 10^9 $
做法
部分分
一眼看去比较像最长上升子序列,但没想到正解,打了一个 $ O(n^2) $ 的暴力DP,设 $ dp[i] $ 为第i的位置的最多匹配数量。
我们发现:如果i可以由j转移过来,一定满足:
- $ i > j $
- $ a_i > a_j $
- $ a_i-i \le a_j-j $
因此得到转移方程
这里我们发现神奇性质,当满足条件2,3时,也一定满足条件1。
正解
一个晚三想到可行做法,我们预处理 $ c_i=a_i-i $
为满足条件2,我们可以按照 $ a_i $ 升序排序,这样保证 $ \forall i>j,a_i \ge a_j $
为满足条件3,按 $ c_i $ 降序排序,依次修改DP值,这样以时间为轴,在这之前的都可以转移。
我们现在需要查询前缀最大值,并支持单点修改,不难想到树状数组,这种做法正确性显然。
Code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int n;
struct node{
int id,val;
}a[N];
struct nod{
int ch,id,be;
}c[N];
int ans,s[N],dp[N],b[N];
bool cmp1(node x,node y){
if(x.val==y.val)return x.id<y.id;
else return x.val<y.val;
}
bool cmp2(nod x,nod y){
if(x.ch==y.ch)return x.id<y.id;
else return x.ch>y.ch;
}
inline int lowbit(int x){
return x&(-x);
}
void change(int x,int y){
while(x<=n){
s[x]=max(s[x],y);
x+=lowbit(x);
}
}
int query(int x){
int ans=0;
while(x>0){
ans=max(ans,s[x]);
x-=lowbit(x);
}
return ans;
}
int main()
{
freopen("sequence.in","r",stdin);
freopen("sequence.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i].val);
a[i].id=i;
}
sort(a+1,a+n+1,cmp1);
for(int i=1;i<=n;i++){
c[i]=nod{a[i].val-a[i].id,i,0};
if(a[i].val==a[i-1].val)b[i]=b[i-1]+1;
}
sort(c+1,c+n+1,cmp2);
for(int i=1;i<=n;i++){
if(c[i].ch>0)continue;
dp[c[i].id]=query(c[i].id-b[c[i].id]-1)+1;
change(c[i].id,dp[c[i].id]);
ans=max(ans,dp[c[i].id]);
}
printf("%d",ans);
}
看了官方题解后觉得自己唐氏了,既然已经预处理 \(c_i\) ,并排序后,这不就是最长上升子序列嘛...
T3 置换
什么是置换?
不会,咕了。
T4 同桌的你

一眼不会,听完局长讲解后大彻大悟。
正解
我们不妨将“被喜欢”的关系作为单向边,进行建树,形成一片森林,我们发现有n个节点,n条边,并不是严格意义上的树。
对于每棵树的节点,入度一定为1,可以证明每棵树上一定有且仅有一个环,对于这个环,如果选择当前边不是最优的,一定是与它相邻的边存在更优答案。
考虑在每个环上找出两个相邻的边,每次将其中一个标记一下,dfs时不再经过这条边,然后就是套路的树形DP,记录路径。
这里有一个小技巧,我们令V为一个大于值域的数,定义一组同桌存在喜欢关系价值是V,在此基础上为异性价值是1。
$ ans1= \left \lfloor \frac{ans}{V} \right \rfloor ,ans2= ans \mod V $
记得写快读,不然可能会T。
关于评测机波动,我的评价是多交几遍,总会A的。
Code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e6+100;
const int V=1e9;
int T,n,a[N],b[N],head[N],cnt,fa[N],broke1,broke2,id[N];
bool vis[N],flag,drop[N];
ll maxn[4][N];
ll dp[2][N][2],ans[N],pre[2][N];
int tot=0;
struct edge{
int from,to,next;
ll val;
}e[N];
stack<int>st;
vector<int>p;
queue<int>q;
int read(){
int w=0;
char c=getchar();
while(c>'9'||c<'0')c=getchar();
while(c>='0'&&c<='9'){
w=w*10+c-'0';
c=getchar();
}
return w;
}
void write(int x){
if(x>=10)write(x/10);
putchar(x%10+'0');
}
inline ll Max(ll x,ll y){
if(x>y)return x;
else return y;
}
void clear(){
cnt=0;tot=0;
memset(maxn,0,sizeof(maxn));
memset(vis,0,sizeof(vis));
memset(drop,0,sizeof(drop));
memset(ans,0,sizeof(ans));
memset(head,0,sizeof(head));
memset(dp,0,sizeof(dp));
memset(pre,0,sizeof(pre));
}
void add(int u,int v,int w){
cnt++;
e[cnt].from=u;
e[cnt].to=v;
e[cnt].next=head[u];
e[cnt].val=w;
head[u]=cnt;
}
void dfs1(int x){
if(flag)return ;
if(vis[x]){
while(!st.empty()&&e[st.top()].from!=x){
if(!broke1)broke1=st.top();
else if(!broke2)broke2=st.top();
st.pop();
}
if(!st.empty()){
if(!broke1)broke1=st.top();
else if(!broke2)broke2=st.top();
st.pop();
}
flag=1;
return ;
}
vis[x]=1;
drop[x]=1;
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
st.push(i);
dfs1(y);
if(!st.empty())
st.pop();
}
vis[x]=0;
}
void bfs(int x,int t){
q.push(x);
p.push_back(x);
vis[x]=1;
while(!q.empty()){
x=q.front();
q.pop();
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(!vis[y]){
vis[y]=1;
p.push_back(y);
q.push(y);
}
}
if(!vis[fa[x]]){
vis[fa[x]]=1;
p.push_back(fa[x]);
q.push(fa[x]);
}
}
while(!p.empty()){
id[p.back()]=t;
p.pop_back();
}
}
void dfs2(int x,int bre,int times){
for(int i=head[x];i;i=e[i].next){
if(i==bre)continue;
int y=e[i].to;
if(!Max(dp[times][y][0],dp[times][y][1]))
dfs2(y,bre,times);
dp[times][x][0]+=Max(dp[times][y][0],dp[times][y][1]);
}
for(int i=head[x];i;i=e[i].next){
if(i==bre)continue;
int y=e[i].to;
if(dp[times][x][0]-Max(dp[times][y][0],dp[times][y][1])+dp[times][y][0]+e[i].val>dp[times][x][1]){
dp[times][x][1]=dp[times][x][0]-Max(dp[times][y][0],dp[times][y][1])+dp[times][y][0]+e[i].val;
pre[times][x]=y;
}
}
}
void dfs3(int x,bool pd,int times){
if(vis[x])return ;
vis[x]=1;
if(pd==1){
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(vis[y])continue;
if(y==pre[times][x]){
write(x);putchar(' ');write(y);puts("");
dfs3(y,0,times);
}
else{
if(dp[times][y][1]>dp[times][y][0]){
dfs3(y,1,times);
}
else{
dfs3(y,0,times);
}
}
}
}
else{
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(vis[y])continue;
if(dp[times][y][0]>dp[times][y][1]){
dfs3(y,0,times);
}
else{
dfs3(y,1,times);
}
}
}
}
int main()
{
freopen("deskmate.in","r",stdin);
freopen("deskmate.out","w",stdout);
T=read();
while(T--){
n=read();
clear();
for(int i=1;i<=n;i++){
a[i]=read();b[i]=read();
b[i]=(b[i]&1);
fa[i]=a[i];
}
for(int i=1;i<=n;i++){
add(a[i],i,V+(b[i]^b[a[i]]));
}
for(int i=1;i<=n;i++){
if(!vis[i]){
bfs(i,++tot);
}
}
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++){
if(!drop[i]){
flag=0;broke1=broke2=0;
while(!st.empty())st.pop();
dfs1(i);
if(!flag)continue;
dfs2(e[broke1].to,broke1,0);
dfs2(e[broke2].to,broke2,1);
}
}
for(int i=1;i<=n;i++){
ans[id[i]]=Max(ans[id[i]],Max(dp[0][i][1],dp[1][i][1]));
if(maxn[0][id[i]]<dp[0][i][1]){
maxn[0][id[i]]=dp[0][i][1];
maxn[2][id[i]]=i;
}
if(maxn[1][id[i]]<dp[1][i][1]){
maxn[1][id[i]]=dp[1][i][1];
maxn[3][id[i]]=i;
}
}
ll sum=0;
for(int i=1;i<=tot;i++){
sum+=ans[i];
}
ll ans1=sum/V,ans2=sum%V;
write(ans1);putchar(' ');write(ans2);puts("");
for(int i=1;i<=tot;i++){
if(maxn[0][i]>maxn[1][i]){
dfs3(maxn[2][i],1,0);
}
else{
dfs3(maxn[3][i],1,1);
}
}
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号