Codeforces 587B Duff in Beach

D. Duff in Beach

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

While Duff was resting in the beach, she accidentally found a strange array b0, b1, ..., bl - 1 consisting of l positive integers. This array was strange because it was extremely long, but there was another (maybe shorter) array, a0, ..., an - 1 that b can be build from a with formula: bi = ai mod n where a mod b denoted the remainder of dividing a by b.

Duff is so curious, she wants to know the number of subsequences of b like bi1, bi2, ..., bix (0 ≤ i1 < i2 < ... < ix < l), such that:

• 1 ≤ x ≤ k
• For each 1 ≤ j ≤ x - 1, 
• For each 1 ≤ j ≤ x - 1, bij ≤ bij + 1. i.e this subsequence is non-decreasing.

Since this number can be very large, she want to know it modulo 109 + 7.

Duff is not a programmer, and Malek is unavailable at the moment. So she asked for your help. Please tell her this number.

Input

The first line of input contains three integers, n, l and k (1 ≤ n, k, n × k ≤ 106 and 1 ≤ l ≤ 1018).

The second line contains n space separated integers, a0, a1, ..., an - 1 (1 ≤ ai ≤ 109 for each 0 ≤ i ≤ n - 1).

Output

Print the answer modulo 1 000 000 007 in one line.

Sample test(s)

input

3 5 3
5 9 1

output

10

input

5 10 3
1 2 3 4 5

output

25

Note

In the first sample case, 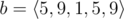. So all such sequences are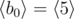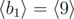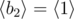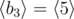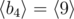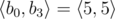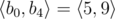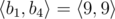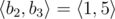: , , , , , , , ,  and .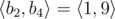

有点类似前几场一个题 一个区间复制好多次求最长不下降序列长度 然而还是没过那个题

这个要求就是必须在连续段里选择

先给a排一下序

所以sum[i][j]表示总长度为i,最后一位是第j个数时的方案

一开始以为

sum[i][j]=sigma[i-1][j]

sigma[i][j]=sigma[i][j-1]+sum[i][j]

其实这样是错误的

因为可能出现重复数字的情况

比如

2 5 3

1 1

sum[1][1]=sum[1][2]=1;

sum[2][1]=2;不是1

所以应该找到数组中小于等于自己的最大的那个pos

=sigma[i-1][pos]就对了

然后分两种情况

如果有不能正好分完的情况

1.需要的组数全在正好分完的组里挑

2.需要的组数中最后一组在不完整的最后那组里选，其他的在完整的组里选

还要注意一点 long long a = 两个int相乘时 需要在第一个int前面先强制转换成long long 再乘

参见代码

#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
const int lim=1e6+10;
long long m,n;
long long l;
int f[lim];
int g[lim];
long long shengxia;
int need[lim];
vector<long long>sum[lim],sigma[lim];
long long duan;

int main()
{
    //freopen("1.in","r",stdin);
    //freopen("1.out","w",stdout);
    cin>>m>>l>>n;
    for(int i=1;i<=m;i++)
    {
        //cin>>f[i];
        scanf("%d",&f[i]);
    }
    shengxia = l%m;
    for(int i=1;i<=shengxia;i++)
        g[i]=f[i];
    sort(f+1,f+m+1);
    sort(g+1,g+shengxia+1);
    for(int i=1;i<=m;i++)
    {
        need[i-1]=upper_bound(f+1,f+m+1,f[i])-f-2;
    }
    long long pre = l/m;
    long long duan=min((long long)n,(long long)pre+(l%m==0?0:1));
    //cout<<duan<<" "<<shengxia<<" "<<pre<<endl;
    for(int i=0;i<duan;i++)
    {
        int len = i+1;
        for(int j=0;j<m;j++)
        {
            if(len==1)
                sum[len].push_back(1);
            else
                sum[len].push_back(sigma[len-1][need[j]]%mod);
//cout<<"sum["<<len<<"]["<<sum[len].size()-1<<"]="<<sum[len][sum[len].size()-1]<<endl;
            if(j==0)
                sigma[len].push_back(sum[len][j]%mod);
            else
                sigma[len].push_back((sigma[len][j-1]+sum[len][j])%mod);

        }
    }
    long long ans=0;

    for(int i=1;i<=duan&&i<=pre;i++)
        for(int j=0;j<m;j++)
        {
//cout<<" A="<<pre-i+1<<" i="<<i<<" num="<<sum[i][j]<<endl;
                int value=f[i];
                ans=((long long)ans+(long long)(((pre-i+1)%mod)*sum[i][j]%mod))%mod;
//cout<<ans<<endl;
        }
    if(shengxia!=0)
    {
        ans=(ans+shengxia)%mod;
//cout<<"ans="<<ans<<endl;
        for(int i=1;i<=duan-1 && i<=pre;i++)
        {
            for(int j=1;j<=shengxia;j++)
            {
                int value=g[j];
                int pos=upper_bound(f+1,f+m+1,value)-f-2;
//cout<<"pos="<<pos<<endl;
//cout<<g[j]<<" "<<f[pos+1]<<endl;
//cout<<"simga["<<i<<"]["<<pos<<"]="<<sigma[i][pos]<<endl;
//cout<<"value="<<value<<" pos="<<pos<<" sigma="<<sigma[i][pos-1]<<endl;
                ans=((long long)ans+(long long)(sigma[i][pos]))%mod;
//cout<<"i="<<i<<" ans="<<ans<<endl;
            }
        }
    }
    cout<<ans%mod<<endl;
}