AC 自动机

前置知识

字符串匹配

初学字符串的时候，我们会遇到这样一个问题，对于一个长度为 \(n\) 的字符串 \(S\)，对于一个长度为 \(m\) 的字符串 \(T\)，求 \(T\) 是不是 \(S\) 的连续子串。

• 初学时，我们可以暴力枚举 \(S\) 数组中所有长度为 \(m\) 的子序列，判断他们与 \(T\) 的关系，时间复杂度 \(O(n\times m)\)。
• 利用 KMP 算法，可以通过与处理 nxt 数组，从而以 \(O(n+m)\) 的时间复杂度解决。

在学习 AC 自动机之前，我们需要首先了解 KMP 算法的实现过程。

trie 树

trie 树，字典树，是一种通过动态开点动态存储和查询字符串的数据结构，trie 的变形（如：01 trie）也是解决按位运算操作问题的主要解决方式。

如果我们将一下单词存入一棵 trie 树，那么会形成下面的结构：
（依次加入：she、he、zc、her、hip、hef、shit、shis）

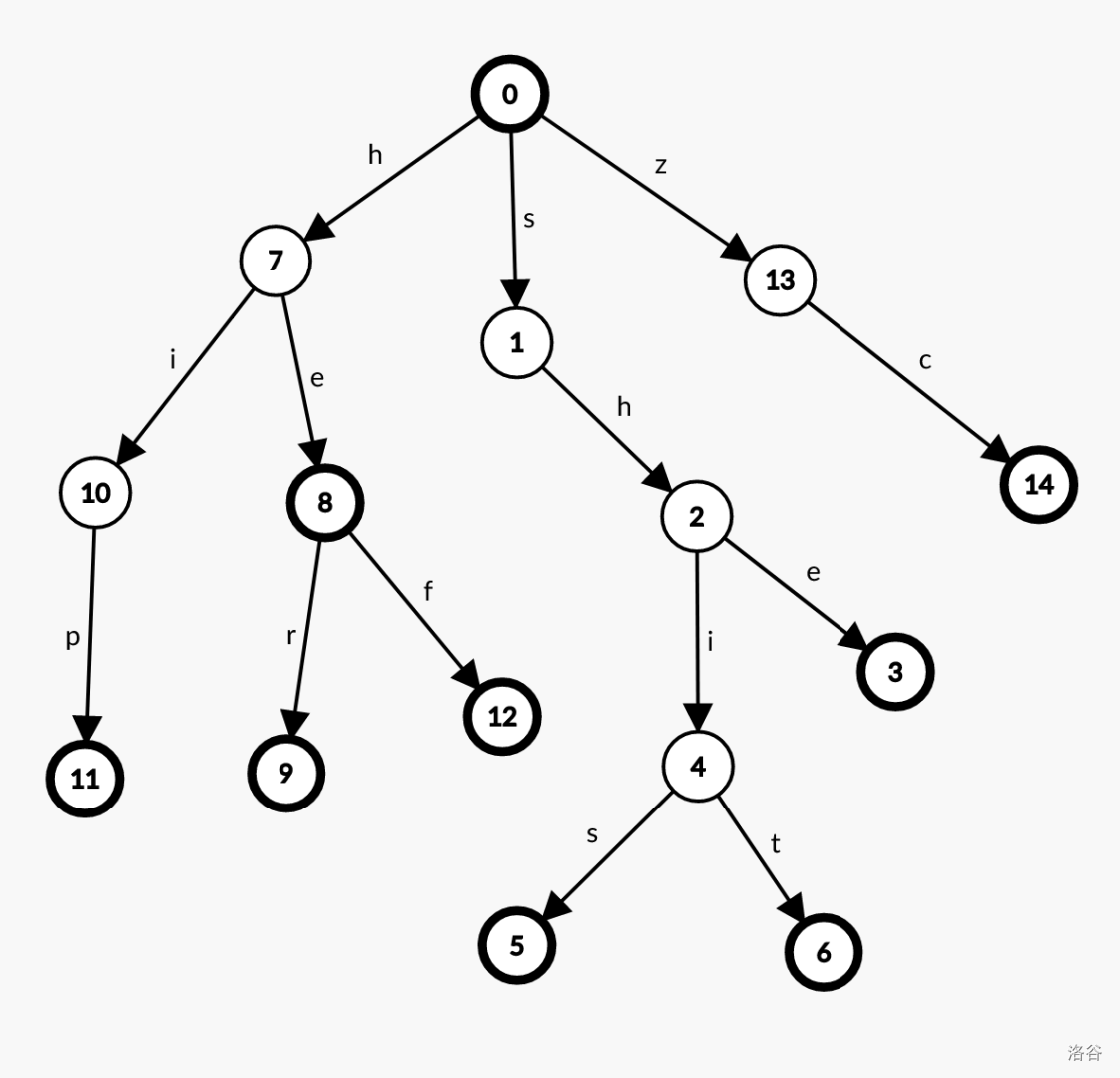
引入问题

考虑这样一种情况，当我们审核一篇文章或者一份代码时，需要判断其中是否含有暴戾语言，对于一片很长的文章，我们有很多的暴戾文字不能出现，如何能够以很快的速度判断呢？

考虑以下做法：

• 对于每一个语言，逐个遍历，使用暴力判断或 KMP 进行求解；

若我们的目标串 \(S\) 的长度为 \(n\leq 10^6\)，模式串一共 \(m\leq 10^6\) 个，且 \(\sum_{i=1}^{m} |T_i|\leq 10^6\)，那么，在极限情况下，KMP 也是不可过的，这样，我们就需要一种新的算法 —— AC 自动机。

AC 自动机，Aho - Corasick automaton，该算法在 \(1975\) 年产生于贝尔实验室，是著名的多模匹配算法。

AC 自动机实质上是 trie 树，KMP 中的 nxt 数组和广度优先搜索的完美结合。

实现

建树

首先，根据所有的模式串，建立一棵包含所有结点的 trie 树。

简述之后，我们可以很容易想到一种朴素做法：

朴素做法：

在先建立了 trie 树之后，我们从 \(i\) 从 \(1\sim |s|\) 进行遍历，对于每一个 \(i\)，从第 \(i\) 个字符开始，往下依次移动，看看往下移动到的结点的有多少个单词包含在其中。

代码大致如下：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+7;
struct node {
	int ch[N][26];
	int ed[N],tot;
	void insert(string s) {
		int cur=0;
		for(int i=0;i<s.size();++i) {
			int c=s[i]-'a';
			if(!ch[cur][c]) ch[cur][c]=++tot;
			cur=ch[cur][c];
		} ed[cur]++;
	} //建立 trie 树
	int query(string s) {
		int res=0;
		for(int i=0;i<s.size();++i) {
        	//对于每一个 i，在 trie 树上匹配
			int cur=0,j=i;
			while(j<s.size()) {
				res+=ed[cur];
				ed[cur]=0;
				if(!ch[cur][s[j]-'a']) break;
				cur=ch[cur][s[j]-'a'],++j;
			}
		} return res;
        //查询操作
	}
} trie;
int main() {
	int n;
	cin>>n;
	while(n--) {
		string s;
		cin>>s;
		trie.insert(s);
	} string t;
	cin>>t;
	cout<<trie.query(t);
	return 0;
}

这个代码在洛谷模板题中可以拿到 \(50\) 分。

建立回跳边

对失配后和链上走到头了之后从头开始匹配的这个操作进行优化，很容易想到 KMP 算法中类似的 \(nxt\) 数组，建立 \(nxt\) 数组的方式简而言之就是：先进行一次 bfs 处理 \(nxt\) 数组，\(nxt[u]\) 的定义为到 \(u\) 节点路径上的单词的最长后缀在什么位置，类似于 KMP，也就是失配后最长能够继续匹配的位置。

也就是说，如果我们的两个串是下述情况：

pos:0123456789
s:  abcdabcdef
t1: abcdabcea
t2:    dabcdef

我们现在有两个模式串 \(t_1\) 和 \(t_2\)，到匹配到标准串 \(s\) 的第 \(7\) 个字符时，可以发现模式串 \(t_1\) 匹配失败了（失配了），那么我们应到跳到模式串 \(t_2\) 的第 \(7\) 个字符继续匹配，也就是说，对于 \(t_1\) 第 \(7\) 个点对应 trie 树中的节点，我们应连一条回跳边到 \(t_2\) 第 \(7\) 个点所对应的 trie 树中的节点。

但是，问题来了，所有的适配情况都一样吗？是不是所有适配情况都是这样呢？

我们来看下面这个例子：

pos:0123456789
s1: abcdabcsed
s2: abcdabcded
t1: abcdabcea
t2:    dabcded
t3:    dabcsed

通过观察，我们可以发现，\(t_1\) 还是到第 \(7\) 个位置开始失配，此时，我们的回跳边应该连到 \(t_2\) 还是 \(t_3\) 呢？如果模式串 \(s\) 是 \(s_1\) 这种情况，那么回跳边应该连到 \(t_3\)，如果模式串为 \(s_2\) 这种情况，回跳边就应该连到 \(t_2\) 了，这让我们进退两难，所以，在处理这种情况是，我们考虑不直接建边，而是对于儿子进行补充，即令 \(t_1\) 第 \(6\) 个点对应 s 的儿子连到 \(t_2\) 第 \(7\) 个点，令 \(t_1\) 第 \(6\) 个点对应 d 的儿子连到 \(t_2\) 第 \(7\) 个点即可，建完后，整个 trie 树如下图（红色的边为回跳边，黑色为转移边）。

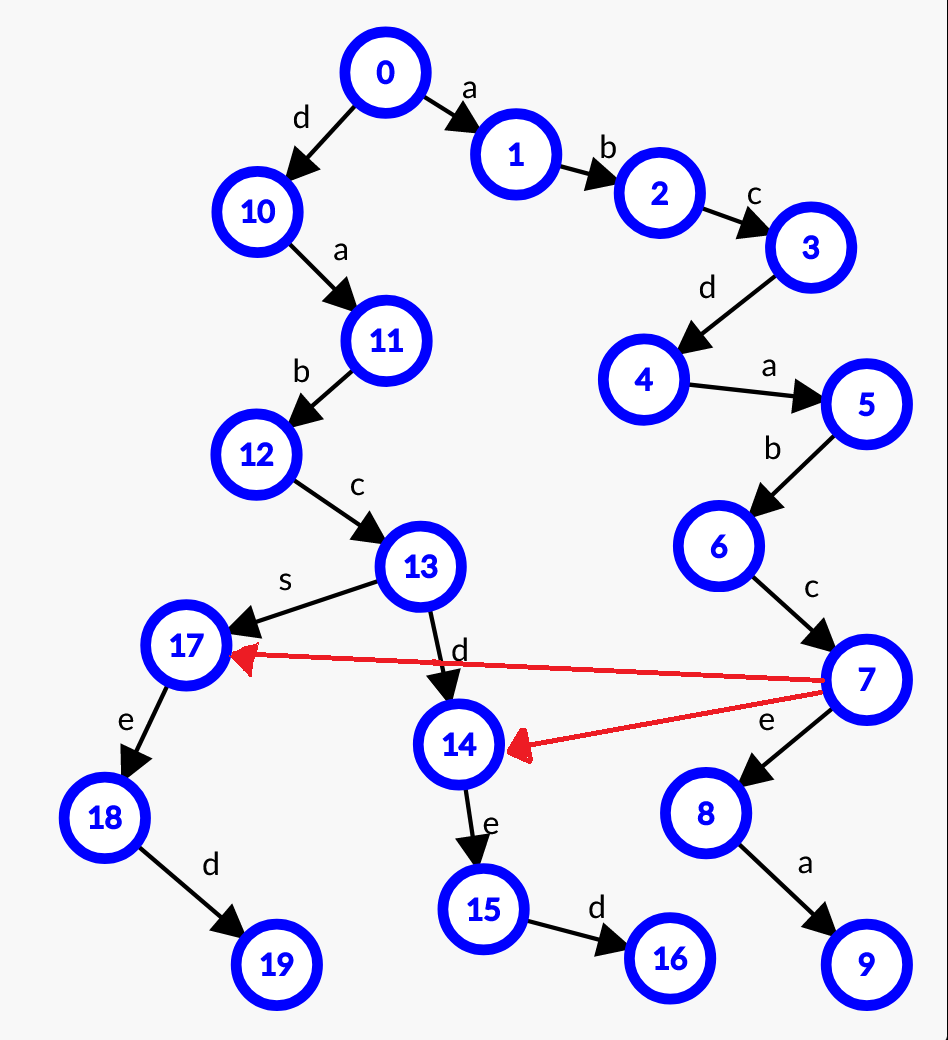
bfs 时，建立回跳边的过程详单与补充子节点，如果一个词的某个后继缺失，那我们通过建立回跳边进行补充，比如，我们用 \(ch[u][i]\) 表示节点 \(u\) 的下一个字符为 \(i\) 的儿子，如果 \(ch[u][i]=0\)，换言之，节点 \(u\) 没有这个儿子，那么，我们就将回跳边建在 \(ch[nxt[u]][i]\) 与节点 \(u\) 之间，即 \(ch[u][i]=ch[nxt[u]][i]\)，但是，我们还是需要记录 \(nxt[u]\) 的值的。

举个例子：在下述图片所示的 trie 树中：实际上，我们并没有真正的添加这些边而是对于没有的儿子进行了补充，例如，我们在 \(3\) 号和 \(8\) 之间建立了一条回跳边，但是并不是真正建立了这样一条边，而是，对于 \(3\) 号点没有的儿子进行了补充。

也就是说：在建完边之后，整个 trie 树将变成这个只可意会的样子（这甚至都有可能没画全）：

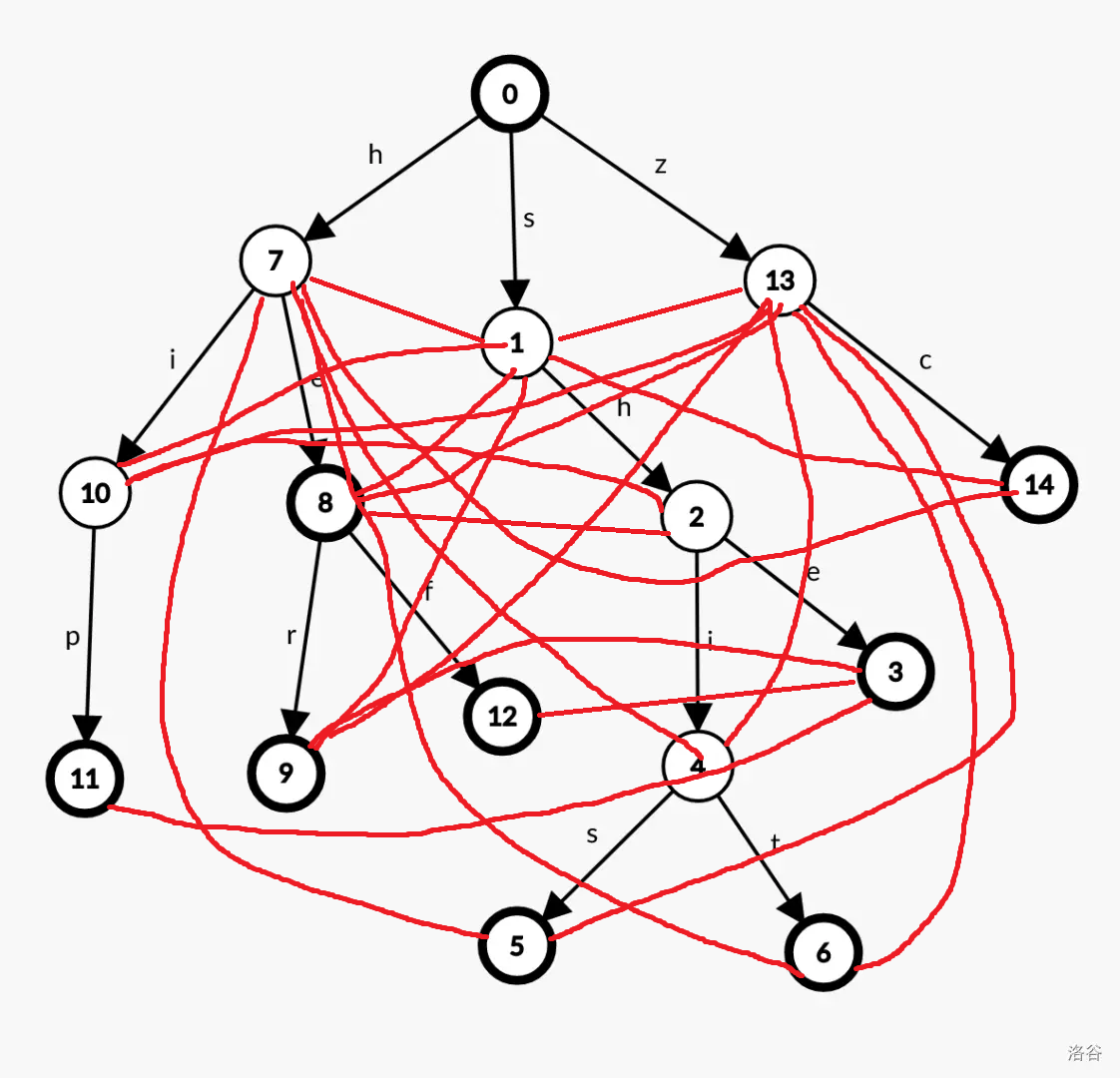
记录过的 nxt 数组就是下图和个样子（一条由 \(u\) 到 \(v\) 的从下向上的单项边就表示 \(nxt[u]=v\)）：

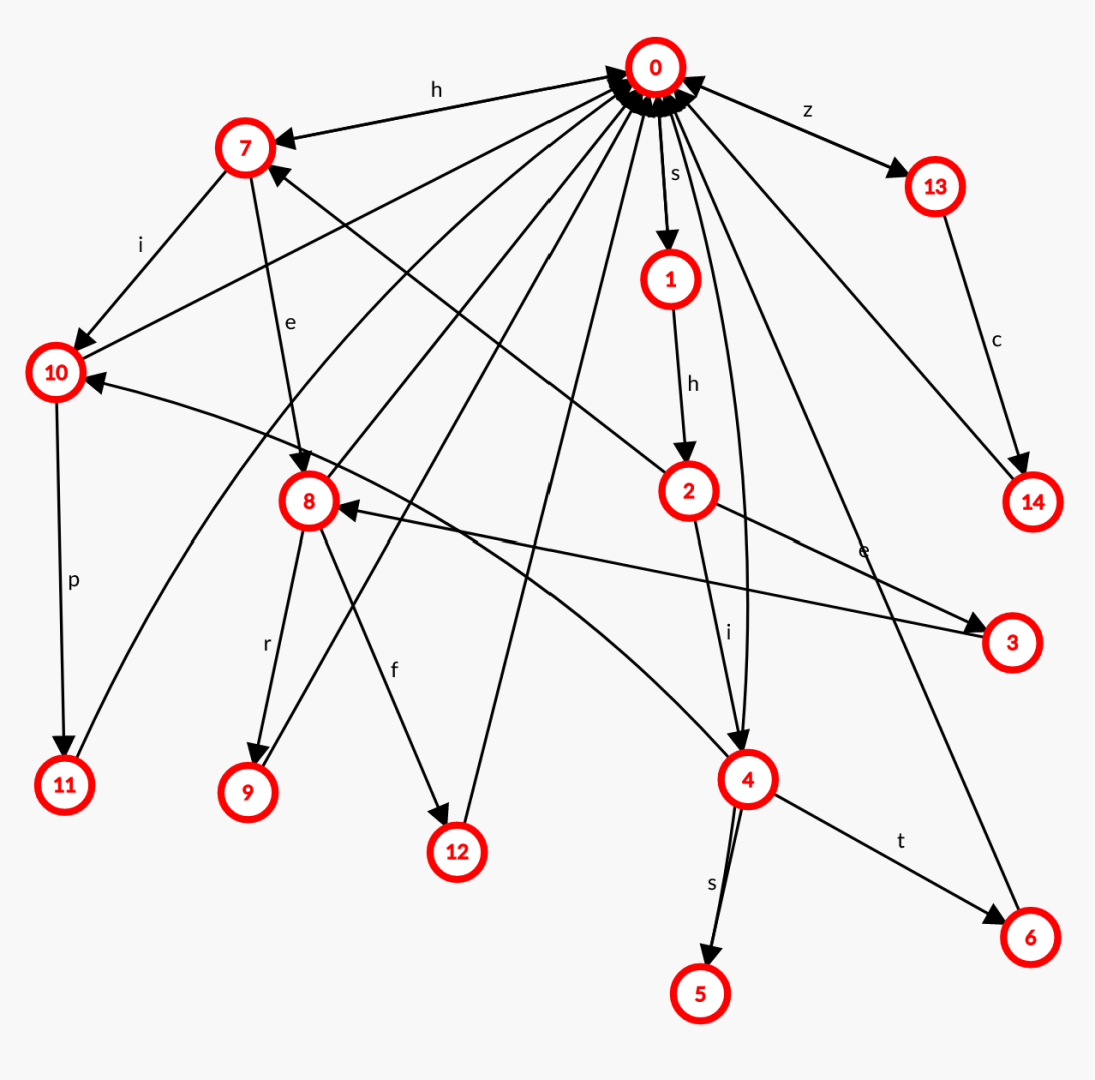
统计答案

对于一个给定的匹配串 \(S\)，找其中含有的给定字串，在朴素算法中，我们失配后就直接调回根节点重新匹配了，那么现在，当我们在节点 \(u\) 匹配到 \(s[j]\) 时，只需要跳到 \(ch[u][s[j+1]-\text{'a'}]\) 即可，实质上：如果原 trie 树中就有 \(ch[u][s[j+1]-\text{'a'}]\) 这条边，我们就是沿着转移边跳的，如果 \(ch[u][s[j+1]-\text{'a'}]\) 是我们后来建的回跳边，那么我们就相当于换了一个串进行匹配，如果没有 \(ch[u][s[j+1]-\text{'a'}]\) 这条边，那么 \(ch[u][s[j+1]-\text{'a'}]=0\)，我们就直接调回根节点直接匹配。

但是，当我们到达每个节点 \(u\) 时，就需要不仅统计其自身的 \(ed[u]\) 的值，而是需要从 \(u\) 往 \(nxt[u]\) 一直跳，递归统计每个能够跳到的点的 \(ed\) 值，这个过程很像链式前向星的做法，当我们已经统计过某个点的 \(ed\) 值之后，就不能重复统计了，所以我们把它设成 \(-1\)，当链式前向星在跳的时候，如果跳到了 \(ed[v]=-1\) 的点或者 \(v=0\)（也就是说跳回根节点了），就要停止跳跃。

以下是 AC 自动机的完整代码，各部分的具体意义在注释当中。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+3;
struct node {
	int ch[N][26];
	int tot,ed[N];
	int nxt[N];
	void insert(string s) {
		int cur=0;
		for(auto c:s) {
			if(!ch[cur][c-'a']) ch[cur][c-'a']=++tot;
			//动态开点
			cur=ch[cur][c-'a'];
		} ed[cur]++;
		//trie 树的常规添加字符串的操作
	}
	void build() {
		//通过 bfs 建立回跳边
		queue<int> q;
		for(int i=0;i<26;++i) if(ch[0][i]) q.push(ch[0][i]);
		while(q.size()){
			auto u=q.front();
			q.pop();
			for(int i=0;i<26;++i) {
				int v=ch[u][i];
				if(v) nxt[v]=ch[nxt[u]][i],q.push(v);
				//如果已经有一个可以继续往下前进的边，那么就继续往下前进，并将他的儿子加入队列
				else ch[u][i]=ch[nxt[u]][i];
				//否则直接建立回跳边
				//bfs 时相当于直接加边，实际破坏了 trie 树的结构，变成 trie 图
				//如果 nxt[u] 也没有 i 这个儿子，那么实际上回跳边就直接挂回了根节点
			}
		} //通过 bfs，我们就建立了回跳边
	}
	int find(string s) {
		//查询答案
		int cur=0,res=0;
		for(int i=0;i<s.size();++i) {
			char c=s[i];
			cur=ch[cur][c-'a'];
			//根据目标串进行跳跃
			int zc=cur;
			while(ed[zc]!=-1&&zc) {
				//如果统计到了根节点或者已经统计过的点，停止统计
				//前向星形式的统计答案
				res+=ed[zc];
				ed[zc]=-1;
				zc=nxt[zc];
				//为了避免统计答案重复，要求统计过后，将该点贡献设为 -1
			} //通过回跳边或者转移边跳到儿子节点
		} return res; //返回答案
	}
} trie;
void solve() {
	int n;
	cin>>n;
	for(int i=1;i<=n;++i) {
		string t;
		cin>>t;
		trie.insert(t);
	} trie.build();
	string s;
	cin>>s;
	cout<<trie.find(s)<<'\n';
	return;
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr),
	cout.tie(nullptr);
	solve();
	return 0;
}

提交链接：【模板】AC 自动机（简单版）。