Andrew NG 机器学习编程作业3 Octave

问题描述：使用逻辑回归(logistic regression)和神经网络(neural networks)识别手写的阿拉伯数字(0-9)

一、逻辑回归实现：

数据加载到octave中，如下图所示：

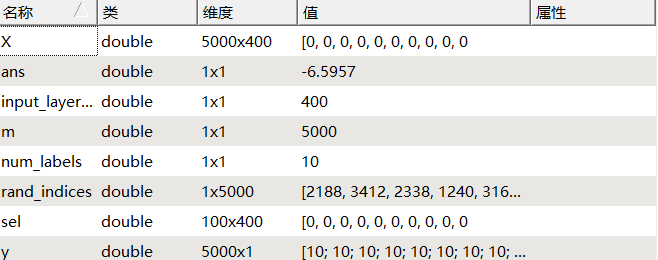
①样本数据的可视化

随机选择100个样本数据，使用Octave可视化的结果如下：

②使用逻辑回归来实现多分类问题(one-vs-all)

所谓多分类问题，是指分类的结果为三类以上。比如，预测明天的天气结果为三类：晴(用y==1表示)、阴(用y==2表示)、雨(用y==3表示)

分类的思想，其实与逻辑回归分类(默认是指二分类，binary classification)很相似，对“晴天”进行分类时，将另外两类(阴天和下雨)视为一类：(非晴天)，这样，就把一个多分类问题转化成了二分类问题。示意图如下：（图中的圆圈 表示：不属于某一类的 所有其他类）

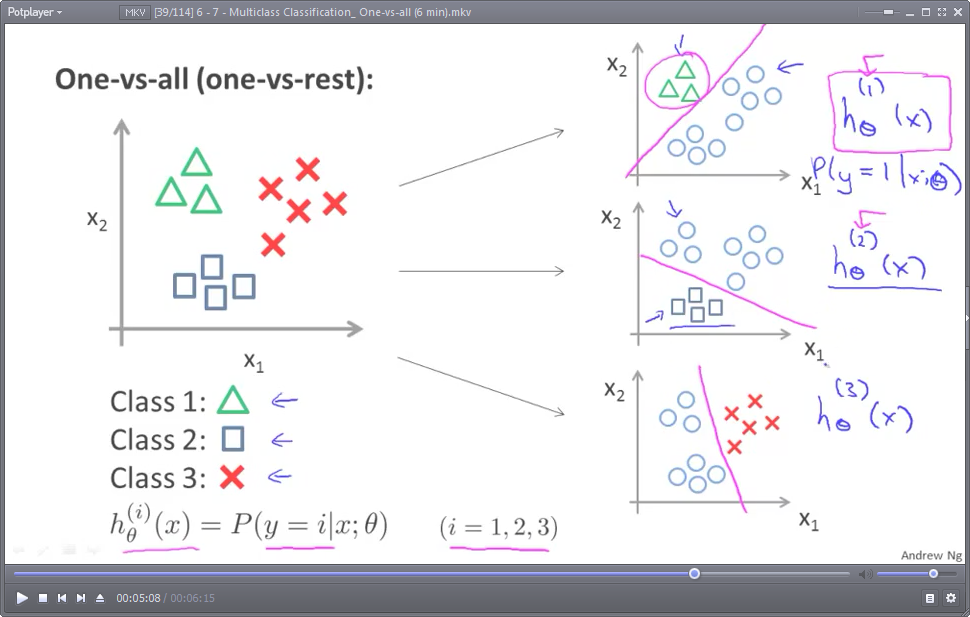
对于N分类问题(N>=3)，就需要N个假设函数(预测模型)，也即需要N组模型参数θ（θ一般是一个向量）

然后，对于每个样本实例，依次使用每个模型预测输出，选取输出值最大的那组模型所对应的预测结果作为最终结果。

因为模型的输出值，在sigmoid函数作用下，其实是一个概率值。，注意：h_θ⁽¹⁾(x)，h_θ⁽²⁾(x)，h_θ⁽³⁾(x)三组 模型参数θ 一般是不同的。比如：

h_θ⁽¹⁾(x)，输出 预测为晴天(y==1)的概率

h_θ⁽²⁾(x)，输出 预测为阴天(y==2)的概率

h_θ⁽³⁾(x)，输出 预测为雨天(y==3)的概率

 

③Octave代码实现 

对于上面的识别阿拉伯数字的问题，一共需要训练出10个逻辑回归模型，每个逻辑回归模型对应着识别其中一个数字。

我们一共有5000个样本，样本的预测结果值就是：y=(1,2,3,4,5,6,7,8,9,10)，其中 10 代表 数字0

我们使用fmincg库函数 来求解使得代价函数取最小值的 模型参数θ

function [all_theta] = oneVsAll(X, y, num_labels, lambda)
%ONEVSALL trains multiple logistic regression classifiers and returns all
%the classifiers in a matrix all_theta, where the i-th row of all_theta 
%corresponds to the classifier for label i
%   [all_theta] = ONEVSALL(X, y, num_labels, lambda) trains num_labels
%   logistic regression classifiers and returns each of these classifiers
%   in a matrix all_theta, where the i-th row of all_theta corresponds 
%   to the classifier for label i

% Some useful variables
m = size(X, 1);
n = size(X, 2);

% You need to return the following variables correctly 
all_theta = zeros(num_labels, n + 1);

% Add ones to the X data matrix
X = [ones(m, 1) X];

% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the following code to train num_labels
%               logistic regression classifiers with regularization
%               parameter lambda. 
%
% Hint: theta(:) will return a column vector.
%
% Hint: You can use y == c to obtain a vector of 1's and 0's that tell you
%       whether the ground truth is true/false for this class.
%
% Note: For this assignment, we recommend using fmincg to optimize the cost
%       function. It is okay to use a for-loop (for c = 1:num_labels) to
%       loop over the different classes.
%
%       fmincg works similarly to fminunc, but is more efficient when we
%       are dealing with large number of parameters.
%
% Example Code for fmincg:
%
%     % Set Initial theta
%     initial_theta = zeros(n + 1, 1);
%     
%     % Set options for fminunc
%     options = optimset('GradObj', 'on', 'MaxIter', 50);
% 
%     % Run fmincg to obtain the optimal theta
%     % This function will return theta and the cost 
%     [theta] = ...
%         fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
%                 initial_theta, options);
%


initial_theta = zeros(n + 1, 1);

options = optimset('GradObj','on','MaxIter',50);

for c = 1:num_labels %num_labels 为逻辑回归训练器的个数，num of logistic regression classifiers
all_theta(c, :) = fmincg(@(t)(lrCostFunction(t, X, (y == c),lambda)), initial_theta,options );
end









% =========================================================================


end

function [J, grad] = lrCostFunction(theta, X, y, lambda)
%LRCOSTFUNCTION Compute cost and gradient for logistic regression with 
%regularization
%   J = LRCOSTFUNCTION(theta, X, y, lambda) computes the cost of using
%   theta as the parameter for regularized logistic regression and the
%   gradient of the cost w.r.t. to the parameters. 

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
%
% Hint: The computation of the cost function and gradients can be
%       efficiently vectorized. For example, consider the computation
%
%           sigmoid(X * theta)
%
%       Each row of the resulting matrix will contain the value of the
%       prediction for that example. You can make use of this to vectorize
%       the cost function and gradient computations. 
%
% Hint: When computing the gradient of the regularized cost function, 
%       there're many possible vectorized solutions, but one solution
%       looks like:
%           grad = (unregularized gradient for logistic regression)
%           temp = theta; 
%           temp(1) = 0;   % because we don't add anything for j = 0  
%           grad = grad + YOUR_CODE_HERE (using the temp variable)
%

J = ( log( sigmoid(theta'*X') ) * y + log( 1-sigmoid(theta'*X') ) * (1 - y) )/(-m) + (lambda / (2*m)) * ( ( theta( 2:length(theta) ) )' * theta(2:length(theta)) );

grad = ( X' * ( sigmoid(X*theta)-y ) )/m + ( lambda / m ) * ( [0; ones( length(theta) - 1 , 1 )].*theta );








% =============================================================

grad = grad(:);

end

 

下面来解释一下 for循环：

num_labels 为分类器个数，共10个，每个分类器(模型)用来识别10个数字中的某一个。

我们一共有5000个样本，每个样本有400中特征变量，因此：模型参数θ 向量有401个元素。

initial_theta = zeros(n + 1, 1); % 模型参数θ的初始值(n == 400)

all_theta是一个10*401的矩阵，每一行存储着一个分类器(模型)的模型参数θ 向量，执行上面for循环，就调用fmincg库函数 求出了 所有模型的参数θ 向量了。

求出了每个模型的参数向量θ，就可以用 训练好的模型来识别数字了。对于一个给定的数字输入(400个 feature variables) input instance，每个模型的假设函数h_θ⁽ⁱ⁾(x) 输出一个值(i = 1,2,...10)。取这10个值中最大值那个值，作为最终的识别结果。比如g(h_θ⁽⁸⁾(x))==0.96 比其它所有的 g(h_θ⁽ⁱ⁾(x)) (i = 1,2,...10,但 i 不等于8) 都大，则识别的结果为 数字 8

 

function p = predictOneVsAll(all_theta, X)
%PREDICT Predict the label for a trained one-vs-all classifier. The labels 
%are in the range 1..K, where K = size(all_theta, 1). 
%  p = PREDICTONEVSALL(all_theta, X) will return a vector of predictions
%  for each example in the matrix X. Note that X contains the examples in
%  rows. all_theta is a matrix where the i-th row is a trained logistic
%  regression theta vector for the i-th class. You should set p to a vector
%  of values from 1..K (e.g., p = [1; 3; 1; 2] predicts classes 1, 3, 1, 2
%  for 4 examples) 

m = size(X, 1);
num_labels = size(all_theta, 1);

% You need to return the following variables correctly 
p = zeros(size(X, 1), 1);

% Add ones to the X data matrix
X = [ones(m, 1) X];

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned logistic regression parameters (one-vs-all).
%               You should set p to a vector of predictions (from 1 to
%               num_labels).
%
% Hint: This code can be done all vectorized using the max function.
%       In particular, the max function can also return the index of the 
%       max element, for more information see 'help max'. If your examples 
%       are in rows, then, you can use max(A, [], 2) to obtain the max 
%       for each row.
%       





[~,p] = max( X * all_theta',[],2); % 求矩阵(X*all_theta')每行的最大值，p 记录矩阵每行的最大值的索引

% =========================================================================


end

二、神经网络实现

由于逻辑回归是线性分类（它的假设函数是一个线性函数，就是划一条直线，把数据分成了两类。

对于一些复杂的类别，逻辑回归就解决不了了。比如下面这个图片中的分类。（无法通过 划直线 将 叉叉 和 圆圈 分开）

 

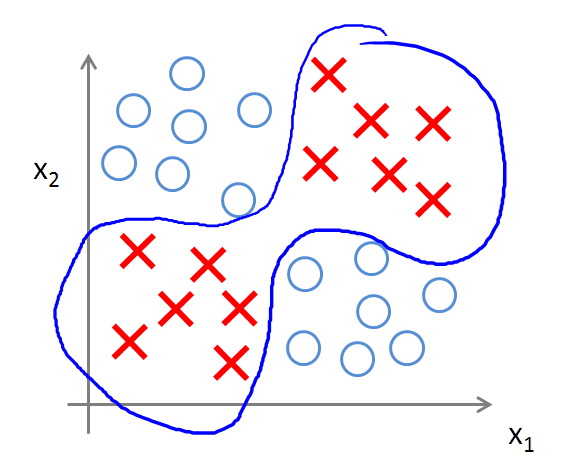
而神经网络，则能够实现很复杂的非线性分类问题。

对于神经网络而言，同样有一个训练样本矩阵 X，同时还有一个模型参数 Theta 矩阵，通过某种算法将 模型参数矩阵 训练好之后(求出 Theta 矩阵)，再使用前向传播算法( feedforward propagation algorithm)（感觉就像是矩阵相乘嘛）， 就可以对输入的测试样本进行预测了。

本作业中， 模型参数 Theta 矩阵是已经训练好了的，直接 load 即可。如下所示：

function p = predict(Theta1, Theta2, X)
%PREDICT Predict the label of an input given a trained neural network
%   p = PREDICT(Theta1, Theta2, X) outputs the predicted label of X given the
%   trained weights of a neural network (Theta1, Theta2)

% Useful values
m = size(X, 1);
num_labels = size(Theta2, 1);

% You need to return the following variables correctly 
p = zeros(size(X, 1), 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned neural network. You should set p to a 
%               vector containing labels between 1 to num_labels.
%
% Hint: The max function might come in useful. In particular, the max
%       function can also return the index of the max element, for more
%       information see 'help max'. If your examples are in rows, then, you
%       can use max(A, [], 2) to obtain the max for each row.
%



% 模拟实现前向传播算法
X = [ones(m, 1) X];
a_super_2 = sigmoid(Theta1 * X');
a_super_2 = [ones(1,m); a_super_2];% add bias unit
a_super_3 = sigmoid(Theta2 * a_super_2);
%==================================
[~,p] = max( a_super_3' ,[], 2 ); % 对样本的结果进行预测，与逻辑回归的预测类似，选取输出的最大值 作为最终的预测结果





% =========================================================================


end

 注意：我们正是通过 max 函数，求得矩阵 a_super3^′ 的每一行的最大值。将每一行的中的最大值 的索引 赋值给向量p。其中，a_super3^′ 是一个5000行乘10列的矩阵 

向量p就是预测的结果向量。而由于 a_super3^′ 有10列，故 p 中每个元素的取值范围为[1,10]，即分别代表了数字 0-9（其中10 表示 0）

测试代码如下：

 rp = randperm(m);
>>
>> for i = 1:m
    % Display
    fprintf('\nDisplaying Example Image\n');
    displayData(X(rp(i), :));

    pred = predict(Theta1, Theta2, X(rp(i),:));
    fprintf('\nNeural Network Prediction: %d (digit %d)\n', pred, mod(pred, 10));

    % Pause with quit option
    s = input('Paused - press enter to continue, q to exit:','s');
    if s == 'q'
      break
    end
end

例如下图所示的数字：