误差计算

目录

• Outline
• MSE
• Entropy
• Cross Entropy
• Binary Classification
  • Single output
• Classification
• Why not MSE？
• logits-->CrossEntropy

Outline

• MSE

• Cross Entropy Loss

• Hinge Loss

MSE

• loss=1N∑(y−out)2$loss=\frac{1}{N}\sum (y-out{)}^2$

• L2−norm=∑(y−out)−−−−−−−−−√$L_{2-norm}=\sqrt{\sum (y-out)}$

import tensorflow as tf

y = tf.constant([1, 2, 3, 0, 2])
y = tf.one_hot(y, depth=4)  # max_label=3种
y = tf.cast(y, dtype=tf.float32)
out = tf.random.normal([5, 4])

out

<tf.Tensor: id=117, shape=(5, 4), dtype=float32, numpy=
array([[ 0.8138832 , -1.1521571 ,  0.05197939,  2.3684442 ],
       [ 0.28827545, -0.35568208, -0.3952962 , -1.2576817 ],
       [-0.4354525 , -1.9914867 ,  0.37045303, -0.38287213],
       [-0.7680094 , -0.98293644,  0.62572837, -0.5673917 ],
       [ 1.5299634 ,  0.38036177, -0.28049606, -0.708137  ]],
      dtype=float32)>

loss1 = tf.reduce_mean(tf.square(y - out))
loss1

<tf.Tensor: id=122, shape=(), dtype=float32, numpy=1.5140966>

loss2 = tf.square(tf.norm(y - out)) / (5 * 4)
loss2

<tf.Tensor: id=99, shape=(), dtype=float32, numpy=1.3962512>

loss3 = tf.reduce_mean(tf.losses.MSE(y, out))
loss3

<tf.Tensor: id=105, shape=(), dtype=float32, numpy=1.3962513>

Entropy

• Uncertainty

• measure of surprise

• lower entropy --> more info.

Entropy=−∑iP(i)logP(i)$$\text{Entropy}=-\sum _{i}P(i)logP(i)$$

a = tf.fill([4], 0.25)
a * tf.math.log(a) / tf.math.log(2.)

<tf.Tensor: id=134, shape=(4,), dtype=float32, numpy=array([-0.5, -0.5, -0.5, -0.5], dtype=float32)>

-tf.reduce_sum(a * tf.math.log(a) / tf.math.log(2.))

<tf.Tensor: id=143, shape=(), dtype=float32, numpy=2.0>

a = tf.constant([0.1, 0.1, 0.1, 0.7])
-tf.reduce_sum(a * tf.math.log(a) / tf.math.log(2.))

<tf.Tensor: id=157, shape=(), dtype=float32, numpy=1.3567797>

a = tf.constant([0.01, 0.01, 0.01, 0.97])
-tf.reduce_sum(a * tf.math.log(a) / tf.math.log(2.))

<tf.Tensor: id=167, shape=(), dtype=float32, numpy=0.24194068>

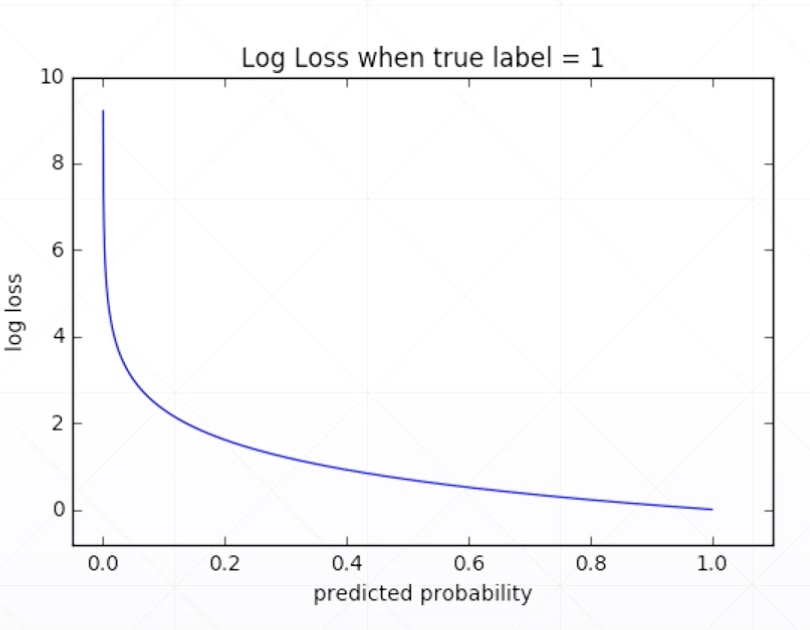
Cross Entropy

H(p,q)=−∑p(x)logq(x)H(p,q)=H(p)+DKL(p|q)$$\begin{gathered} H(p,q)=-\sum p(x)logq(x) \\ H(p,q)=H(p)+D_{KL}(p|q) \end{gathered}$$

• for p = q

  • Minima: H(p,q) = H(p)

• for P: one-hot encodint

  • h(p:[0,1,0])=−1log1=0$h(p:[0,1,0])=-1log1=0$
  • H([0,1,0],[p0,p1,p2])=0+DKL(p|q)=−1logq1$H([0,1,0],[p_0,p_1,p_2])=0+D_{KL}(p|q)=-1log{q}_1$ # p,q即真实值和预测值相等的话交叉熵为0

Binary Classification

• Two cases（第二种格式只需要输出一种情况，节省计算，无意义）

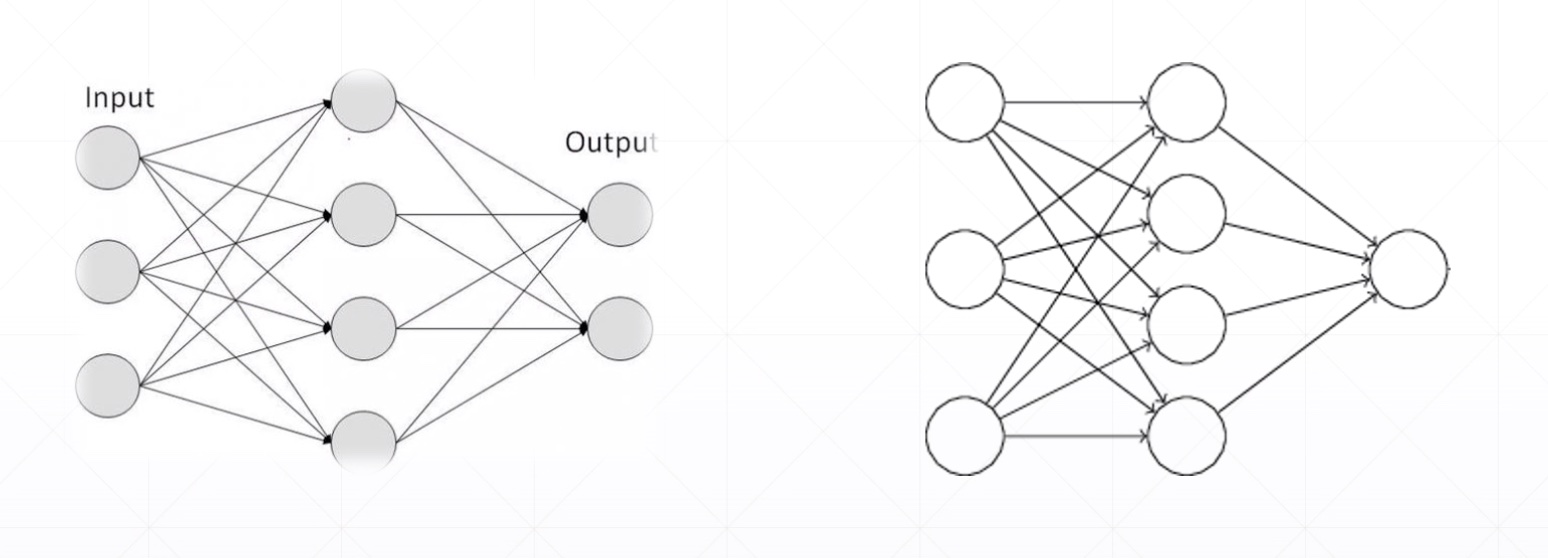
Single output

H(P,Q)=−P(cat)logQ(cat)−(1−P(cat))log(1−Q(cat))P(dog)=(1−P(cat))$$\begin{gathered} H(P,Q)=-P(cat)logQ(cat)-(1-P(cat))log(1-Q(cat)) \\ P(dog)=(1-P(cat)) \end{gathered}$$

H(P,Q)=−∑i=(cat,dog)P(i)logQ(i)=−P(cat)logQ(cat)−P(dog)logQ(dog)−(ylog(p)+(1−y)log(1−p))$$\begin{array}{rl}H(P,Q)& =-\sum _{i=(cat,dog)}P(i)logQ(i)\\ & =-P(cat)logQ(cat)-P(dog)logQ(dog)-(ylog(p)+(1-y)log(1-p))\end{array}$$

Classification

• H([0,1,0],[p0,p1,p2])=0+DKL(p|q)=−1logq1$H([0,1,0],[p_0,p_1,p_2])=0+D_{KL}(p|q)=-1log{q}_1$

P1=[1,0,0,0,0]Q1=[0.4,0.3,0.05,0.05,0.2]$$\begin{array}{rl}& P_1=[1,0,0,0,0]\\ & Q_1=[0.4,0.3,0.05,0.05,0.2]\end{array}$$

H(P1,Q1)=−∑P1(i)logQ1(i)=−(1log0.4+0log0.3+0log0.05+0log0.05+0log0.2)=−log0.4≈0.916$$\begin{array}{rl}H(P_1,Q_1)& =-\sum P_1(i)log{Q}_1(i)\\ & =-(1log0.4+0log0.3+0log0.05+0log0.05+0log0.2)\\ & =-log0.4\\ & \approx 0.916\end{array}$$

P1=[1,0,0,0,0]Q1=[0.98,0.01,0,0,0.01]$$\begin{array}{rl}& P_1=[1,0,0,0,0]\\ & Q_1=[0.98,0.01,0,0,0.01]\end{array}$$

H(P1,Q1)=−∑P1(i)logQ1(i)=−log0.98≈0.02$$\begin{array}{rl}H(P_1,Q_1)& =-\sum P_1(i)log{Q}_1(i)\\ & =-log0.98\\ & \approx 0.02\end{array}$$

tf.losses.categorical_crossentropy([0, 1, 0, 0], [0.25, 0.25, 0.25, 0.25])

<tf.Tensor: id=186, shape=(), dtype=float32, numpy=1.3862944>

tf.losses.categorical_crossentropy([0, 1, 0, 0], [0.1, 0.1, 0.8, 0.1])

<tf.Tensor: id=205, shape=(), dtype=float32, numpy=2.3978953>

tf.losses.categorical_crossentropy([0, 1, 0, 0], [0.1, 0.7, 0.1, 0.1])

<tf.Tensor: id=243, shape=(), dtype=float32, numpy=0.35667497>

tf.losses.categorical_crossentropy([0, 1, 0, 0], [0.01, 0.97, 0.01, 0.01])

<tf.Tensor: id=262, shape=(), dtype=float32, numpy=0.030459179>

tf.losses.BinaryCrossentropy()([1],[0.1])

<tf.Tensor: id=306, shape=(), dtype=float32, numpy=2.3025842>

tf.losses.binary_crossentropy([1],[0.1])

<tf.Tensor: id=333, shape=(), dtype=float32, numpy=2.3025842>

Why not MSE？

• sigmoid + MSE

  • gradient vanish

• converge slower

• However

  • e.g. meta-learning

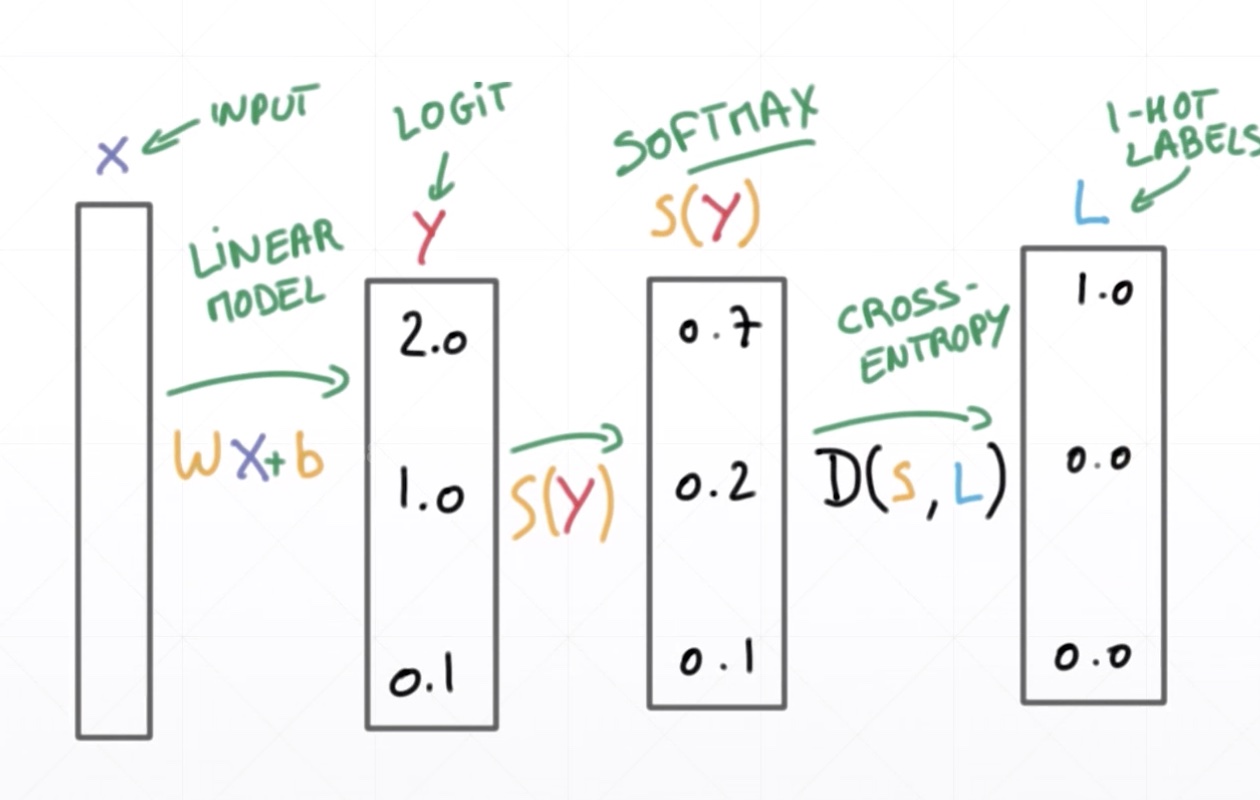
logits-->CrossEntropy