决策树学习是应用最广的归纳推理算法之一,是一种逼近离散值函数的方法,主要的算法有:ID3算法、C4.5算法及CART。
在机器学习中,决策树是一种预测模型,代表的是一种对象属性与对象值之间的一种映射关系,每一个节点代表某个对象,树中的每一个分叉路径代表某个可能的属性值,而每一个叶子节点则对应从根节点到该叶子节点所经历的路径所表示的对象的值。决策树仅有单一输出,如果有多个输出,可以分别建立独立的决策树以处理不同的输出。
适用的特征:
实例由“属性-值”对表示
目标函数具有离散的输出值
训练数据可以包含错误
训练数据可以包含缺少属性值的实例
ID3算法介绍
ID3算法是决策树的一种,它是基于奥卡姆剃刀原理的,即用尽量用较少的东西做更多的事。ID3算法,即Iterative Dichotomiser 3,迭代二叉树3代,是Ross Quinlan发明的一种决策树算法,这个算法的基础就是上面提到的奥卡姆剃刀原理,越是小型的决策树越优于大的决策树,尽管如此,也不总是生成最小的树型结构,而是一个启发式算法。
在信息论中,期望信息越小,那么信息增益就越大,从而纯度就越高。ID3算法的核心思想就是以信息增益来度量属性的选择,选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍历可能的决策空间。
3. 信息熵与信息增益
在信息增益中,重要性的衡量标准就是看特征能够为分类系统带来多少信息,带来的信息越多,该特征越重要。在认识信息增益之前,先来看看信息熵的定义
熵这个概念最早起源于物理学,在物理学中是用来度量一个热力学系统的无序程度,而在信息学里面,熵是对不确定性的度量。在1948年,香农引入了信息熵,将其定义为离散随机事件出现的概率,一个系统越是有序,信息熵就越低,反之一个系统越是混乱,它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。
假如一个随机变量 的取值为
的取值为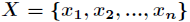 ,每一种取到的概率分别是
,每一种取到的概率分别是 ,那么
,那么
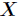 的熵定义为
的熵定义为
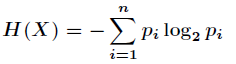
意思是一个变量的变化情况可能越多,那么它携带的信息量就越大。
对于分类系统来说,类别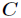 是变量,它的取值是
是变量,它的取值是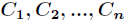 ,而每一个类别出现的概率分别是
,而每一个类别出现的概率分别是
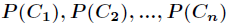
而这里的 就是类别的总数,此时分类系统的熵就可以表示为
就是类别的总数,此时分类系统的熵就可以表示为
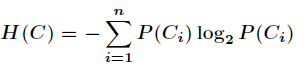
以上就是信息熵的定义,接下来介绍信息增益。
信息增益是针对一个一个特征而言的,就是看一个特征 ,系统有它和没有它时的信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即信息增益。
,系统有它和没有它时的信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即信息增益。
接下来以天气预报的例子来说明。下面是描述天气数据表,学习目标是play或者not play。
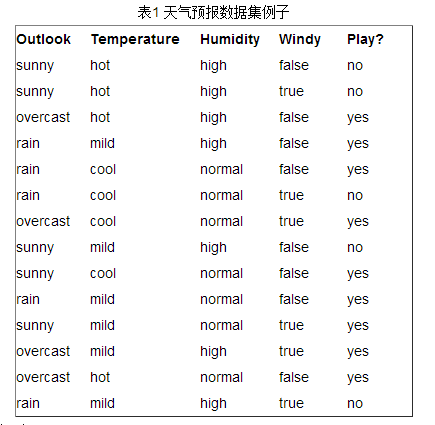
可以看出,一共14个样例,包括9个正例和5个负例。那么当前信息的熵计算如下

在决策树分类问题中,信息增益就是决策树在进行属性选择划分前和划分后信息的差值。假设利用
属性Outlook来分类,那么如下图
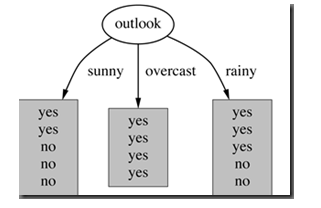
划分后,数据被分为三部分了,那么各个分支的信息熵计算如下

那么划分后的信息熵为
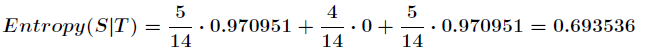
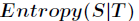 代表在特征属性
代表在特征属性 的条件下样本的条件熵。那么最终得到特征属性
的条件下样本的条件熵。那么最终得到特征属性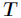 带来的信息增益为
带来的信息增益为
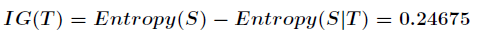
信息增益的计算公式如下
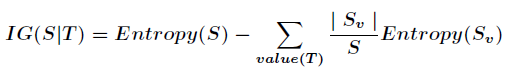
其中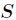 为全部样本集合,
为全部样本集合,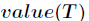 是属性
是属性 所有取值的集合,
所有取值的集合, 是
是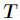 的其中一个属性值,
的其中一个属性值,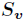 是
是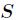 中属性
中属性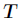 的值为
的值为 的样例集合,
的样例集合,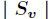 为
为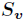 中所含样例数。
中所含样例数。
在决策树的每一个非叶子结点划分之前,先计算每一个属性所带来的信息增益,选择最大信息增益的属性来划分,因为信息增益越大,区分样本的能力就越强,越具有代表性,很显然这是一种自顶向下的贪心策略。以上就是ID3算法的核心思想。
ID3的优缺点:
优点:
假设空间包含所有的决策树,它是关于现有属性的有限离散值函数的一个完整空间,避免搜索不完整假设空间的一个主要风险:假设空间可能不包含目标函数。
在搜索的每一步都使用当前的所有训练样例,不同于基于单独的训练样例递增作出决定,容错性增强。
在搜索过程中不进行回溯,可能收敛到局部最优而不是全局最优。
只能处理离散值的属性,不能处理连续值的属性。信息增益度量存在一个内在偏置,它偏袒具有较多值的属性。
C4.5算法
C4.5 算法继承了ID3 算法的优点,并在以下几方面对ID3 算法进行了改进:
增益比率度量是用前面的增益度量Gain(S,A)和分裂信息度量SplitInformation(S,A)来共同定义的,如下所示:
其中,分裂信息度量被定义为(分裂信息用来衡量属性分裂数据的广度和均匀):
其中S1到Sc是c个值的属性A分割S而形成的c个样例子集。注意分裂信息实际上就是S关于属性A的各值的熵。
C4.5算法构造决策树的过程
- Function C4.5(R:包含连续属性的无类别属性集合,C:类别属性,S:训练集)
- Begin
- If S为空,返回一个值为Failure的单个节点;
- If S是由相同类别属性值的记录组成,
- 返回一个带有该值的单个节点;
- If R为空,则返回一个单节点,其值为在S的记录中找出的频率最高的类别属性值;
- [注意未出现错误则意味着是不适合分类的记录];
- For 所有的属性R(Ri) Do
- If 属性Ri为连续属性,则
- Begin
- 将Ri的最小值赋给A1:
- 将Rm的最大值赋给Am;
- For j From 2 To m-1 Do Aj=A1+j*(A1Am)/m;
- 将Ri点的基于{< =Aj,>Aj}的最大信息增益属性(Ri,S)赋给A;
- End;
- 将R中属性之间具有最大信息增益的属性(D,S)赋给D;
- 将属性D的值赋给{dj/j=1,2...m};
- 将分别由对应于D的值为dj的记录组成的S的子集赋给{sj/j=1,2...m};
- 返回一棵树,其根标记为D;树枝标记为d1,d2...dm;
- 再分别构造以下树:
- C4.5(R-{D},C,S1),C4.5(R-{D},C,S2)...C4.5(R-{D},C,Sm);
- End C4.5
CART算法
使用基尼指数进行属性选择, 请参阅 https://blog.csdn.net/gzj_1101/article/details/78355234



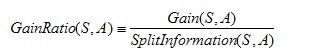
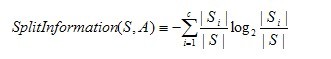

 浙公网安备 33010602011771号
浙公网安备 33010602011771号