一个简单不等式的证明（旧文补完）
\[x\ln\dfrac{x}{x-1}>1,\quad\forall x>1.
\]
该不等式曾出现于无旋平衡树（范浩强 Treap）平均时间复杂度证明的一步放缩，但原文并未给出证明. 现将其补完.
实际上，这只是一道很简单的高中导数题罢了.
证明
熟知 \(\ln\) 的切线不等式
\[\ln t<t-1,\quad\forall t\in(0,1)\cup(1,+\infty).
\]
令 \(t=\dfrac{x-1}x\ (x>1)\) 得
\[\ln\dfrac{x-1}x<-\dfrac1x.
\]
两边同乘 \(-x\) 得
\[x\ln\dfrac{x}{x-1}>1.
\]
这便是所要证的.
笔者还想继续讨论该式的更多性质.
令
\[f(x)=x\ln\dfrac{x}{x-1},\quad x\in(1,+\infty).
\]
\(f(x)\) 的单调性
\[f'(x)=\ln\dfrac x{x-1}-\dfrac1{x-1}.
\]
在切线不等式中令 \(u=\dfrac{x}{x-1}\ (x>1)\) 得
\[\ln\dfrac{x}{x-1}<\dfrac{x}{x-1}-1=\dfrac1{x-1}.
\]
故 \(f'(x)<0\)，\(f(x)\) 在定义域上单调减少.
\(f(x)\) 的凹凸性
\[\begin{align*}
f''(x)&=\dfrac1x-\dfrac1{x-1}+\dfrac1{(x-1)^2}
\\&=\dfrac1{x(x-1)^2}>0.
\end{align*}
\]
因此 \(f(x)\) 是凸函数.
\(f(x)\) 的渐进线
当 \(x\rightarrow1^+\) 时，\(\dfrac{x}{x-1}\rightarrow+\infty\)，故 \(f(x)\rightarrow+\infty\).
当 \(x\rightarrow+\infty\) 时，\(x\ln\dfrac{x}{x-1}=\ln\left(1+\dfrac1{-x}\right)^{-x}\rightarrow\ln\mathrm{e}=1\). 这一步极限是“两个重要极限”之一.
因此 \(f(x)\) 有渐近线 \(x=1\) 和 \(y=1\). 结合单调性可知，其图象在两条渐近线的右上方.
\(f(x)\) 的图象
基于以上讨论，容易作出函数的图象：
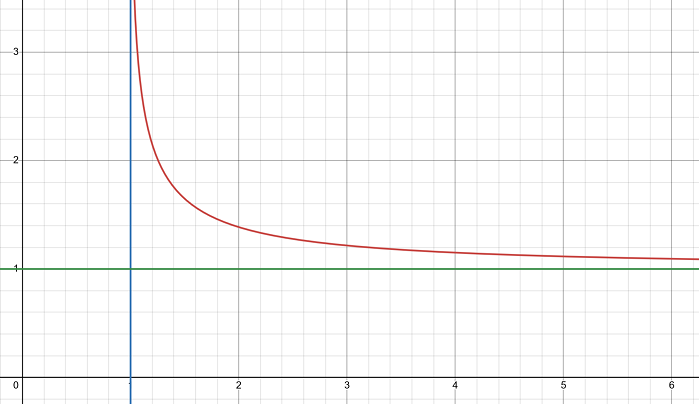
\(f(x)\) 的渐近行为
此处研究 \(x\rightarrow+\infty\) 时 \(f(x)\rightarrow1\) 的速度. 下面证明 \(f(x)-1\sim \dfrac{1}{2x}\)，即 \(f(x)-1\) 与 \(\dfrac1{2x}\) 是等价无穷小.
直接作比，用两次洛必达法则（显然有 \(f'(x)\rightarrow0\)）：
\[\begin{align*}
\lim_{x\rightarrow+\infty}\dfrac{f(x)-1}{(2x)^{-1}}
&=\lim_{x\rightarrow+\infty}\dfrac{f'(x)}{-2^{-1}x^{-2}}
\\&=\lim_{x\rightarrow+\infty}\dfrac{f''(x)}{x^{-3}}
\\&=\lim_{x\rightarrow+\infty}\dfrac{x^{-1}(x-1)^{-2}}{x^{-3}}
\\&=\lim_{x\rightarrow+\infty}\left(\dfrac{x}{x-1}\right)^2
\\&=\lim_{x\rightarrow+\infty}\left(1+\dfrac1{x-1}\right)^2
\\&=1.
\end{align*}
\]
