详解使用 Tarjan 求 LCA 问题(图解)
LCA问题有多种求法,例如倍增,Tarjan。
本篇博文讲解如何使用Tarjan求LCA。
如果你还不知道什么是LCA,没关系,本文会详细解释。
在本文中,因为我懒为方便理解,使用二叉树进行示范。
LCA是什么,能吃吗?
LCA是树上最近公共祖先问题。
最近公共祖先就是树上有两个结点,找一个结点,是他们的公共祖先,并且离他们两个结点最近。
例如这是一棵树:
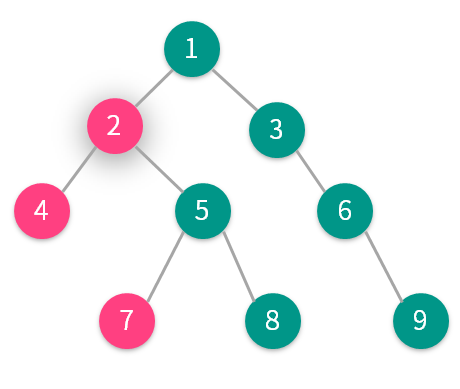
树上 4,7 两个结点的 LCA 就是 2 了。
1 虽然也是他们的公共祖先,但并不是最近的。
再举个例子,8,5 的祖先是 5。8,6 的祖先是 1。
怎么求LCA问题?
在开头已经说过了,LCA 问题有多种求法。本文要介绍的是相对简单的 Tarjan 求 LCA。
注意:Tarjan 求 LCA 是一种离线的算法,也就是说它一遍求出所有需要求的点的 LCA,而不是需要求哪两个点再去求。
在开始介绍前的补充
Tarjan 求 LCA 需要用到并查集,以下是本人使用的并查集模板。
1 2 3 4 5 6 7 8 9 10 11 12 | int fa[100000];void reset(){ for (int i=1;i<=100000;i++){ fa[i]=i; }}int getfa(int x){ return fa[x]==x?x:getfa(fa[x]);}void marge(int x,int y){ fa[getfa(y)]=getfa(x);} |
由于 Tarjan 是在遍历到目标点的时候得出答案并输出,那么如果你不输出,就需要使用一些东西来记录它(一般不用)。
关于记录
除非你之后需要 LCA 的结果再做一些操作,否则不需要记录,直接在 DFS 中输出即可。
我使用的是 STL 中的 Map 和 Pair,因为 LCA 是求两个点,Pair 正好可以满足一对数据。而 Map 的哈希机制可以实现 O(1) 查找。
Tarjan 求 LCA 做法
总体思想
遍历每一个结点并使用并查集记录父子关系。
Tarjan 是一种 DFS 的思想。我们需要从根结点去遍历这棵树。
当遍历到某一个结点(称之为 x) 时,你有以下几点需要做的。
1将当前结点标记为已经访问。
2递归遍历所有它的子节点(称之为 y),并在递归执行完后用并查集合并 x 和 y。
3遍历与当前节点有查询关系的结点(称之为 z)(即是需要查询 LCA 的另一些结点),如果 z 已经访问,那么 x 与 z 的 LCA 就是 (这个是并查集中的查找函数),输出或者记录下来就可以了。
这是伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 | void tarjan(int x){ //在本代码段中,s[i]为第i个子节点 , t[i]为第i个和当前节点有查询关系的结点。 vis[x]=1;//标记已经访问,vis是记录是否已访问的数组 for (i=1;i<=子节点数;i++){//枚举子节点 (递归并合并) tarjan(s[i]); marge(x,s[i]);//并查集合并 } for (i=1;i<=有查询关系的结点数;i++){ if (vis[t[i]]){ cout<<x<<"和"<<t[i]<<"的LCA是"<<getfa(t[i])<<endl;//如果t[i]已经访问了输出(getfa是并查集查找函数) } }} |
核心代码就这么一点?对,就这么一点。
如果你还不理解,那么可以跳转到最后一章看图解演示。
一些重要的细节
为了接下来的讲解,下面我们明确一下读入方式,不同的读入方式可以自己变通一下。
第一行两个数 n 和 q,表示结点数和查询数。
接下来 n 行每行两个数,表示左子结点和右子结点编号,如没有则是 -1。
接下来 q 行每行两个数,表示查询的两个结点编号。
例如上图的树,读入为
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 9 52 34 5-1 6-1 -17 8 -1 9-1 -1-1 -1-1 -15 47 47 89 38 6 |
如何存储查询关系
我在这里用的方法是二维数组。
int t[100000][10],top[100000];//t[i][j]表示编号为i的结点,第j个和它有查询关系的点的编号//top[i]表示编号为i的结点与它有查询关系的点的数量 |
注意:需要双向存储关系。例如结点 2 和 3,不仅要更新t[2],还要更新t[3]。
读入代码长这样:
1 2 3 4 5 | for (int i=1;i<=q;i++){ cin>>a[i]>>b[i]; t[a[i]][++top[a[i]]]=b[i]; t[b[i]][++top[b[i]]]=a[i];} |
当然如果你想要优化下空间那么把这个数组变成vector也是没问题的。
这就没了...
代码
直接输出的写法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | #include<bits/stdc++.h>using namespace std;int n,k,q,v[100000];map<pair<int,int>,int> ans;//存答案 int t[100000][10],top[100000];//存储查询关系struct node{ int l,r;};node s[100000];/*并查集*/int fa[100000];void reset(){ for (int i=1;i<=n;i++){ fa[i]=i; }}int getfa(int x){ return fa[x]==x?x:getfa(fa[x]);}void marge(int x,int y){ fa[getfa(y)]=getfa(x);}/*------*/void tarjan(int x){ v[x]=1;//标记已访问 node p=s[x];//获取当前结点结构体 if (p.l!=-1){ tarjan(p.l); marge(x,p.l); } if (p.r!=-1){ tarjan(p.r); marge(x,p.r); }//分别对l和r结点进行操作 for (int i=1;i<=top[x];i++){ if (v[t[x][i]]){ cout<<getfa(t[x][i])<<endl; }//输出 }}int main(){ cin>>n>>q; for (int i=1;i<=n;i++){ cin>>s[i].l>>s[i].r; } for (int i=1;i<=q;i++){ int a,b; cin>>a>>b; t[a][++top[a]]=b;//存储查询关系 t[b][++top[b]]=a; } reset();//初始化并查集 tarjan(1);//tarjan 求 LCA} |
先记录而不输出的写法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 | #include<bits/stdc++.h>using namespace std;int n,k,q,v[100000];map<pair<int,int>,int> ans;//存答案 int t[100000][10],top[100000];//存储查询关系int a[100000],b[100000];struct node{ int l,r;};node s[100000];/*并查集*/int fa[100000];void reset(){ for (int i=1;i<=n;i++){ fa[i]=i; }}int getfa(int x){ return fa[x]==x?x:getfa(fa[x]);}void marge(int x,int y){ fa[getfa(y)]=getfa(x);}/*------*/void tarjan(int x){ v[x]=1; node p=s[x]; if (p.l!=-1){ tarjan(p.l); marge(x,p.l); } if (p.r!=-1){ tarjan(p.r); marge(x,p.r); } for (int i=1;i<=top[x];i++){ if (v[t[x][i]]){ pair<int,int> tmp,tmp1;//用pair配合map来存储答案 tmp=make_pair(x,t[x][i]); tmp1=make_pair(t[x][i],x);//两个pair的目的是例如3 2这种数据如果搜到3才有答案那么进时的顺序不止是(3,2),还有(2,3),方便输出结果时查询 ans[tmp]=getfa(t[x][i]); ans[tmp1]=getfa(t[x][i]); cout<<"#"<<ans[tmp]<<endl; } }}int main(){ cin>>n>>q; for (int i=1;i<=n;i++){ cin>>s[i].l>>s[i].r; } for (int i=1;i<=q;i++){ cin>>a[i]>>b[i]; t[a[i]][++top[a[i]]]=b[i]; t[b[i]][++top[b[i]]]=a[i]; } reset(); tarjan(1); for (int i=1;i<=q;i++){ pair<int,int> tmp; tmp=make_pair(b[i],a[i]); cout<<a[i]<<"-"<<b[i]<<":"<<ans[tmp]<<endl; }} |
算法演示
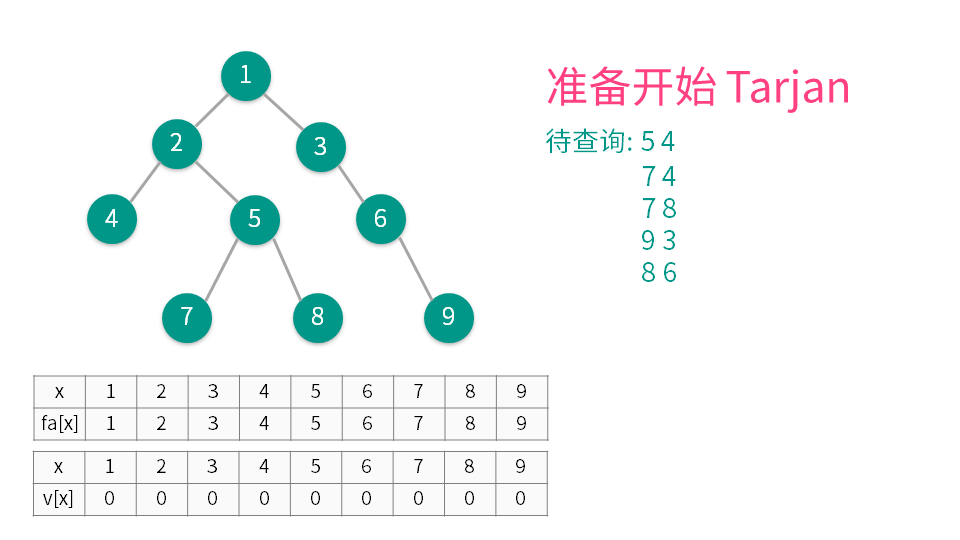


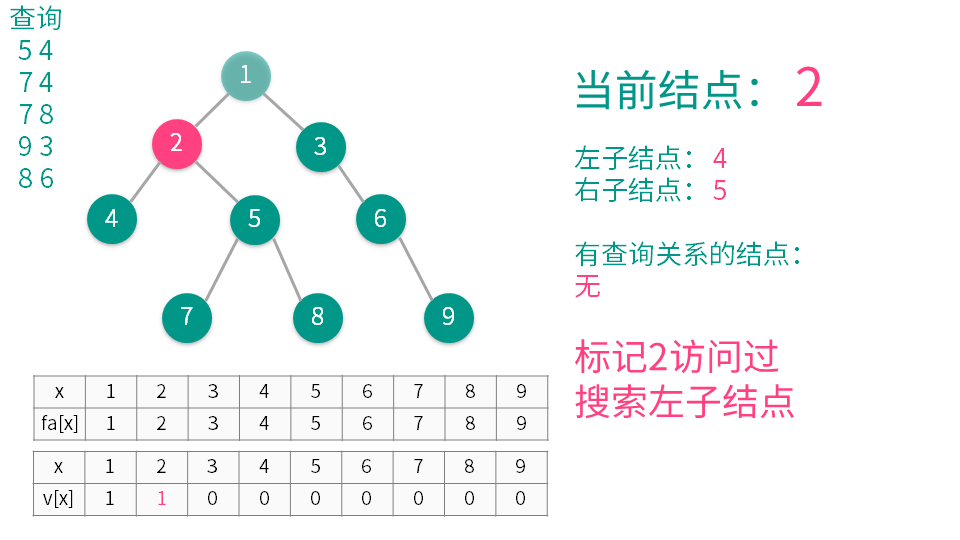
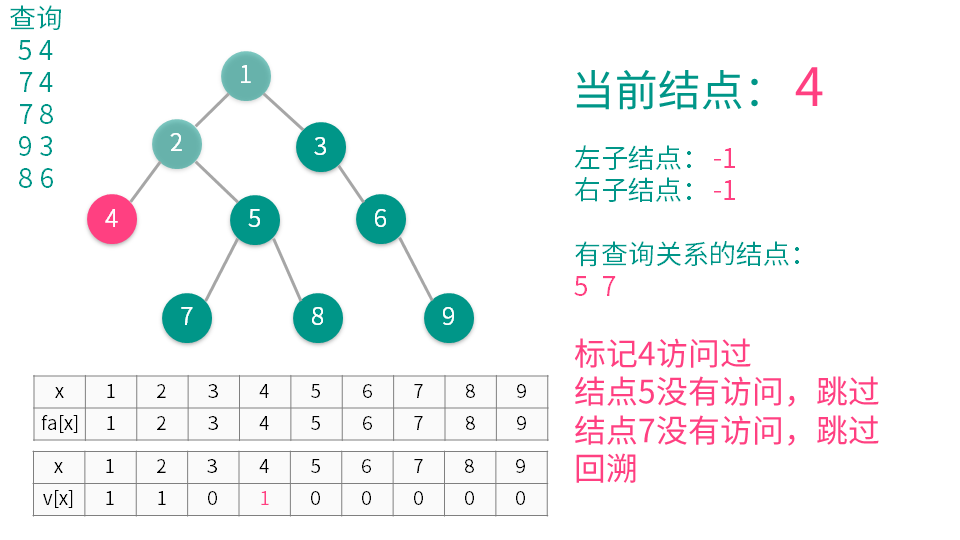

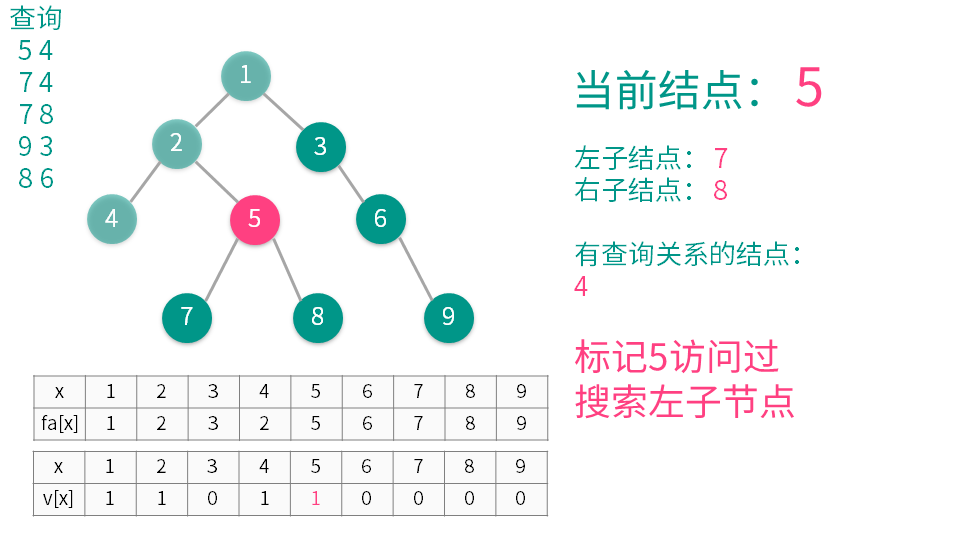
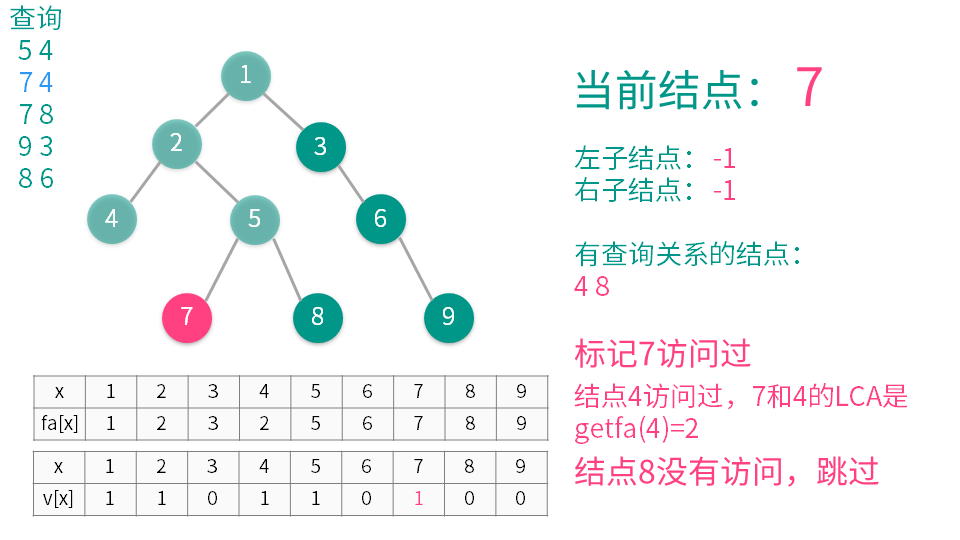

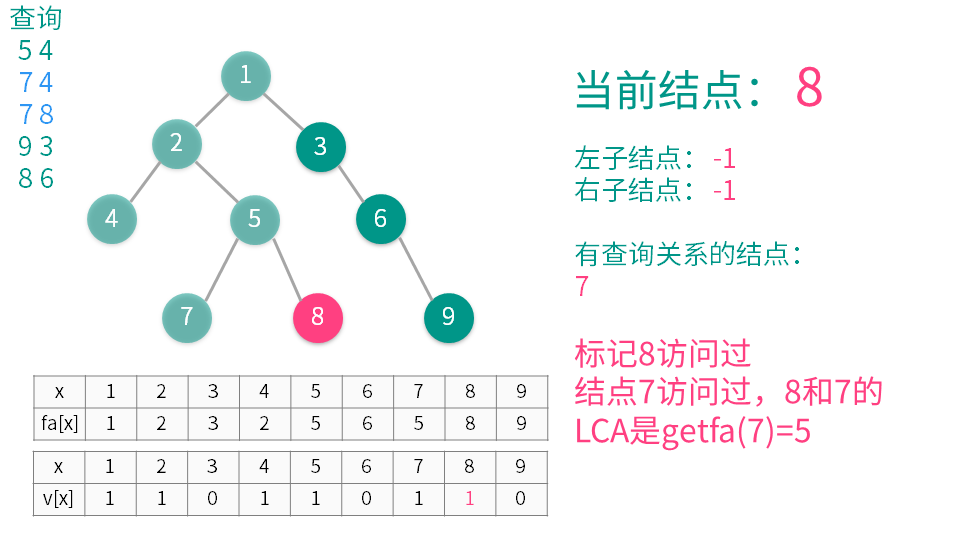

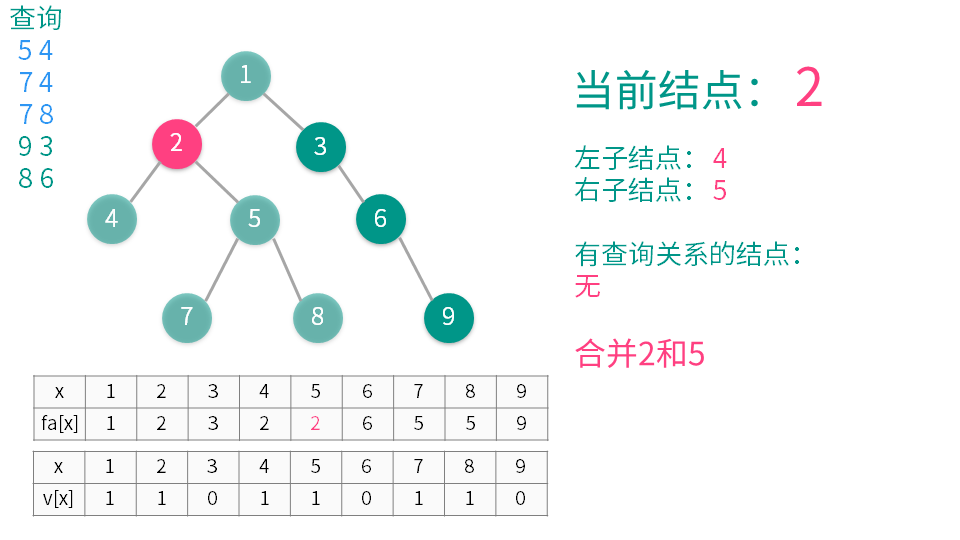
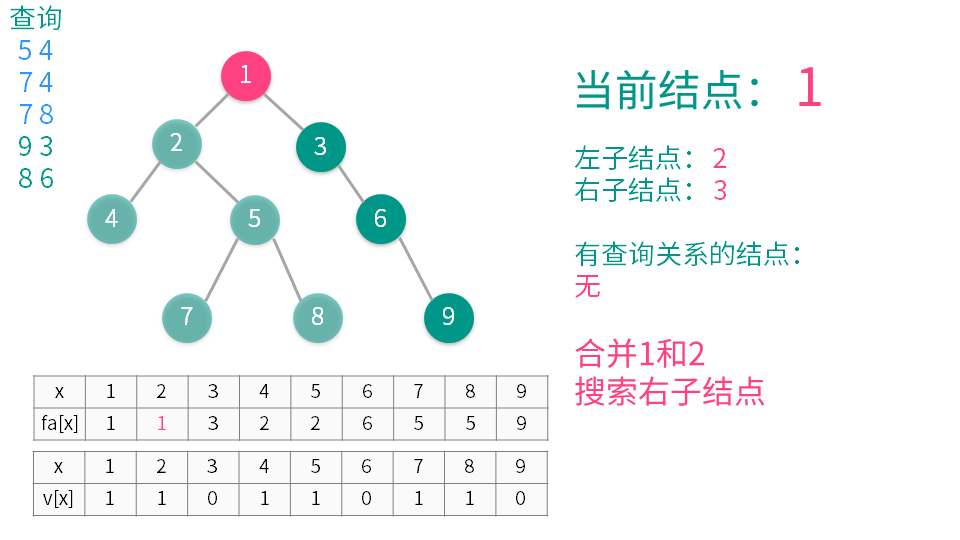
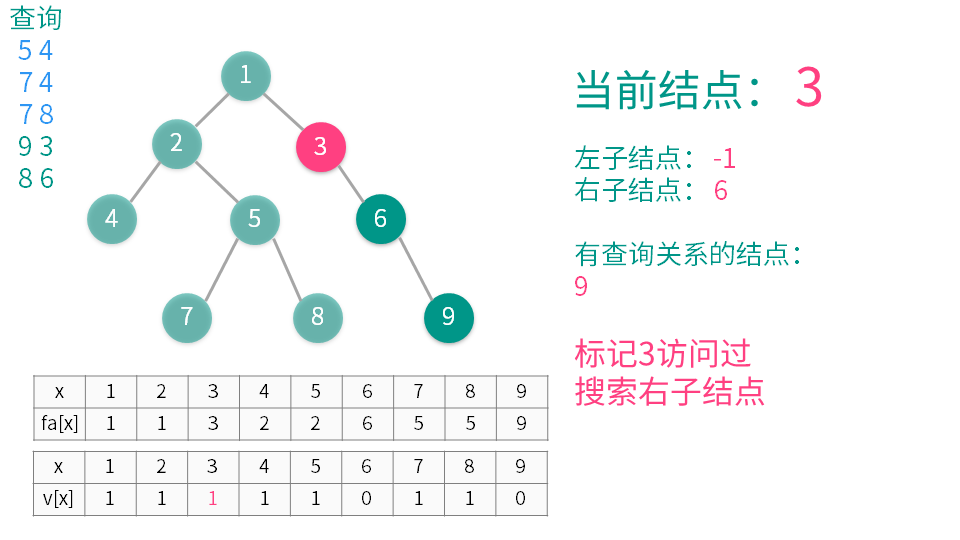
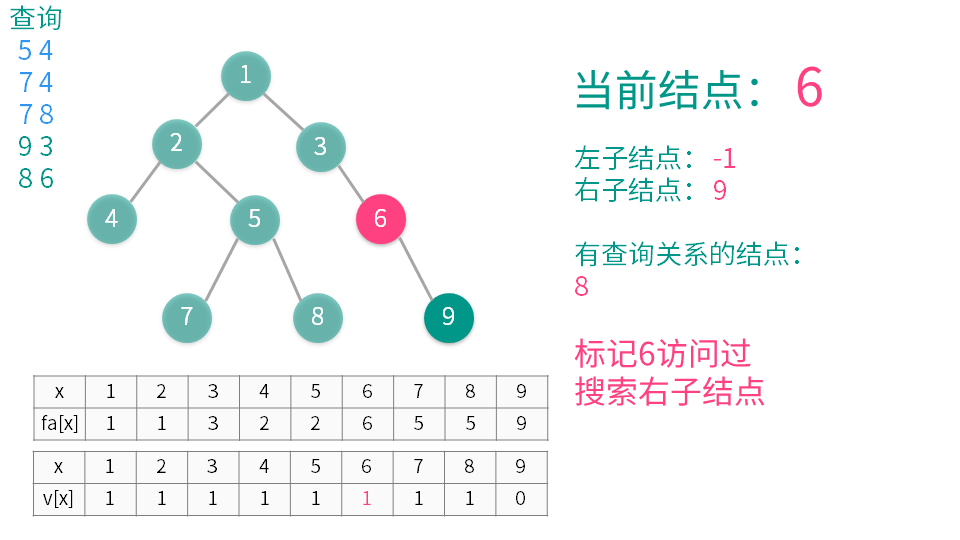
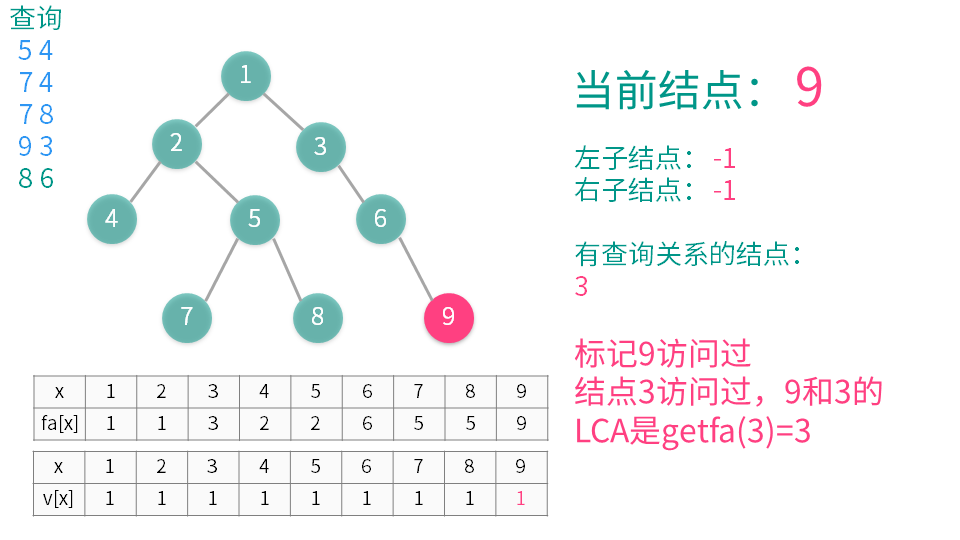
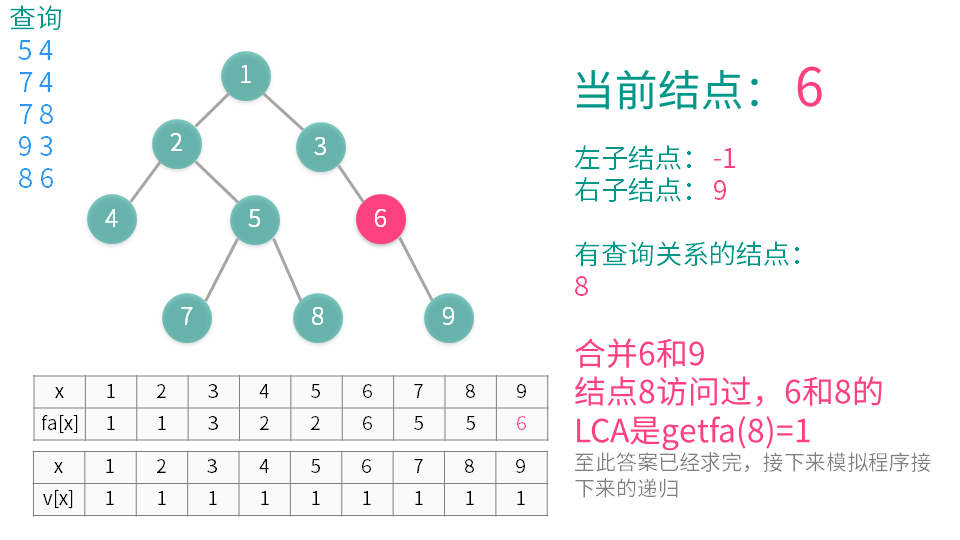
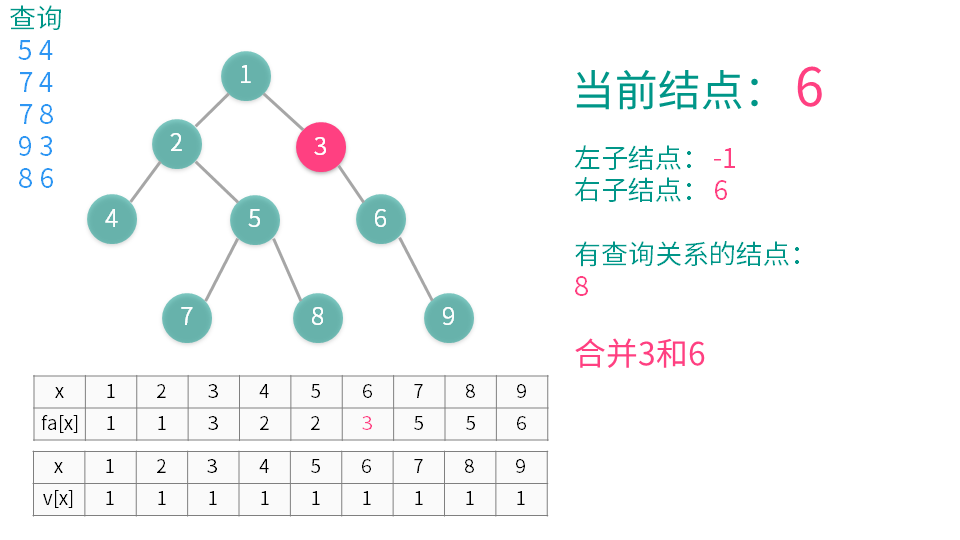
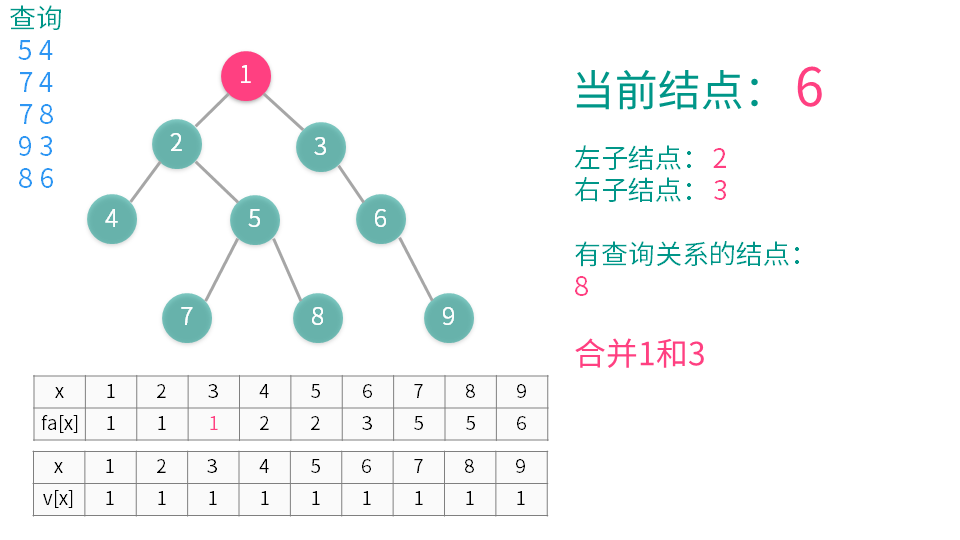
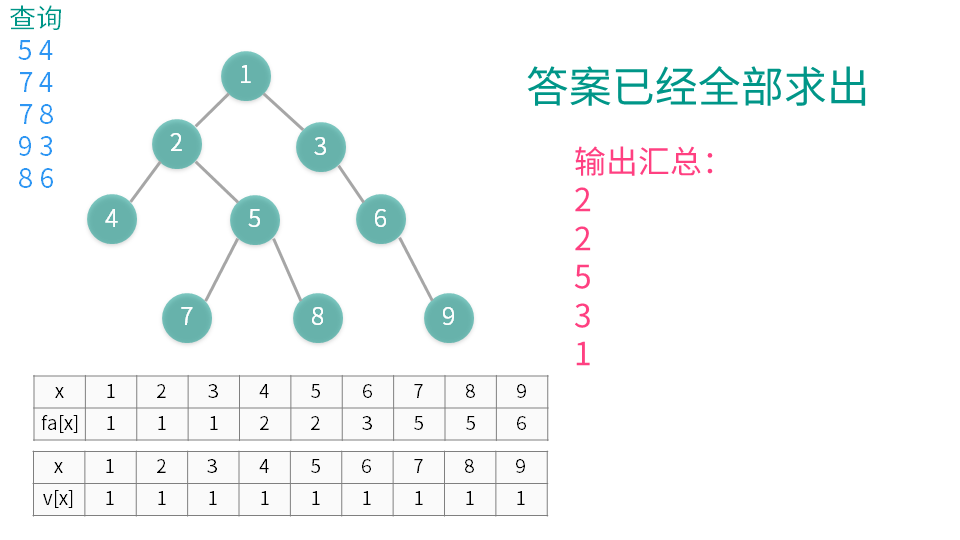





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· winform 绘制太阳,地球,月球 运作规律
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具
· AI 智能体引爆开源社区「GitHub 热点速览」