树链剖分算法解析
本文部分内容参考自 这篇博客 (写的很好 Orz ,建议大家也去看一下)
树链剖分是什么?用来做什么?
有一棵树,求解以下问题:
1将从 x 到 y 的路径上的每个结点权值增加 z
2求从 x 到 y 的路径上的每个结点的权值和/权值最大值/权值最小值
对于问题 1,我们可以用树上差分来求解。
对于问题 2,我们可以用类似前缀和的方法,预处理出每个点及其上面的点的权值和,利用 LCA ,减一减就得到了答案。
单独求解每个问题都很简单,这两种问题结合起来,上面的方法就不理想了。
而树链剖分可以巧妙地解决这一类问题。
一种对树链剖分直白的解释
树链剖分其实是把树的结点编号重组了,原先的每个结点都被分配了一个新的编号。
重新编号有什么好处?重新编号后的树,存在有若干条特殊的链,每条链上的新编号都是连续的。
这就方便了我们使用线段树/树状数组等数据结构来快速对这些链上的结点进行求和/求极值/修改。
注意:原树的每一个结点都被放入线段树中了,只是有一些树上的链对应线段树里的一些连续区间。
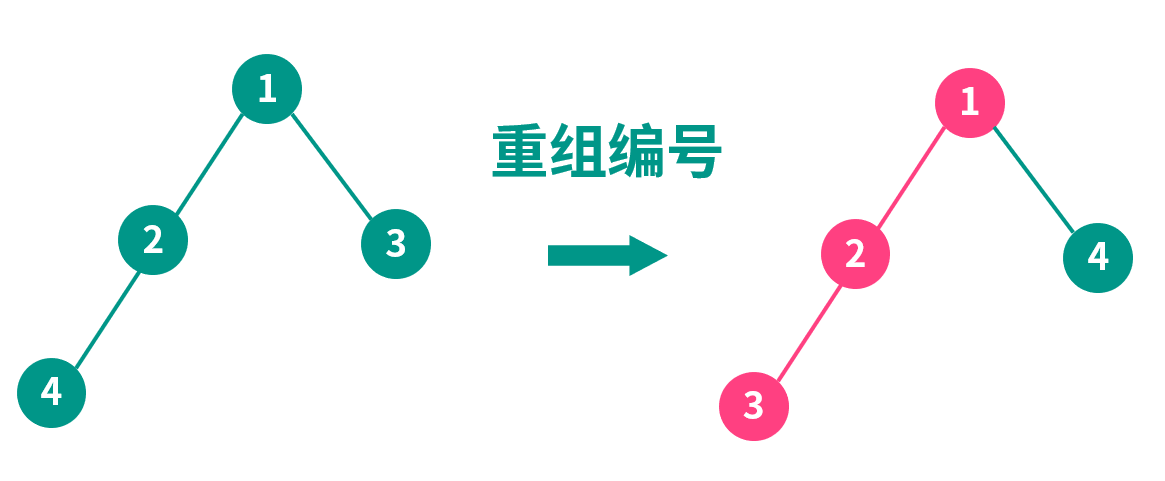
如图,重组编号后,使用这些编号为下标建立一棵线段树,那么 1-2-3 这条链的极值/和就可以很快求出了。
一些基本的概念
首先我们应该知道
在上文中我们已经了解,经过这种重组以后的树存在一些新编号连续的链,它们就叫做重链,而重链中的每一条边就叫做重边。
与之相对,其余的边就叫做轻边,它们组成的链就叫轻链。
你只需要记住重链是一些特殊的链即可。
那么如何划分重链呢?很简单。
对于一个结点,它的儿子分为轻儿子和重儿子。重儿子只有一个,其余的都是轻儿子。
如果一个子结点下面的结点很多(只要是子树中的都算),它的兄弟都比不上它,那它就是重儿子了。其余的都是轻儿子。
(如果每个儿子子树结点个数一样怎么办?当然是随便选一个)
(如果只有一个儿子怎么办?没有人竞争了,当然就是重儿子了)
例如下面这张图,结点 2 有 5 个子树结点,而结点 3 只有 3 个子树结点,结点 2 完胜,所以结点 2 就是结点 1 的重儿子。
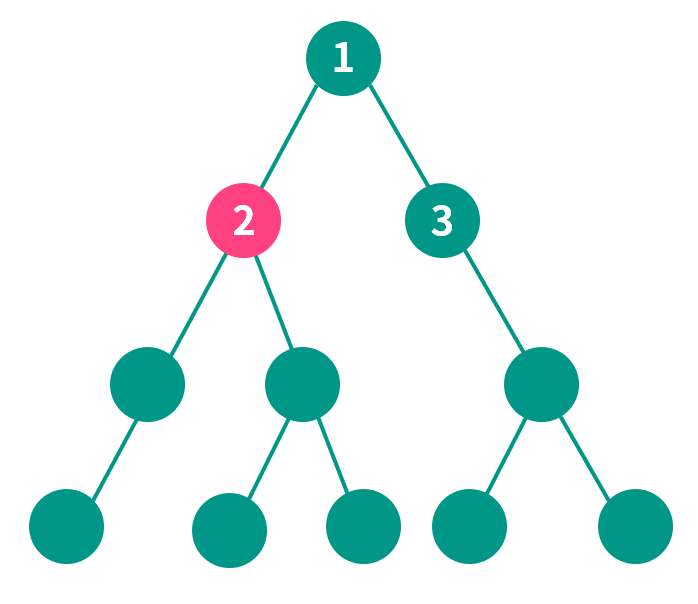
注意:树根是重儿子(虽然它没有父亲,就叫它重节点吧)
前面提到的重链同时也是重儿子组成的链,轻链当然就是轻儿子组成的链了。
小结一下
| 名字(概念) | 解释 |
| 重儿子/重结点 | 一个子树结点数量比它的每一个兄弟都多的结点,当然树根也是 |
| 轻儿子/轻结点 | 其余的结点(一个父结点除了重儿子以外的儿子) |
| 重链 | 重结点/重儿子组成的链 |
| 轻链 | 轻结点/轻儿子组成的链 |
| 重边 | 重链里的边 |
| 轻边 | 轻链里的边 |
和下文相关的一道例题
在开始讲代码之前,先看一道例题,下文围绕它展开。
下文代码的读入输出规范、数据范围等以这道例题为准。
预处理
预处理分为两次,不过很简单
第一次预处理
我们需要知道一个结点之下有几个子树结点,于是我们使用 size[i] 来表示结点 i 有几个子树节点。
我们需要知道结点的深度(后面有用),所以我们使用 d[i] 来表示结点 i 的深度(树根深度为 1)。
我们还需要知道每个结点的父亲结点(还是后面有用),所以我们使用 f[i] 来表示结点 i 的父亲结点。
我们必须要知道每个结点的重儿子,所以我们使用 son[i] 来表示结点 i 的重儿子。
我们当然可以用一遍 dfs 就预处理求出这几个数组。
void dfs1(int x,int fa,int deep){//当前结点 , 父亲结点 , 当前结点深度
f[x]=fa;//初始化 f[x] 为 x 的父亲结点
d[x]=deep;//初始化 d[x] 为 x 的深度
size[x]=1;//当前这个结点在子树中算一个结点,接下来没几行代码你就可以看到用递归去继续统计它了
for (int i=last[x];i;i=nextt[i]){//前向星枚举与当前结点有关系的结点
int t=to[i];//与当前结点有关系的结点
if (t==fa){//如果枚举到父亲结点了就跳过,既然递归到当前结点了,父亲结点肯定处理过了
continue;
}
dfs1(t,x,deep+1);//递归 (子结点,子结点的父亲为当前结点,深度+1)
size[x]+=size[t];//当子结点递归好以后,子结点的 size 肯定更新了,这个时候累计起来
if (size[t]>size[son[x]]){//如果当前这个子结点的子树结点数大于在这个结点之前枚举过的所有兄弟结点,那么更新重儿子为它
son[x]=t;
}
}
}
然后我们这么调用它: dfs1(root,root,1)
对调用的解释:从根节点开始 dfs,根节点的父节点是其本身,深度为1 (在本题中,根节点为编号为 1 的结点 ,所以本题中 root 为 1)
第二次预处理
等等,好像还少点什么。
光有这个没用啊,我们不是要重组编号吗。
我们需要知道一条重链的顶端结点编号,那么就用 top[i] 表示结点 i 所在重链的顶端结点编号。(如果它在轻链上,那就自成一链,顶端是它本身)
要知道顶端编号怎么办?我们肯定要 dfs ,dfs 肯定以重链为标准,那就顺便记录一下当前结点的 dfs 序,用 id[i] 来表示,这同时也是当前这个结点重新分配编号后的新编号。
既然都有新编号了,我们就干脆把结点按照新编号排成一个新数组,用 rk[i] 表示重排后的第 i 个点在重排前的编号。(不好理解?没关系,看代码就明白了)
这次的 dfs 和第一次有一些不一样,传的两个参数分别是 当前结点的编号 和 当前结点所在重链顶端结点的编号。
dfs 之前,需要知道:一个结点如果是重儿子,那么它是一条重链中的一员;如果是轻儿子,那么它是一条重链的顶端。
void dfs2(int x,int nowtop){//当前结点编号,当前结点所在重链顶端结点编号
top[x]=nowtop;//更新 top[x] 为结点 x 所在重链顶端结点编号
id[x]=++id[0];//更新结点 x 的 dfs 序(新编号),id[0] 类似于 top,记录当前已遍历了几个结点
rk[id[0]]=x;//把结点 x 放入 rk 数组末尾
if (!son[x]){//如果没有重儿子(也就是没有儿子,因为如果有一个儿子那必然是重儿子)
return;//那么直接回溯
}
dfs2(son[x],nowtop);//继续 dfs x 的重儿子,因为在同一条重链上,所以 nowtop 不变
for (int i=last[x];i;i=nextt[i]){//前向星枚举与当前结点有关系的结点
int t=to[i];//与之有关系的结点
if (t==son[x]||t==f[x]){//如果是重儿子或父亲就跳过这个点
continue;
}
dfs2(t,t);//因为轻儿子一定是重链顶端,所以也要 dfs,且顶端是其本身
}
}
我们这么调用它: dfs2(root,root)
本文使用的线段树模板
下面说明一下本文使用的线段树模板操作,以免混淆
build() 初始化线段树
updata(l,r,root,x,ans) 更新单点,将 x 点的值设为 ans
find_sum(maxl,maxr,root,l,r) 返回区间 [l,r] 中的总和
find_max(maxl,maxr,root,l,r) 返回区间 [l,r] 中的最大值
最后最后的预处理
我们得到了 rk 数组,现在只要开一棵线段树,build一下就好了。
//这里开两棵线段树,因为上面的题目需要求 max 和 sum
int tree[4*MAXN],tree2[4*MAXN];//tree 和 tree2 分别是存总和,最小值的线段树
void build(int l,int r,int root){
if (l==r){
tree[root]=s[rk[l]];//s 数组为旧编号每个点的权值,建树当然要用权值来赋值,rk[l] 为新编号第 l 个点对应的旧编号
tree2[root]=s[rk[l]];
return;
}
int mid=(l+r)/2;
build(l,mid,root*2);
build(mid+1,r,root*2+1);
tree[root]=tree[root*2]+tree[root*2+1];//分别用加和max更新两棵树
tree2[root]=max(tree2[root*2],tree2[root*2+1]);
}
↑ 你应该会的代码(线段树模板还有一部分就省略了)
那求上面那些其他的数组没用了?当然有。
下面我们进入正题。
树链剖分的操作
LCA
用树链剖分求 LCA 速度很快,也很简洁。
步骤
现在我们想求结点 x 和 y 的 LCA。
1判断 top[x] 是否等于 top[y]
2如果不等于,如果 d[x]>d[y],那么 x=f[top[x]] ,否则 y=f[top[y]] (更新深的结点)
3如果 top[x] 还是不等于 top[y],跳回第一步
4返回深度浅的结点的坐标(即 return d[x]>d[y]?y:x)
代码
int LCA(int x,int y){
while (top[x]!=top[y]){
if (d[top[x]]>d[top[y]]){
x=f[top[x]];
}else{
y=f[top[y]];
}
}
return d[x]>d[y]?y:x;
}
两点之间求和/极值
做法
我们基于 LCA 的代码,修改一些地方,加入统计即可
求最大值
int query_max(int x,int y){
int ans=-2147483647;
while (top[x]!=top[y]){
if (d[top[x]]>d[top[y]]){
ans=max(ans,find_max(1,n,1,id[top[x]],id[x]));//如果 x 往上跳了,就更新跳的这一段的最大值
x=f[top[x]];
}else{
ans=max(ans,find_max(1,n,1,id[top[y]],id[y]));//如果 y 往上跳了,就更新跳的这一段的最大值
y=f[top[y]];
}
}
if (x==y){//如果两点相遇,那么它们都在 LCA 结点上
ans=max(ans,s[x]);//更新 x 和 y 的 LCA 结点最大值
return ans;
}
if (d[x]<d[y]){
ans=max(ans,find_max(1,n,1,id[son[x]],id[y]));//更新较低那一点到 LCA 这一段的最大值
ans=max(ans,s[x]);//更新 LCA 最大值
}else{
ans=max(ans,find_max(1,n,1,id[son[y]],id[x]));//更新较低那一点到 LCA 这一段的最大值
ans=max(ans,s[y]);//更新 LCA 最大值
}
return ans;
}
求最小值
同上,只是把 max 改成 min,注意线段树也要修改
求和
同上,只是改成累加
int query_sum(int x,int y){
int ans=0;
while (top[x]!=top[y]){
if (d[top[x]]>d[top[y]]){
ans+=find_sum(1,n,1,id[top[x]],id[x]);
x=f[top[x]];
}else{
ans+=find_sum(1,n,1,id[top[y]],id[y]);
y=f[top[y]];
}
}
if (x==y){
ans+=s[x];
return ans;
}
if (d[x]<d[y]){
ans+=find_sum(1,n,1,id[son[x]],id[y]);
ans+=s[x];
}else{
ans+=find_sum(1,n,1,id[son[y]],id[x]);
ans+=s[y];
}
return ans;
}
单点修改
很简单,直接上代码
void change(int x,int y){
s[x]=y;
updata(1,n,1,id[x],y);//线段树单点修改
}
两点之间权值修改
需要支持区间修改的线段树,只要把之前求 max 代码的更新过程改成修改过程就好了。
这里的代码是 洛谷 P3384 的 AC 代码,标准也和这道题一样
#include<bits/stdc++.h>
#define MAXN 200005
using namespace std;
long long last[MAXN*2],to[MAXN*2],nextt[MAXN*2],topp=0;
long long s[MAXN],f[MAXN],d[MAXN],size[MAXN],son[MAXN],rk[MAXN],top[MAXN],id[MAXN];
long long sum[MAXN*4],min[MAXN*4],max[MAXN*4],tag[MAXN*4];
long long n,q;
void pushup(long long rt){
sum[rt]=sum[rt*2]+sum[rt*2+1];
}
void build(long long l,long long r,long long rt){
if(l==r){
sum[rt]=s[rk[l]];
return;
}
long long m=(l+r)/2;
build(l,m,rt*2);
build(m+1,r,rt*2+1);
pushup(rt);
}
void pushdown(long long rt,long long ln,long long rn){
if(tag[rt]){
sum[rt*2]+=ln*tag[rt];
sum[rt*2+1]+=rn*tag[rt];
tag[rt*2]+=tag[rt];
tag[rt*2+1]+=tag[rt];
tag[rt]=0;
}
}
void update(long long L,long long R,long long C,long long l,long long r,long long rt){
if(L<=l&&r<=R){
sum[rt]+=C*(r-l+1);
tag[rt]+=C;
return ;
}
long long m=(l+r)/2;
pushdown(rt,m-l+1,r-m);
if(L<=m){
update(L,R,C,l,m,rt*2);
}
if(R>m){
update(L,R,C,m+1,r,rt*2+1);
}
pushup(rt);
}
long long query(long long L,long long R,long long l,long long r,long long rt){
long long ans=0;
long long m=(l+r)/2;
if(L<=l&&R>=r){
return sum[rt];
}
pushdown(rt,m-l+1,r-m);
if(L<=m){
ans+=query(L,R,l,m,rt*2);
}
if(R>m){
ans+=query(L,R,m+1,r,rt*2+1);
}
return ans;
}
void add(long long a,long long b){
nextt[++topp]=last[a];
to[topp]=b;
last[a]=topp;
}
void dfs1(long long x,long long fa,long long deep){
f[x]=fa;
d[x]=deep;
size[x]=1;
for (long long i=last[x];i;i=nextt[i]){
long long t=to[i];
if (t==fa){
continue;
}
dfs1(t,x,deep+1);
size[x]+=size[t];
if (size[t]>size[son[x]]){
son[x]=t;
}
}
}
void dfs2(long long x,long long nowtop){
top[x]=nowtop;
id[x]=++id[0];
rk[id[0]]=x;
if (!son[x]){
return;
}
dfs2(son[x],nowtop);
for (long long i=last[x];i;i=nextt[i]){
long long t=to[i];
if (t==son[x]||t==f[x]){
continue;
}
dfs2(t,t);
}
}
long long LCA(long long x,long long y){
while (top[x]!=top[y]){
if (d[top[x]]>d[top[y]]){
x=f[top[x]];
}else{
y=f[top[y]];
}
}
return d[x]>d[y]?y:x;
}
long long query_sum(long long x,long long y){
long long ans=0;
while (top[x]!=top[y]){
if (d[top[x]]>d[top[y]]){
ans+=query(id[top[x]],id[x],1,n,1);
x=f[top[x]];
}else{
ans+=query(id[top[y]],id[y],1,n,1);
y=f[top[y]];
}
}
if (x==y){
ans+=query(id[x],id[x],1,n,1);
return ans;
}
if (d[x]<d[y]){
ans+=query(id[son[x]],id[y],1,n,1);
ans+=query(id[x],id[x],1,n,1);
}else{
ans+=query(id[son[y]],id[x],1,n,1);
ans+=query(id[y],id[y],1,n,1);
}
return ans;
}
void change(long long x,long long y,long long z){
while (top[x]!=top[y]){
if (d[top[x]]>d[top[y]]){
update(id[top[x]],id[x],z,1,n,1);
x=f[top[x]];
}else{
update(id[top[y]],id[y],z,1,n,1);
y=f[top[y]];
}
}
if (x==y){
update(id[x],id[x],z,1,n,1);
return;
}
if (d[x]<d[y]){
update(id[son[x]],id[y],z,1,n,1);
update(id[x],id[x],z,1,n,1);
}else{
update(id[son[y]],id[x],z,1,n,1);
update(id[y],id[y],z,1,n,1);
}
}
long long root,mod;
int main(){
cin>>n>>q>>root>>mod;
for (long long i=1;i<=n;i++){
cin>>s[i];
}
for (long long i=1;i<=n-1;i++){
long long a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
dfs1(root,root,1);
dfs2(root,root);
build(1,n,1);
long long t,x,y,z;
while (q--){
cin>>t>>x;
if (t==1){
cin>>y>>z;
change(x,y,z);
}
if (t==2){
cin>>y;
cout<<query_sum(x,y)%mod<<endl;
}
if (t==3){
cin>>y;
update(id[x],id[x]+size[x]-1,y,1,n,1);
}
if (t==4){
cout<<query(id[x],id[x]+size[x]-1,1,n,1)%mod<<endl;
}
}
}
模板题代码
就是上文的那道题
#include<bits/stdc++.h>
#define MAXN 100000
using namespace std;
int last[MAXN],to[MAXN],nextt[MAXN],topp=0;
int s[MAXN],f[MAXN],d[MAXN],size[MAXN],son[MAXN],rk[MAXN],top[MAXN],id[MAXN];
int tree[4*MAXN],tree2[4*MAXN];
int n,q;
void build(int l,int r,int root){
if (l==r){
tree[root]=s[rk[l]];
tree2[root]=s[rk[l]];
return;
}
int mid=(l+r)/2;
build(l,mid,root*2);
build(mid+1,r,root*2+1);
tree[root]=tree[root*2]+tree[root*2+1];
tree2[root]=max(tree2[root*2],tree2[root*2+1]);
}
void updata(int l,int r,int root,int x,int ans){
if(r<x||l>x){
return;
}
if(l==r&&l==x){
tree[root]=ans;
tree2[root]=ans;
return;
}
int mid=(l+r)/2;
updata(l,mid,root*2,x,ans);
updata(mid+1,r,root*2+1,x,ans);
tree[root]=tree[root*2]+tree[root*2+1];
tree2[root]=max(tree2[root*2],tree2[root*2+1]);
}
long long find_sum(int maxl,int maxr,int root,int l,int r){
if (maxl>r||maxr<l){
return 0;
}
if (l<=maxl&&maxr<=r){
return tree[root];
}
int mid=(maxl+maxr)/2;
return find_sum(maxl,mid,root*2,l,r)+find_sum(mid+1,maxr,root*2+1,l,r);
}
int find_max(int maxl,int maxr,int root,int l,int r){
if (maxl>r||maxr<l){
return -2147483647;
}
if (l<=maxl&&maxr<=r){
return tree2[root];
}
int mid=(maxl+maxr)/2;
return max(find_max(maxl,mid,root*2,l,r),find_max(mid+1,maxr,root*2+1,l,r));
}
void add(int a,int b){
nextt[++topp]=last[a];
to[topp]=b;
last[a]=topp;
}
void dfs1(int x,int fa,int deep){
f[x]=fa;
d[x]=deep;
size[x]=1;
for (int i=last[x];i;i=nextt[i]){
int t=to[i];
if (t==fa){
continue;
}
dfs1(t,x,deep+1);
size[x]+=size[t];
if (size[t]>size[son[x]]){
son[x]=t;
}
}
}
void dfs2(int x,int nowtop){
top[x]=nowtop;
id[x]=++id[0];
rk[id[0]]=x;
if (!son[x]){
return;
}
dfs2(son[x],nowtop);
for (int i=last[x];i;i=nextt[i]){
int t=to[i];
if (t==son[x]||t==f[x]){
continue;
}
dfs2(t,t);
}
}
int LCA(int x,int y){
while (top[x]!=top[y]){
if (d[top[x]]>d[top[y]]){
x=f[top[x]];
}else{
y=f[top[y]];
}
}
return d[x]>d[y]?y:x;
}
void change(int x,int y){
s[x]=y;
updata(1,n,1,id[x],y);
}
int query_max(int x,int y){
int ans=-2147483647;
while (top[x]!=top[y]){
if (d[top[x]]>d[top[y]]){
ans=max(ans,find_max(1,n,1,id[top[x]],id[x]));
x=f[top[x]];
}else{
ans=max(ans,find_max(1,n,1,id[top[y]],id[y]));
y=f[top[y]];
}
}
if (x==y){
ans=max(ans,s[x]);
return ans;
}
if (d[x]<d[y]){
ans=max(ans,find_max(1,n,1,id[son[x]],id[y]));
ans=max(ans,s[x]);
}else{
ans=max(ans,find_max(1,n,1,id[son[y]],id[x]));
ans=max(ans,s[y]);
}
return ans;
}
int query_sum(int x,int y){
int ans=0;
while (top[x]!=top[y]){
if (d[top[x]]>d[top[y]]){
ans+=find_sum(1,n,1,id[top[x]],id[x]);
x=f[top[x]];
}else{
ans+=find_sum(1,n,1,id[top[y]],id[y]);
y=f[top[y]];
}
}
if (x==y){
ans+=s[x];
return ans;
}
if (d[x]<d[y]){
ans+=find_sum(1,n,1,id[son[x]],id[y]);
ans+=s[x];
}else{
ans+=find_sum(1,n,1,id[son[y]],id[x]);
ans+=s[y];
}
return ans;
}
int main(){
cin>>n;
for (int i=1;i<=n-1;i++){
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
dfs1(1,1,1);
dfs2(1,1);
for (int i=1;i<=n;i++){
cin>>s[i];
}
build(1,n,1);
cin>>q;
string S;
int x,y;
while (q--){
cin>>S>>x>>y;
if (S=="QMAX"){
cout<<query_max(x,y)<<endl;
}else if (S=="QSUM"){
cout<<query_sum(x,y)<<endl;
}else{
change(x,y);
}
}
}


