欧拉回路，一笔画问题

本来打算写证明的，果然还是太菜orz

欧拉回路就是给一个图，存在一条回路把所边经过且每条边只经过一次。

对于无向图：

　　存在欧拉回路的条件：每个点的度都为偶数；

　　存在欧拉路的条件：有且只有两个点的度为一，且这两个点分别为起点和终点；

对于有向图：

　　存在欧拉回路的条件：每个点出度等于入度；

　　存在欧拉路的条件：存在一个点出度比入度多一作为起点，存在一点入度比出度多一作为终点，其余点出度等于入度；

求欧拉回路的方法——基本（套圆）法

　　dfs搜索，不能再往下走便回溯，回溯时记录路径，回溯时不清除对边的标记，最后求出来的路径就是欧拉回路。

 

 

 

 

 

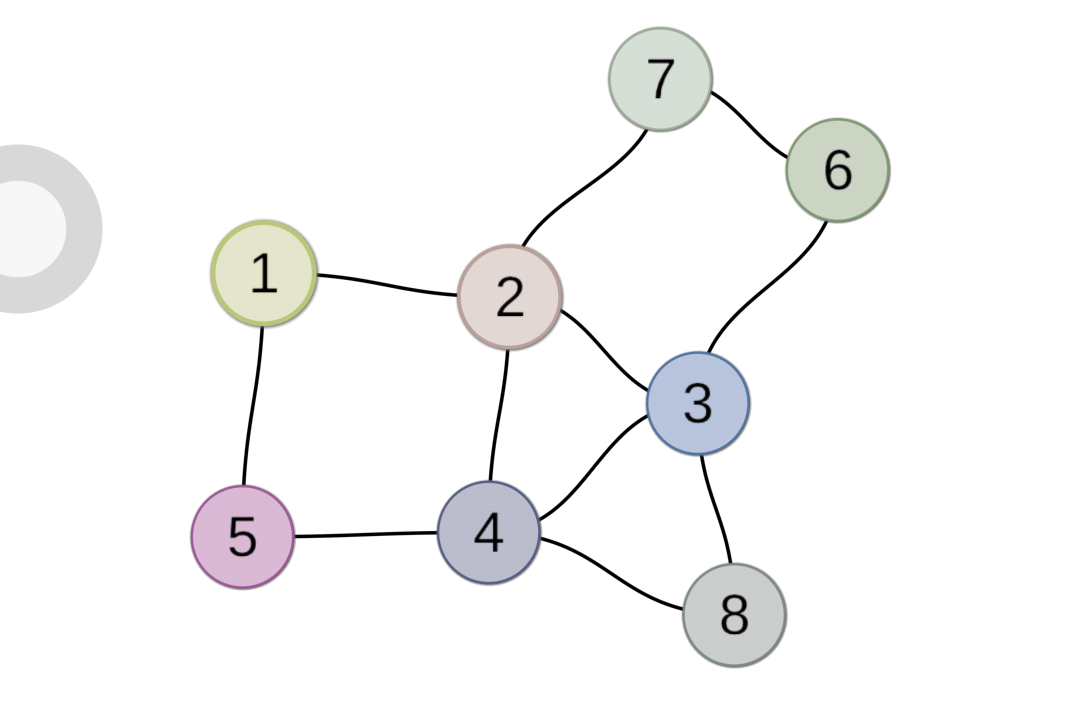
（1）走<1,2>,<2,3>,<3,4>,<4,5>,<5,1>,然后无路可走，就回溯记录下回溯路径<1,5>,<5,4>,4点有其它路壳走。

（2）<4,8>,<8,3>,<3,6>,<6,7>,<7,2>，<2,4>,无路可走，然后回溯<1,5>,<5,4>,<4,2>,<2,7>,<7,6>,<6,3>,<3,8>,<8,4>,<4,3>,<3,2>,<2,1>。

记录下的路径<1,5>,<5,4>,<4,2>,<2,7>,<7,6>,<6,3>,<3,8>,<8,4>,<4,3>,<3,2>,<2,1>便是一条欧拉回路。

#include <iostream>
#include <vector>
using namespace std;
vector <int > aa[155];
int bb[155][155],ee[155];
vector <int > cc;
int dd[11][2]={
{1,2},{1,5},{2,4},{2,3},{2,7},{4,5},{4,8},{4,3},{8,3},{3,6},{6,7}};
void bfs (int t)
{
    for (vector <int > ::iterator i=aa[t].begin();i!=aa[t].end();i++)
    {
        if (!bb[*i][t]) continue;
        bb[*i][t]=0;
        bb[t][*i]=0;
        bfs (*i);
    }
    cc.push_back(t);
}
int main ()
{
    int n=8,m=11;
    for (int i=0;i<n;i++)
    {
        aa[i].clear();
        ee[i]=0;
    }
    for (int i=0;i<m;i++)
    {
        aa[dd[i][0]].push_back(dd[i][1]);
        aa[dd[i][1]].push_back(dd[i][0]);
        bb[dd[i][1]][dd[i][0]]=1;
        bb[dd[i][0]][dd[i][1]]=1;
    }
    bfs(1);
    for (vector <int >::iterator i=cc.begin();i!=cc.end();i++)
        cout <<*i<<" ";
    cout <<endl;
}

运行结果：

。。。。。。。。