SAS学习笔记26 方差分析
对于多于两组(k>2)样本均数的比较,t检验不再适用,方差分析(analysis of variance, ANOVA)则是解决上述问题的重要分析方法。方差分析由R.A.Fisher(1923)首先提出,故又称为F检验,其基本思想是将全部观测值的总变异按影响因素分解为相应的若干部分变异,在此基础上,计算假设检验的统计量F值,实现对总体均数是否有差别的推断。
完全随机设计的方差分析
随机区组设计的方差分析
多个样本均数的两两比较
根据方差分析的结果,若拒绝H0接受H1,则可以推断K组均数不全相同,然而,究竟哪些组不同,需要进一步对多个样本均数进行两两比较或称多重比较(multiple comparison)。对此若用t检验对K组均数进行两两比较,共需比较
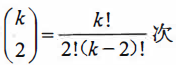
如k=5,若规定检验水准α=0.05,在原假设H0成立的条件下,10次检验均不犯l类错误的概率为0.9510=0.5987,累积犯I类错误的概率为1-0.5987 = 0.4013,明显大于0.05。因此,均数间的多重比较不能直接使用两均数比较的t检验。
多重比较的方法有很多,如Dunnett-t检验、LSD-t检验、SNK-q(Student-Newman-Keuls)法、Tukey法、Scheffe法、Sidak t检验和Bonferroni t检验等。

比较常用的是SNK法,SNK法的检验统计量为q,故又称为q检验

方差齐性检验
多组数据的方差齐性检验,应用较多的是Bartlett检验法和Levene检验法。Bartlett检验法主要适用于正态分布资料的方差齐性检验问题,如资料不服从正态分布,则可采用Levene检验法。
其他设计类型的方差分析
析因设计(factorial design)是一种多因素多水平交叉组合的实验设计方法。在医学研究中,如果涉及两个或多个处理因素,而研究者希望了解各处理因素的效应以及因素间的交互作用时,则可以采用析因设计方法。
重复测量设计(repeated measurement design)指同一受试对象的某一观察指标在不同时间点上进行多次测量的设计方法,如服用某种药物后测定不同时间点的血药浓度,接受治疗后在不同时间点上对某指标进行测量,这种设计方法在医学研究领域中有着广泛的应用,常用来分析不同处理在不同时间点上的变化情况。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号