SciTech-EECS-Control System-PID(Proportional,Integral,Derivative): 控制系统 的 PID控制算法: 比例:瞬态Error(快速逼近)+积分:稳态Error(稳定终值)+微分:平滑(减少逼近时震荡) 的 控制算法

参考文献

本文介绍PID控制算法的工作原理，通过“水塔加水”的例子阐述 P比例、I积分 和 D微分 三部分的作用。

  • P(Proportion,比例): 控制解决 当前误差作出反应，
  • I(Integration,积分): 控制解决 过去累积的误差，
  • D(Differentiation,微分): 预测未来的误差, 平滑系统响应。

PID最优参数的确定，才是重点，通常需要通过实验和调整。

PID(比例-积分-微分)控制是业内最常用的控制算法，在工业控制领域有很高的接受度。
PID控制器的广泛应用得益于其在多种操作条件下稳定的性能，以及易操作的特性。
工程师可以用简单直观的方式实现PID控制。

PID控制有三个基本要件：比例(proportional)、积分(integral)、微分(derivative)。
通过这三种不同的计算方法可获取最优化结果。

本文主要介绍主题:

  • 闭环系统、
  • PID经典理论、
  • 调整闭环控制系统的效果

LabVIEW的PID工具包和PID VI的易用性也在本文的讨论范围。


PID控制系统

PID控制器 可接收来自 传感器的输入数据、计算实际值 与 设定值 之间的差值，
并根据温度、流速、速度、压力和电压等控制变量调整输出。
该仪器通过三种机制实现这一点：

  • 比例控制，对当前误差作出反应；
  • 积分控制，解决过去累积的误差；
  • 微分控制，预测未来的误差。

PID控制器将这三个值相加来计算输出。
通过这种架构，PID控制器能够有效维持过程控制和系统稳定性。
开始定义PID控制器的参数之前，要先了解闭环系统及其相关术语。



闭环系统

PID控制 在 闭环系统 或 PID循环 运行，这是一种读取传感器以提供恒定反馈的控制机制，以固定间隔(称为固定循环速率)计算所需的 激励器输出。

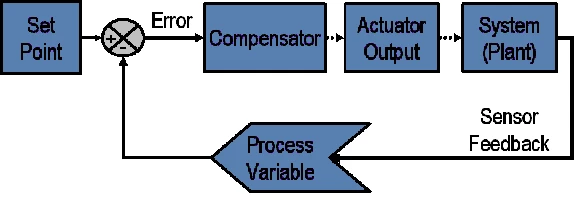
  • 在一个典型的PID控制系统，
  • 过程变量 是 需要被控制的 系统变量。例如，温度(ºC)、压强(psi)、流速（升/分钟）。
    传感器用于测量过程变量，并对控制系统做出反馈。
  • 设定值 是 过程变量的期望值 或 必须达到的值。
    例如，在一个温控系统，设定温度值为100摄氏度。
  • 补偿器(控制系统算法), 任意时间点，使用 过程变量 和 设定值 的差值, 得到期望的 激励器输出驱动系统(设备)。
    例如，测量得温度(过程变量)为100 ºC, 期望的温度设定值为120 ºC, 控制器算法的激励器输出将指示打开加热器。
    驱动激励器打开加热器，整个系统就逐渐变热，温度过程变量测得的结果也会增加。
  • 不响应期: 改变过程变量 和 观测到该改变 之间的时间延迟
  • 循环周期: 调用控制算法之间的时间Interval(间隔)是循环周期时间。是闭环系统的重要参数.
    变化迅速或操作复杂的系统，需要更短的周期(更快的循环速率)。
  • 干扰抑制: 控制系统的克服干扰的能力。
    • 干扰:
      在很多情况下，激励器输出 并不是对系统有影响的唯一信号。
      例如，在温度舱内，可能会有冷空气源。 冷空气吹入舱内时，会扰动环境温度。这类扰动因素叫做干扰。
    • 系统一般都有一个或多个影响 "过程变量" 或 "过程变量测量值" 的 "干扰"
      我们在设计控制系统时，通常会尽可能减少对过程变量的干扰因素。
  • 稳定性: 控制系统 对 干扰和非线性 的耐受度。
  • PID循环如图1所示。

术语定义

控制设计 过程 从定义性能需求开始。
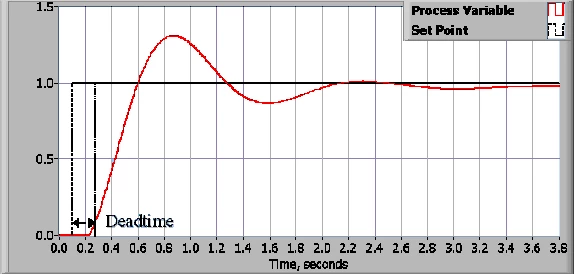
控制系统的性能 常通过应用一个“阶跃函数”作为“设定值(命令变量)”，然后测量“过程变量”的响应。
一般，我们通过测量“定义的波形特征”来“量化响应”。

  • 上升时间: 系统从"稳定状态(或最终值)"的 10% 上升到 90% 的"所需时间"。
  • 过冲百分比: "过程变量" 超过 "最终值"的"百分比数"，并用"最终值的百分比"表示。
  • 稳定时间: "过程变量值" 稳定在 "最终值(通常是5%)范围内的"所需时间"。
  • 稳定状态误差: "过程变量" 和 "设定值" 之间的"最终差值"。
  • 请注意，这些值的确切定义在学术和工业上的定义不尽相同。


定义"最坏情况:":

  • 使用这些量来定义控制系统的性能要求时，有必要定义控制系统满足这些设计需求时可能遇到的“最坏情况”。
  • 干扰方面:
    系统一般都有一个 "干扰"(影响 "过程变量" 或 "过程变量测量值" )。
    所以，要设计一个在最坏情况下都能圆满工作的控制系统。
  • 耐受度方面: 控制系统对干扰和非线性的耐受度，被称为控制系统的稳定性。
    在某些情况下，对于一个 给定控制输出 的 系统反馈 可能会因 时间或某个有关变量 而变化。
    在非线性系统，控制参数 在 某个时刻 给出的 期望响应，但是在另一个时刻可能无法给出满意的响应。
    例如，舱室几乎为空时，其对 "加热器输出的响应" 比 舱室填满或几乎填满液体时 更快。
  • 不响应期方面: 不响应期是过程变量改变和观测到该改变之间的时间延迟。
    有些系统会出现非预期的不响应期。不响应期也可能是因为系统或输出激励器响应控制命令比较缓慢。
    如:
    温度传感器离水阀较远, 无论水阀打开或关闭，传感器都无法立即监测到温度变化. 阀门开关速度慢。
    在化工厂，造成不响应期的常见原因是化学试剂在管道流通需要的时间。
  • 循环周期 方面:
    变化迅速或操作复杂的系统，需要更快的循环速率。

一旦指定性能需求，即可开始 检查系统 并 选择合适的控制方案。
在大多数应用程序，PID控制程序必须提供结果。


PID理论

  • Proportional比例响应

    • 比例模块仅仅取决于设定值和过程变量之间的差值。这个差值被称为“Error(误差)”.
    • Kc(比例增益)决定"输出响应"对"误差信号"的"比例"。
      例如, 如错误项的幅值为10，比例增益为5, 则将产生比例响应为50。
      • 增加Kc(比例增益), 一般都将提高控制系统响应的速度。
      • 过大Kc(比例增益), 过程变量会出现振荡。
      • 超大Kc(比例增益), 系统振荡会越来越大, 使得系统变得不稳定, 甚至失控。

  • Integral积分响应
    积分模块 sum(累加)一段时间内的误差。

    • 即使是"很小误差"也会使"积分响应"缓慢增加。
    • 积分响应: 目的是将"稳定状态的误差"稳0: 积分响应根据时间持续增加, 除非0误差.
    • 积分饱和: 当"积分操作"满足"控制器的条件", 而"控制器"还 "未将误差保持在0" 时的一种现象.
    • 稳定状态误差: 是过程变量和设定值之间的差值.

  • Differential微分响应
    如果过程变量快速增加，微分分量会导致输出减少。
    微分响应: 与过程变量的变化率(注意是"变化率"而"不是变化量")之间成比例关系。
    微分响应对"过程变量的噪声"特别敏感

    • 增加Td(微分时间), 会使控制系统对 "误差的反应" 更加剧烈，也会增加整个控制系统的响应时间。
    • 小Td(微分时间): 大多数实用控制系统使用非常小的Td(微分时间),
      如 传感器反馈信号有噪声 或 控制循环速率太低，微分响应会使控制系统变得不稳定。

调整

设置P、I、D最佳增益，从而得到控制系统理想反馈的过程叫做整定。
PID整定方法有很多种。本文主要介绍"试错法"和"Ziegler Nichols法"。

试错法
我们可通过试错法获得PID控制器的增益。
当工程师了解了每个增益参数的有效性后，该方法就变得相对简单。
在该方法，

  • 先将I、D设置为0只调整P**,
  • P的比例增益增加到循环输出开始振荡为止。
    增加比例增益时，系统变得更快，但是要保证系统不会变得不稳定。
  • 一旦设置好P，要有“期望的"快速响应"”:
    积分项增加以停止振荡。调整积分项, 达到最小稳定状态误差。
    积分项会减少稳定状态的误差，但是会增加过冲。
    合理的过冲对于一个快速系统来说是必要的，这样才能立即响应变化。
  • 一旦设置好P、I，要不仅“有最小稳定状态误差”而且“灵敏而不过敏”:
    微分项一直增加, 直到循环对于设定值来说足够快。
    增加微分项会减少过冲，产生更高的稳定性增益，但系统会对噪声变得异常敏感。
  • 大多数情况下，工程师在设计时需要权衡控制系统的各种特性，以便更好地满足要求。

Ziegler-Nichols法
另一种常用的整定PID控制器的方法。
该方法与试错方法类似，即:
将I、D设置为0，且P增加到循环开始振荡为止。
一旦发生振荡，需观察关键增益Kc和振荡周期Pc。
然后根据下表所示调整P、I、D。

控制 P Ti Td
P 0.5Kc - -
PI 0.45Kc Pc/1.2 -
PID 0.60Kc 0.5Pc Pc/8

表1：Ziegler-Nichols整定，使用振荡法。




一文读懂PID控制算法

原理上真正理解PID控制,

  • PID控制是应用非常广泛的控制算法。
    小到控制一个元件的温度，大到控制无人机的飞行姿态和飞行速度等等，都可以使用PID控制。
  • 原理上来理解PID控制。
    理解原理才能知道为什么要用比例，微分，积分这3个项才能实现最好的控制。

PID(proportion, integration, differentiation)

其实就是指比例，积分，微分控制。先上图片和公式:

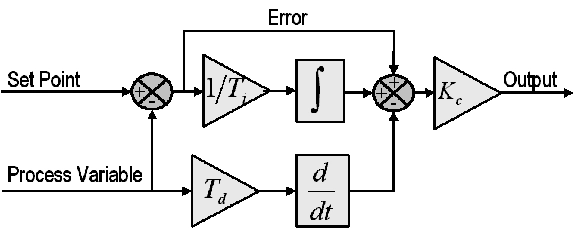
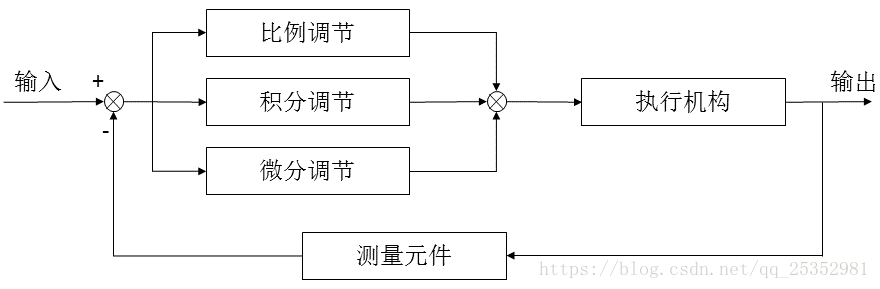
  • PID控制原理图:

  • PID控制公式:
    kp是一系数; 括号内: 第一项:"比例项", 第二项:"积分项", 第三项:"微分项":

    \[\large u(t)= K_{p} \times( error(t) + \dfrac{1}{T_{I}} \int error(t) dt + T_{D} \dfrac{d{error(t)}}{d{t}} ) \]

  • 离散化公式(), 则控制可以化为:
    实际离散场合是大多数, 适合编程实现. 系数都要实验确定:
    \(\large \begin{array}{rll} u(k) & = & K_{p} \ err(k) + K_{i} \overset{ k }{\underset{n=0}{\sum}} { err(n) } + K_{d} (\ err(k) - err(k-1)\ ) \\ & & K_{p} \text{: 系数, Proportion 项的} \\ & & K_{i} \text{: 系数, Integration 项的} \\ & & K_{d} \text{: 系数, Differentiation 项的} \\ & \Uparrow & \\ u(k) & = & K_{p} \ err(k) + K_{p} \dfrac{T}{T_{i}} \overset{ k }{\underset{n=0}{\sum}} { err(n) } + K_{p} \dfrac{ T_{d}}{T} (\ err(k) - err(k-1)\ ) \\ & \Uparrow & \\ u(k) & = & K_{p} \times(\ \ err(k) + \dfrac{T}{T_{i}} \overset{ k }{\underset{n=0}{\sum}} { err(n) } + \dfrac{T_{d}}{T} (\ err(k) - err(k-1)\ ) \ \ ) \\ \end{array}\)

  • 如何确定三个项的系数，要大量实验+经验+需求来决定。
    通过不断的尝试和正确思考，就能选取合适的系数，实现优秀的控制器。


PID控制算法原理

PID控制算法公式
用“系统输出”作为“PID控制的输入”后，
将 “系统输出” 经过 比例，积分，微分 3种运算方式，叠加到输入，从而控制系统的行为，

实例背景假设
假设, 有一个水塔，要通过“系统控制”满足一定的需求:

  • 初始时刻: "初始水位=0.2"， 是 0.2米
  • 最终目的: "目标水位=1.0"， 要保证永远的维持在1米的高度
  • 当前时刻: "当前水位=0.2"，初始化。
    "当前Error" = "目标水位" - "当前水位", 即 $\large error=0.8 $
  • "加水量u": 一人通过往水塔加水的方式来控制水位。

Proportion比例控制算法

如果只用 Proportion比例控制算法 是指“加水量u” 和 “误差error” 成正比。

\[\large u_i =kp \times error(t_i), \ kp \text{ 是 比率 }, \ error \text{ 是 (目标值-当前值) } \]

假设 \(\large kp=0.5, \ target_height=1.0\),

\[\large \begin{array}{llll} t_0 : & u_0 = 0, & curr_0=0.2, & error_0=0.8 \\ t_1 : & u_1 = 0.5 * 0.8 = 0.4, & curr_1 = 0.6, & error_1=0.4 \\ t_2 : & u_2 = 0.5 * 0.4 = 0.2, & curr_2=0.8, & error_2=0.2 \\ \cdots & & & \end{array} \]

  • 如此循环，就是 比例控制算法 的运行方法。最终水位会达到我们需要的1米。
  • $\large kp $取值可以变化，系统最后都会达到1米，不会有"稳态误差"。
    $\large kp $越小，越精准，响应越慢("调控次数"越多)。
    $\large kp $越大，响应快，可能振荡并且系统稳态可能达不到最终目标值。(在目标值上下振荡)。

Proportion比例控制 没法表示 “稳态误差”:

  • 什么是 "稳态误差" ? 以及 "为什么有稳态误差"。
    上例，根据$\large kp $取值不同，系统最后都会达到1米，不会有稳态误差。
    假设, $\large kp = 0.5 $, 但是, 每次加水过程都用0.1米高的水(加水同时用水)。
    那么, 可能 经过几次加水后，水位稳定不变 但是 稳定值 不等于 目标值.
    • 因为，水位为0.8时，则error=0.2. 每次加水量u=0.5*0.2=0.1.
    • 同时，每次加水0.1, 又用0.1, 加水量 和 用水量 抵消, 水位不变, 系统稳定.
    • 目标1米，系统稳定0.8米。“系统稳定状态时的误差”就是“稳态误差”。

实际这种类似 "生产 同时 消费"的情况, 往往更加常见，
比如控制汽车运动，摩擦阻力 就相当于是“用水”，
控制机械臂、无人机的飞行，各类阻力 和消耗 都可以理解为上例的“用水.
所以，只用比例控制，在很多时候并不能满足要求。


积分控制算法

还用上例，如果仅用Proportion比例，可能存在 稳态误差。
控制上在\(\large kp\)之外引入一个分量，该分量和Error(误差)的 积分 是 正比关系。
所以，比例+积分控制算法为：
$\large u= kp \times error + ki \times \int error error, \ ki \text{ 是 误差积分 的 比率 }, \ \text{ 离散情况的积分 其实用的"sum累加" } $

还用上例，
第一次的误差error是0.8，第二次的误差是0.4，
Error积分\(\large \int error= 0.8 + 0.4 = 1.2\)
这时控制量, 不仅要有 Proportion比例的, 还要有: \(\large ki \times \int error= ki(0.8 + 0.4) = 1.2ki\)。
Error积分项会将前面若干次的Error误差积分累计，所以能很好的消除稳态误差.
假设: 在仅有Proportion比例项的情况，系统存在稳态误差，如上例的0.8，
新增积分项，会让输入增大，使得水塔水位可以大于0.8，渐渐到达目标的1.0.


微分控制算法: 减少逼近时震荡。

换另外一例: 刹车情况。
平稳的驾驶车辆，

  • 发现前面有红灯时, 提前几十米就放松油门并踩刹车(为使得行车平稳)。
  • 刹车过程, error是越来越小的.
  • error非常小(接近停车线)时, 则用力踩刹车, 使车辆停准。

整个过程可以看做一个加入“微分控制”的策略。

离散情况，, t时刻 和 t-1 时刻 error的差，即:

\[\large u= kd \times (error(t) - error(t-1) ), \ kd \text{ 是 误差微分 的 比率 }, \ \text{ 离散情况的微分 其实用"两个error相减" \]

\(\large (error(t) - error(t-1) )\)(微分控制项) 一定是"负数"(刹车过程的error是越来越小的)，
加入这个“负数项”的作用, 是为及时刹车, 防止汽车过线。

常识上理解，越靠近停车线，越应该注意踩刹车不过线，
所以微分项的作用，可理解为刹车:
当车离停车线很近 并且 车速还很快时，
这个微分项(负数)的"绝对值"会很大, 代表应该“用力踩刹车”才能车停。

换“水塔加水”例，
当发现水塔当前水位快要接近目标水位1时，加入微分项，防止给水塔水位超过1米高度。



posted @ 2025-04-08 07:47  abaelhe  阅读(19)  评论(0)    收藏  举报