SciTech-Mathmatics-Mathmatical Analysis-Series:Taylor Series Approxmation:特例$\large ln(1+x)$ + 收敛半径: 几何级数 + Abel的边界 + Julia(茱莉亚)集合 + 分形几何
SciTech-Mathmatics-Mathmatical Analysis-Series
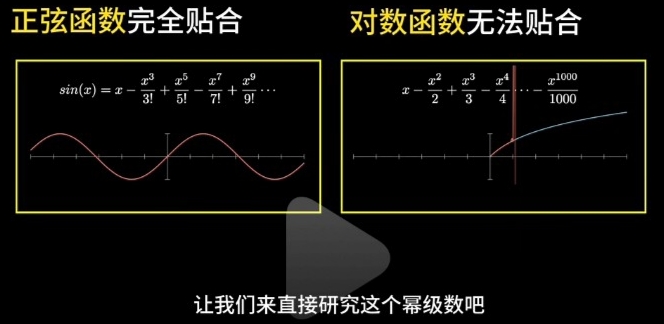
Taylor Series Approxmation:特例\(\large ln(1+x)\) + 收敛半径
: 几何级数 + Abel的边界 + Julia(茱莉亚)集合 + 分形几何
阿贝尔的边界,朱利亚集,以及那些莫名的美丽
https://v.douyin.com/iPSLWsjs/
 |
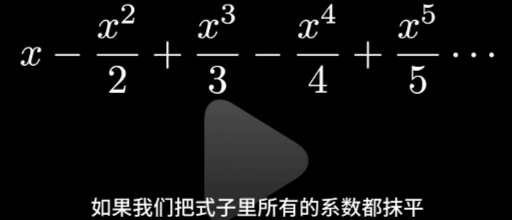 |
 |
 |
得到: 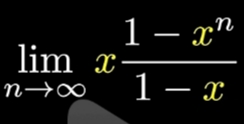
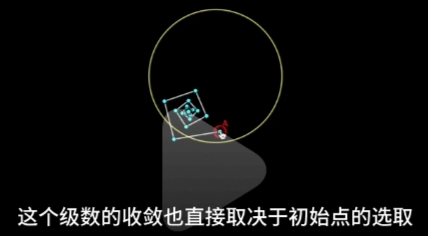
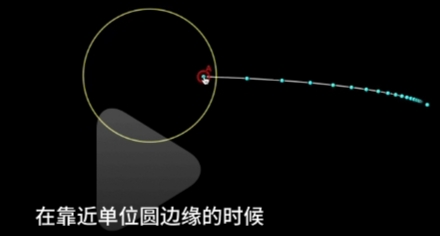
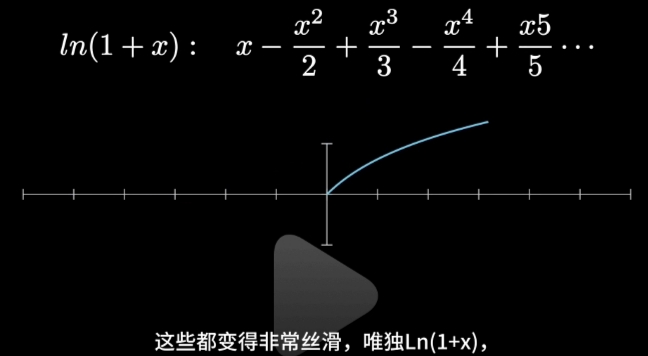
“几何级数”收敛是有条件的: 只有当\(\large |x| < 1,\ 即 x \in (-1, +1)\) , 这个级数才有意义。
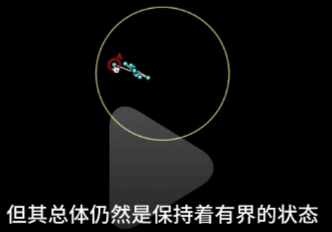
如果我们把 \(\large x\) 看成是复数, 那么我们可以把"前n项级数加总得到的级数总和点画出来":
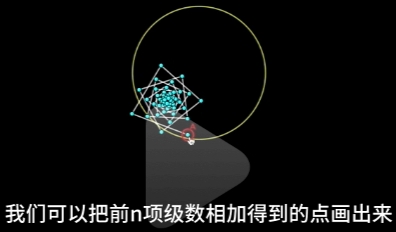 |
 |
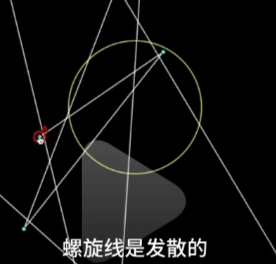
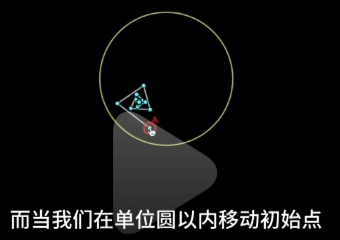
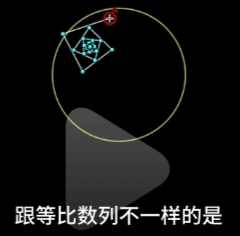
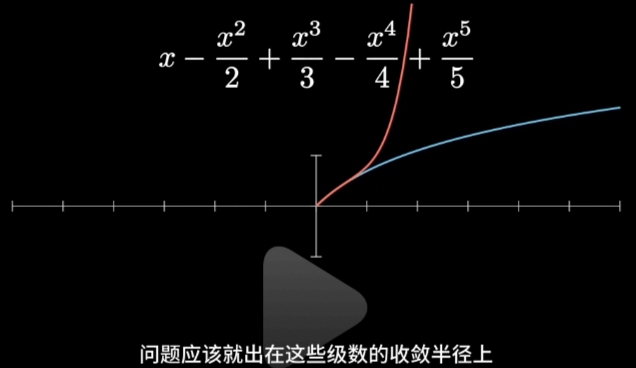
Abel 的收敛半径
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
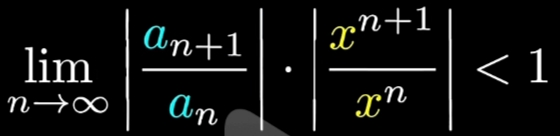
达郎贝尔 审敛法
 |
 |
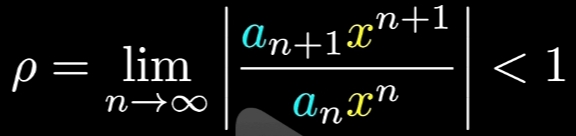 |
|
 |
 |
 |
|
 |
 |
  |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号