SciTech-Mathmatics-Probability+Statistics-Conditional Probability + Bayes Theorem+App.: 条件概率+Bayes原理及应用:广告邮件分类
SciTech-Mathmatics-Probability+Statistics
Conditional Probability + Bayes Formula: Application:
Conditional Probability(条件概率)
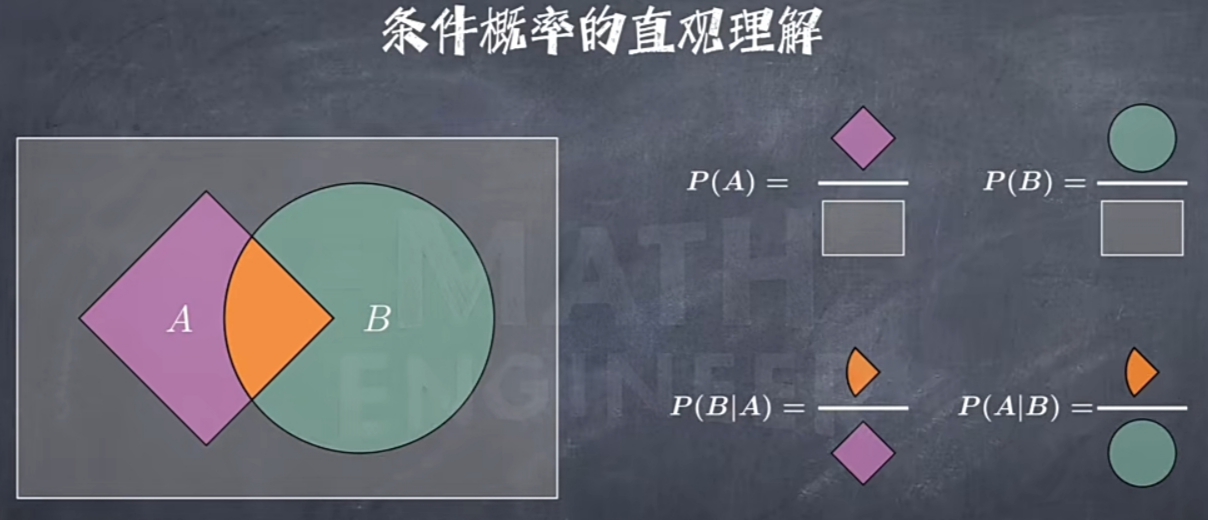
Bayes Formula
\[\large \begin{array}{lll}\\
\bm{ P(A | B) } =\dfrac{ \bm{ P(B | A) } P(A) } { P(B) } =\dfrac{ \bm{ P(B | A) } P(A) } { \overset{n}{ \underset{k=1}{ \sum}} P( A_k \cap B) } =\dfrac{ \bm{ P(B | A) } P(A) } { \overset{n}{ \underset{k=1}{ \sum} } { P(A_k) P(B | A_k) } } \\
\\
\downarrow \bm{ existing\ a \ partition } \text{ of } A : if \ P(B|A_k) \text{ is available for each } k \\
\\
\bm{ P(A_i | B) } =\dfrac{ \bm{ P(B | A_i) } P(A_i) } { P(B) } =\dfrac{ \bm{ P(B | A_i) } P(A_i) } { \overset{n}{ \underset{k=1}{ \sum} } { P(A_k \cap B) } } =\dfrac{ \bm{ P(B | A_i) } P(A_i) } { \overset{n}{ \underset{k=1}{ \sum} } { P(A_k) P( B | A_k) } } \\
\end{array}\]
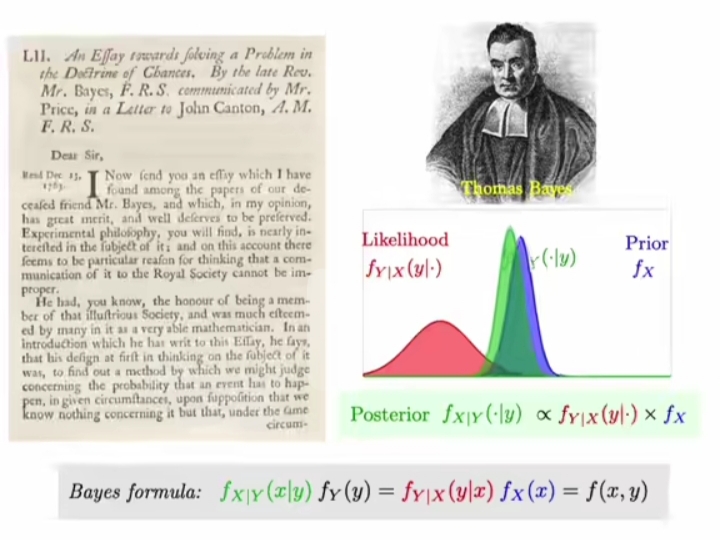

举例:
收到所有信件,出现“收入”词组的概率
Statistics of Samples
\[\large \begin{array}{lll}\\
\text {所有信件} \begin{cases} \\
\overset{ \bm { P(A_1) = \frac{3}{8} } }{ \bm{ 广告信件 } } & \begin{cases}
& \overset{ \bm{ P(K_1) } = \frac{2}{3} } { 出现\bm{广告}词组 } \ : \bm { P(K_1|A_1) } = \frac{2}{8} \\
& \overset{ \bm{ P(K_2) } = \frac{1}{3} } { 没有\bm{广告}词组 } \ : \bm { P(K_2|A_2) } = \frac{1}{8} \\
\end{cases} \\
\overset{ \bm { P(A_2) = \frac{5}{8} } }{ \bm{ 正常信件 } } & \begin{cases}
& \overset{ \bm{ P(K_1) } = \frac{1}{5} } { 出现\bm{广告}词组 } \ : \bm { P(K_1|A_2) } = \frac{1}{8} \\
& \overset{ \bm{ P(K_2) } = \frac{4}{5} } { 没有\bm{广告}词组 } \ : \bm { P(K_2|A_2) } = \frac{4}{8} \\
\end{cases} \\
\end{cases} \\
\end{array} \]
Statistical Inference based on above Statistics and its Samples
- 现在,收到一份信件,并且有 $\large \bm{广告}词组 $ , 则此信是“广告信”的概率是?
\[\large \begin{array}{lll}\\
\text {有 $\large \bm{广告}词组 $} \begin{cases} \\
\bm{ 广告信 } : \bm { P(A_1 | K_1) } = \bm{ \frac{2}{3} } \leftarrow \dfrac{ \frac{2}{8} } { \frac{2}{8} + \frac{1}{8} } =\dfrac{ \bm{ P(K_1 | A_1) } P(A_1) } { \overset{n}{ \underset{i=1}{ \sum} } { P(A_1) P( K_i | A_1) } } \\
\bm{ 正常信 } : \bm { P(A_2 | K_1) } = \bm{ \frac{1}{3} } \leftarrow \dfrac{ \frac{1}{8} } { \frac{2}{8} + \frac{1}{8} } =\dfrac{ \bm{ P(K_1 | A_2) } P(A_2) } { \overset{n}{ \underset{i=1}{ \sum} } { P(A_2) P( K_i | A_2) } } \\
\end{cases} \\
\end{array} \]
可以看到信件有 $\large 出现\bm{广告}词组 $ 出现为前提,
是“广告信件”的概率由:
- 先验的样本统计概率 $\large \bm { P(A_1) =P(K_1|A_1)+P(K_2|A_1) = \frac{3}{8} } $
上升到:
- 后验的样本更新概率 $\large \bm { P(A_1 | K_1) = \frac{2}{3} } $
导致样本空间的概率分布变更的原因:
系统原因(需要更新统计量?或新验证模型?):
- “前提条件的设置/完备”导致“归一化概率”的“样本空间改变”;
- “正交概率分布”的“样本集”的“完全分布”变更导致;
- 外部因素影响“正交概率分布”的“部分占比”变更导致;
随机因素(需要更大的样本空间以抵消误差因素?):
- 因为一些随机因素引发的Error(误差).
-
总之“Prior维度集合的Partition”与“Posterior维度集合的Partition”的“正交集合笛卡尔积”的“条件概率分布”的“参数”或“配比”发生了变更;
-
实例是:
- 在“Posterior(后验)”时,能对event(事件的)设置/完备的“前提条件”越来越多,就需要 Revise 其对应的Probability. 以上例:判断信新收到的一份信,是“广告邮件”的概率,可以由信的“关键词向量”丰富程度来确定。
- 总由$\large Population $ 或 $\large Samples $ 统计得到的“Prior维度”的所有“Statistics(统计量)”;
而 $\large Population $ 或 $\large Samples $ 可能因为时间或发展变化而更新,因此统计得到的“Prio
r维度”的所有“Statistics(统计量)”也会变更;
以上面“广告信比例”为例:
"样本空间" 越来越大(接收到的所有有效信件越来越多),"AI系统"周期性更新"样本空间"的"统计量",包括:- \(\large P(A1)\) : “全量样本空间”,统计出 $ \bm{ 广告信 } $ 的概率;
- \(\large P(A2)\) : “全量样本空间”,统计出 $ \bm{ 正常信 } $ 的概率;
- \(\large P(K1 | A1)\) : $ \bm{ 广告信 } $ 集合,出现 $\large \bm{广告}词组 $ 的概率;
- \(\large P(K1 | A2)\) : $ \bm{ 正常信 } $ 集合,出现 $\large \bm{广告}词组 $ 的概率;
- \(\large P(K2 | A1)\) : $ \bm{ 广告信 } $ 集合,没有 $\large \bm{广告}词组 $ 的概率;
- \(\large P(K2 | A2)\) : $ \bm{ 正常信 } $ 集合,没有 $\large \bm{广告}词组 $ 的概率;
前提是“Prior维度集合的Partition”与“Posterior维度集合的Partition”有“正交集合笛卡尔积”的“条件概率分布”;
对上例:
- Prior维度集合的Partition 是: $\large P(广告信) P(正常) $
的“正交集合积”的“条件概率分布”即:
计算出“Posterior后验”后验
(由A的Partition $\large \bm { P(K_1 | A_1) } $ 和 $\large \bm { P(K_1 | A_2) } $ 可计算出两维度的“共现(交集)” 概率) $\large \bm { P(K_1 | A_1) } $ ) P(K_1|A_1)+P(K_2|A_1)
Revise the probability of \(\large P(K1 | A_i)\)
即
那么根据越多的“关键词”的“后验”概率,判断得出正确结果的概率就越大。
p垃圾邮件”收入,赚钱…成功?)
∝
p收入”|“垃圾邮件”)p(赚钱”|垃圾邮件),p成功”|“垃圾邮件?)
pC正常邮件!收入“赚钱”…成功)
∝
pC收入“正常邮件PT赚钱”|“正常邮件).pC成功”“正常邮件?




