PID算法图形 python

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139

# -*- coding: utf-8 -*-     class PID:     def __init__(self, P=0.2, I=0.0, D=0.0):         self.Kp = P         self.Ki = I         self.Kd = D         self.sample_time = 0.00         self.current_time = time.time()         self.last_time = self.current_time         self.clear()       def clear(self):         self.SetPoint = 0.0         self.PTerm = 0.0         self.ITerm = 0.0         self.DTerm = 0.0         self.last_error = 0.0         self.int_error = 0.0         self.windup_guard = 20.0         self.output = 0.0       def update(self, feedback_value):         error = self.SetPoint - feedback_value         self.current_time = time.time()         delta_time = self.current_time - self.last_time         delta_error = error - self.last_error         if (delta_time >= self.sample_time):             self.PTerm = self.Kp * error  # 比例             self.ITerm += error * delta_time  # 积分             if (self.ITerm < -self.windup_guard):                 self.ITerm = -self.windup_guard             elif (self.ITerm > self.windup_guard):                 self.ITerm = self.windup_guard             self.DTerm = 0.0             if delta_time > 0:                 self.DTerm = delta_error / delta_time             self.last_time = self.current_time             self.last_error = error             self.output = self.PTerm + (self.Ki * self.ITerm) + (self.Kd * self.DTerm)       def setKp(self, proportional_gain):         self.Kp = proportional_gain       def setKi(self, integral_gain):         self.Ki = integral_gain       def setKd(self, derivative_gain):         self.Kd = derivative_gain       def setWindup(self, windup):         self.windup_guard = windup       def setSampleTime(self, sample_time):         self.sample_time = sample_time     import time import matplotlib   matplotlib.use("TkAgg") import matplotlib.pyplot as plt import numpy as np from scipy.interpolate import make_interp_spline         def test_pid(P=0.2, I=0.0, D=0.0, L=100):           pid = PID(P, I, D)       pid.SetPoint = 0.0     pid.setSampleTime(0.01)       END = L     feedback = 0       feedback_list = []     time_list = []     setpoint_list = []       for i in range(1, END):         pid.update(feedback)         output = pid.output         # print(output)         if pid.SetPoint > 0:             feedback += output  # (output - (1/i))控制系统的函数         if 9 <= i <= 40:             pid.SetPoint = 1         elif i > 40:             pid.SetPoint = 0.5           time.sleep(0.01)           feedback_list.append(feedback)         setpoint_list.append(pid.SetPoint)         time_list.append(i)       time_sm = np.array(time_list)     time_smooth = np.linspace(time_sm.min(), time_sm.max(), 300)     feedback_smooth = make_interp_spline(time_list, feedback_list)(time_smooth)     plt.figure(0)     plt.plot(time_smooth, feedback_smooth)     plt.plot(time_list, setpoint_list)       plt.xlabel('time (s)')     plt.ylabel('PID (PV)')     plt.title('TEST PID {}/{}/{}'.format(P, I, D))       plt.xlim((0, L))     plt.ylim((-0.5, 2))       plt.grid(True)     # plt.show()     plt.savefig('./images/TEST PID {}-{}-{}.jpg'.format(P, I, D))     plt.close()     if __name__ == "__main__":     test_pid(1.2, 1.0, 0.001, L=50)     test_pid(1.2, 1.0, 0, L=50)     test_pid(1.2, 0, 0, L=50)       test_pid(0.8, 1.0, 0.001, L=50)     test_pid(0.8, 1.0, 0, L=50)     test_pid(0.8, 0, 0, L=50)       test_pid(0.2, 0.0, 0.001, L=50)     test_pid(0.2, 0.0, 0, L=50)     test_pid(0.2, 0, 0, L=50)       test_pid(0.8, 0, 0.001, L=50)     test_pid(1.2, 0, 0.001, L=50)       test_pid(0.7, 0.8, 0.001, L=50)       test_pid(0.8, L=50)

　　

 

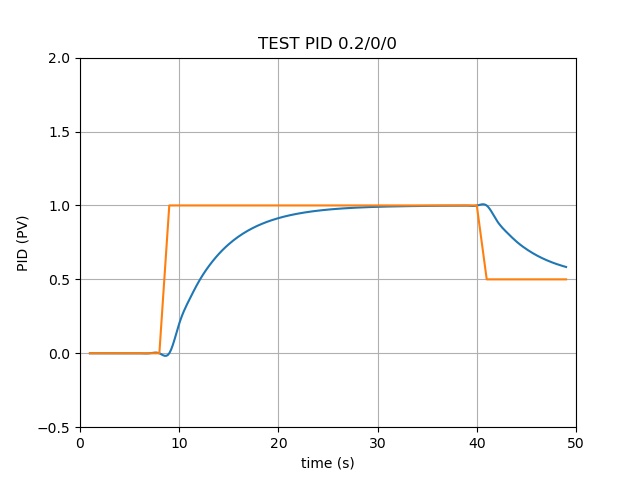
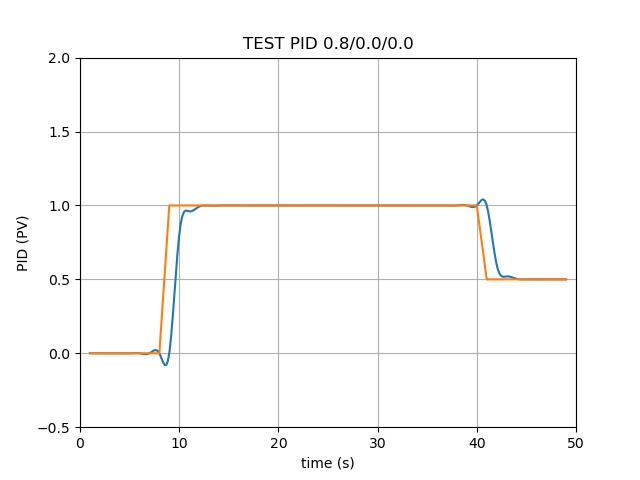
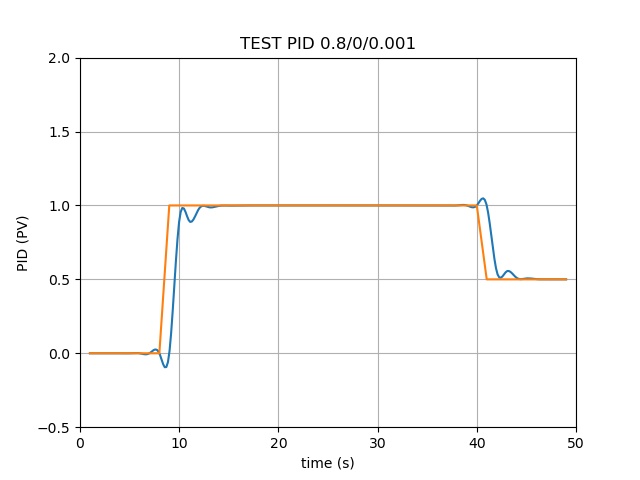
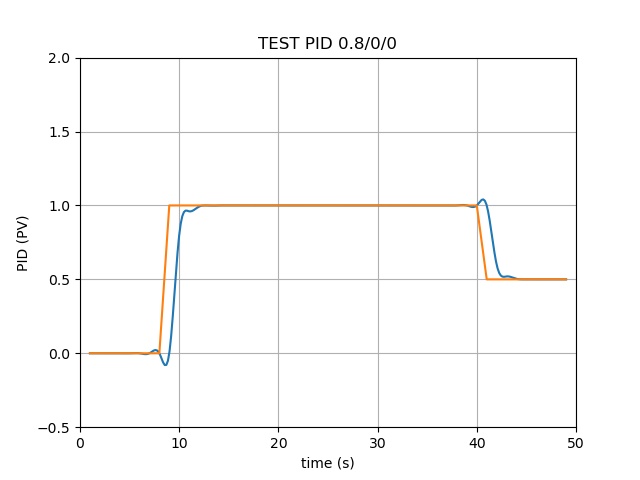
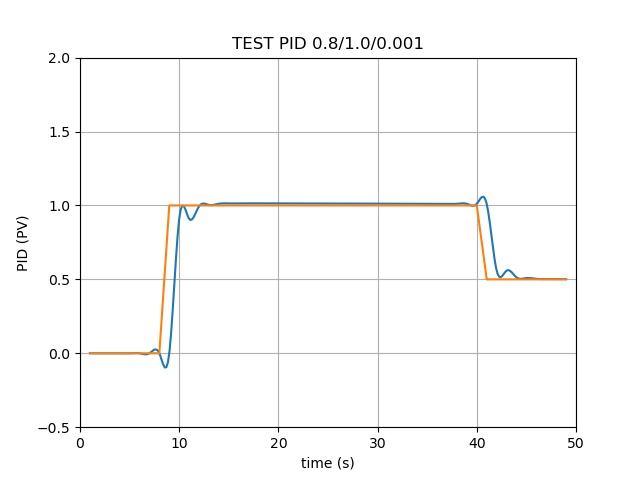
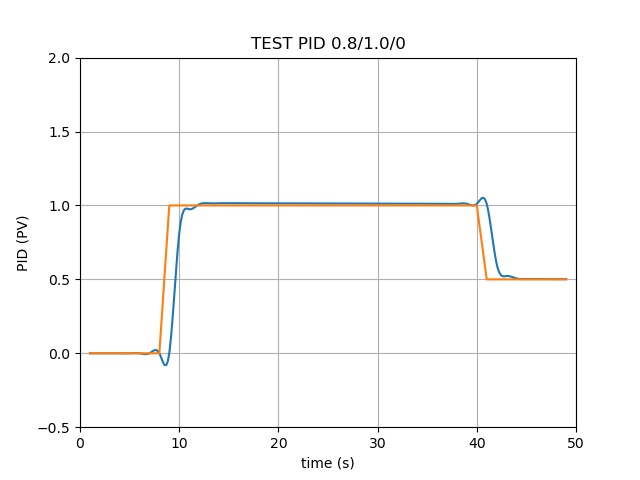
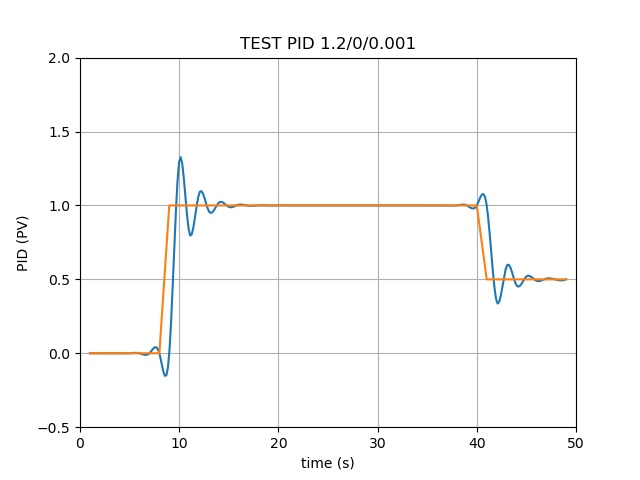
模拟了电动机电压的输出：

• 从0秒开始到第9秒，要求输出电压为0V；
• 从第10秒开始到第40秒，要求输出电压为1V；
• 从第41秒开始到第50秒，要求输出电压为0.5V

橘黄色线代表上述需求（理想输出电压）

绿色线为PID算法输出带反馈积分的输出电压

看得到P（比例）部分 是一个最重要的参数、I（积分）部分能让两条线完全重合（可能过于理想，有待验证）、D（微分）部分会对电压产生微调的上下波动影响

PID算法的参数看来是能够影响元器件寿命的