第2章信息的表示和处理

三种重要的数字表示：

无符号（unsigned）。基于传统的二进制表示法，表示大于或等于零的数字。
补码（two's-complement）。表示有符号整数的最常见方式。
浮点数（floating-point）。表示实数的科学记数法的以 2 为基数的版本。
计算机的表示法是用有限数量的位来对一个数字编码。

整数运算和浮点数运算有完全不同的数学属性。

二者在处理数字表示有限性的方式不同
浮点数运算虽然可以表示一个较大的数学范围，但是这种表示只是近似（所以浮点运算是不可结合的）。而整数运算能够精确表示，虽然只能表示一个较小的数学范围。

关于本章乃至下一章都是基于一组核心的数学原理，从编码的基本定义开始，然后得到一些属性

可表示的数字的范围
这些数字的位级表示
算术运算的属性

通过直接操作数字的位级表示会得到几种进行算术运算的方式。理解这些技术对理解编译器产生的机器级代码很重要。

程序员需要对计算机运算与更为人熟悉的整数和实数运算之间的关系有清晰的理解。

2.1 信息存储

大多数计算机使用 8 位的字节（byte）作为最小的可寻址内存单位。机器级程序将内存视为一个巨大的字节数组（虚拟内存（virtual memory）），其内存的每个字节都由一个唯一的数字标识，这个所有可能地址集合称为虚拟地址空间（virtual address memory）。该地址集合仅是展示给机器级程序的概念性映像。

2.1.1 十六进制表示法

如何表示一个字节？采用二进制，其值域为 \(00000000_2\sim11111111_2\) ，但是太冗长了。
采用十进制，其值域为 \(0_10\sim255_10\) ，但是与位模式的互相转换很麻烦。所以，通常使用十六进制（hexadecimal，hex）数表示位模式，其值域为 \(0\sim F\) 。

对于十六进制与十进制的转换，窍门是记住 A（10）、C（12）和 F（15）的十进制值。通过十进制值也很好的转换为二进制值（4 位为一组）。

十进制转二进制，则记住 8（1000）、4（0100）和 2（0010）这三个数，通过将给定数化为这三个数的加减序列得到二进制序列。

同时，如何是十六进制转二进制，则还需记住 A（1010）、C（1100）和 E（1110）这三个数，例如，0x173a4c：

hex:    1    7    3    a    4    c
bin: 0001 0111 0011 1010 0100 1100

反过来，如果是二进制数转十六进制数，以 4 位为一组（总数不满足 4 的倍数，左侧加零补全）。例如，11,1100,1010,1101,1011,0011

bin: 0011 1100 1010 1101 1011 0011
hex:    3    c    a    d    b    3

十六进制和十进制的转换，一般是对 16 进行出发和乘法运算。比如，十进制转十六进制，那么 \(x_{10}=16*q+r\) ，进行不停的演算，得到的余数 r 作为低位。

反过来，十六进制转十进制，则用相应的 16 的幂乘以每位的十六进制值。

2.1.2 字数据大小

每个计算机都有一个字长（word size，Byte）, 用于指明指针数据的标称大小（nominal size）。字长决定的最重要系统参数是虚拟地址空间的最大大小，对于一个字长为 \(\omega\) 位的机器而言，其虚拟地址空间的范围为 \(0\sim 2^{\omega}-1\) 。

备注

位（Bit）。表示一个二进制数 0 或 1。

字节（byte）。一个字节由 8 位组成。

字长（Byte）。用于表示机器的虚拟地址。不同机器具有不同字长，32 位机器上一个字长表示 4 字节，64 位机器上一个字长表示 8 字节。

字（Word）。2 字节表示一个字，数据存储和数据处理单元。

C 语言支持多种整数和浮点数格式。

其中 char 用于表示单独的字节，存储单个字符，但是也可以存储整数值。
为了避免依赖“典型”大小和不同编译器设置带来的变化，C99 中引入 int32_t 和 int64_t，二者表示 4 字节和 8 字节，不随编译器和机器设置变化。
大多数数据类型都编码位有符号数值，除非有 unsigned 前缀。但是 char 例外，C 标准并不保证其为有符号类型（尽管大多数编译器和机器视为有符号类型）。
C 语言标准对不同数据类型的数字范围设置了下界，但是并没有明确上界。
指针使用程序的全字长。

C 声明和对应字节数：

有符号	无符号	32 位	64 位
`[signed] char`	`unsigned char`	1	1
`short`	`unsigned short`	2	2
`int`	`unsigned`	4	4
`long`	`unsigned long`	4	8
`int32_t`	`uint32_t`	4	4
`int64_t`	`uint64_t`	8	8
`char *`		4	8
`float`		4	4
`double`		8	8

2.1.3 寻址和字节顺序

几乎在所有的机器上，多字节对象都被存储为连续的字节序列，对象的地址位所使用字节中最小的地址。

排列表示一个对象的字节有两个通用的规则，

在内存中按照从最低有效字节到最高有效字节的顺序存储对象，最低有效字节在前面的方式称为小端法（little endian）
按照从最高有效字节到最低有效字节的顺序存储对象，最高有效字节在前面的方式称为大端法（big endian）

通常情况下，大多数现代计算机和操作系统，包括Linux，都是使用小端法。大端法多用于网络传输和某些特定类型的文件格式中。

判断系统采用那种模式，可以运行下面程序：

#include <stdio.h>

int main() {
    unsigned int x = 1;
    char *c = (char*)&x;
    if (*c) { // c==01
        printf("小端法\n");
    } else {  // c==00
        printf("大端法\n");
    }
    return 0;
}

在小端法系统中，最低有效字节（LSB）存储在最低的地址上，所以如果系统是小端法， *c 将会是 01 ，条件 *c 为真，程序打印出"小端法"。在大端法系统中，最高有效字节（MSB）存储在最低的地址上，所以如果系统是大端法， *c 将会是 00 ，条件 *c 为假，程序打印出"大端法"。

补充

强制类型转换并不会改变真实的指针，它们只是告诉编译器以新的数据类型来看待被指向的数据。

2.1.4 表示字符串

C 语言中字符串被编码为一个 null 字符（ \0 ）结尾的字符数组，每个字符由某个标准编码（如 ASCII）表示。

文本数据比二进制数据具有更强的平台独立性，因为在使用 ASCII 码作为字符码的任何系统上都将得到相同的结果，与字节顺序和字大小规则无关。

补充

Unicode“统一字符集”。支持广泛的语言种类，使用 32 位来表示字符，但是常见的字符只需要 1 到 2 各字节，所以标准 ASCII 字符的字节序列与 UTF-8 表示的是一样的。

UTF，Unicode Transformation Format.

2.1.5 表示代码

计算机系统的一个基本概念就是，从机器的角度来看，程序仅仅只是字节序列。机器没有关于原始源程序的任何信息，除了可能有些用来帮助调试的辅助表以外。

2.1.6 布尔代数简介

布尔通过将逻辑值 TRUE（真）和 FALSE（假）编码为二进制值 1 和 0，能够设计一种代数，以研究逻辑推理的基本原则。

布尔运算～
- 逻辑运算 NOT。
- 命题逻辑 \(\lnot\) 。
布尔运算 &
- 逻辑运算 AND 。
- 命题逻辑 \(\land\) 。
布尔运算 |
- 逻辑运算 OR。
- 命题逻辑 \(\lor\) 。
布尔运算 ^
- 逻辑运算 EXCLUSIVE-OR（异或）。
- 命题逻辑 \(\oplus\) 。

同时，可以将布尔运算扩展到位向量的运算，定义成参数的每个对应元素之间的运算。

补充

&对 | 的分配律：a&(b|c)=(a&b)|(a&c)

|对&的分配律：a|(b&c)=(a|b)&(a|c)

以及逆元：(a^b)a=b

位向量还有一个很有用的应用就是表示有限集合，例如：a=[0110 1001]，从右往左读，当值为 1 时，记录其所在索引，即 a 表示的集合 A ={0,3,5,6}；同理，b=[0101 0101]表示的集合为 B={0,2,4,6}。布尔运算的|和&表示集合的并集和交集，^表示补集。那么 a&b= \(A \cap B\) ={0,6}=[0100 0001]。

2.1.7 C 语言中的位级运算

确定一个位级表达式的结果最好的方法，就是将十六进制的参数扩展到二进制表示并执行二进制运算，然后在转换为十六进制。

位级运算的一个常见用法就是实现掩码运算，这里掩码是一个位模式，表示从一个字中选出的位的集合。比如，掩码 0xFF（最低的 8 位为 1，其余位为 0）与其他值进行&运算，无论该值为多少，最后都仅会保留 8 位最低有效位。

2.1.8 C 语言中的逻辑运算

逻辑运算认为所有非零的参数都表示 TRUE，而参数 0 表示 FALSE。逻辑运算还有一个特点，当第一个参数求值就能确定表达式的结果，那么逻辑运算符就不会对第二个参数求值，即短路特性。

2.1.9 C 语言中的移位运算

C 表达式 x<<k，表示 x 向左移动 k 位，丢弃最高的 k 位，在右端补齐 k 个 0。

C 表达式 x>>k，表示 x 向右移动 K 位，其中按照机器支持的形态分为

逻辑右移
- 在左端补 k 个 0。
算术右移
- 在左端补 k 个最高有效位的值。

几乎所有的编译器/机器组合都对有符号数使用算术右移，对无符号数，使用逻辑右移。

对于一个由 \(\omega\) 组成的数据类型，当位移量 \(k \geq \omega\) 时，位移量通过 \(k \mod \omega\) 得到。不过 C 程序对此没有保证，所以应该保持位移量小于待移位值的位数。

2.2 整数表示

2.2.1 整型数据类型

整型数据类型，表示有限范围的整数。C 语言标准定义了每种数据类型必须能够表示的最小的取值范围。

补充

C 和 C++ 都支持有符号（默认）和无符号数，Java 只支持有符号数。

2.2.2 无符号数的编码

对无符号数编码的定义，有向量 \(\vec{x}=[x_{\omega-1},x_{\omega-2},...,x_0]\) ：

\[B2U_{\omega}({\vec{x}})\overset{.}{=}\sum_{i=0}^{\omega-1}x_{i}2^{i} \]

其中， \(B2U_w\) 函数是 Binary to Unsigned 的缩写，长度为 \(\omega\) 。 \(\omega\) 位所能表示的值的范围，最小值用位向量[00.... 0]表示，也就是整数 0；最大值用位向量[111.... 1]表示，也就是整数值 \(UMaX_\omega\overset{.}{=}\sum_{i=0}^{\omega-1}2^i=2^\omega-1\) 。因此，函数 \(B2U_w\) 能够被定义为一个映射 \(B2U_\omega\) ： \(\{0,1\}^{\omega} \rightarrow \{0,...,2^\omega-1\}\) ，需要注意到函数 \(B2U_w\) 是一个双射。

2.2.3 补码编码

补码的关键特征就是将字的最高有效位解释为负权（negative weight）。对补码编码的定义，有向量 \(\vec{x}=[x_{\omega-1},x_{\omega-2},...,x_0]\) ：

\[B2T_{\omega}(\vec{x})\ \overset{.}{=}-x_{\omega-1}2^{\omega-1}+\sum_{i=0}^{\omega-2}x_{i}2^{i} \]

其中， \(B2T_\omega\) 函数是 Binary to Two's-complement 的缩写，补码所能表示的最小值的位向量为[1000.... 0]，其整数值为 \(TMin_\omega\overset{.}{=}-2^{\omega-1}\) ，最大值的位向量为[0111... 1]，其整数值为 \(TMax_\omega\overset{.}{=}\sum_{i=0}^{\omega-2}2^i=2^{\omega-1}-1\) ，同样补码编码也具有唯一性，函数 \(B2T_w\) 是一个双射。对于每个数 x, 满足 \(TMin_{\omega}\leq x \leq TMax_{\omega}\) ，则 \(T2B_\omega\) 是 x 的（唯一的） \(\omega\) 位模式。

需要注意到：

\(|TMin|=|TMax|+1\) ,即最小负数并没有与之对应的正数，因为 0 是非负数，意味着能表示的整数(1，127) 比负数（-1，128）少一个。
\(|UMax|=|TMax|+1\) 。

C 语言标准并没有要求要用补码形式来表示有符号整数，但是几乎所有的机器都是这么做的。C 语言标准只指定了每种数据类型的最小范围，而不是确定的范围。

补充

确定宽度类型的带格式打印需要使用宏，以于系统相关的方式扩展为格式串。使用宏能保证：不论代码是如何被编译的，都能生成正确的格式字符串。

有符号数还有两种标准的表示方法：

反码（Ones' Complement）：除了做高有效位的权重为 \(-(2^{\omega-1}-1)\) 外，其他与补码是一致的。补码等于反码+1。

\[B2O_{\omega}(\vec{x})\ \overset{.}{=}-x_{\omega-1}(2^{\omega-1}-1)+\sum_{i=0}^{\omega-2}x_{i}2^{i} \]

原码（Sign-Magnitude）：最高有效位是符号位，用来确定剩下的位应该取负权还是正权。

\[B2S_{\omega}(\vec{x})\ \overset{.}{=}(-1)^{x_{\omega-1}}+\sum_{i=0}^{\omega-2}x_{i}2^{i} \]

二者对于表示数字 0 有两种不同的编码方式，都把[000……0]表示+0。但是对于-0，反码表示为[111……1]，原码表示为[1000……0]。由于上述两种方式对 0 有不同的编码解释，所以现代机器上几乎都用补码表示。

补充

术语补码（Two's complement）和术语反码（Ones'complement）来源于以下情况。

补码：对于非负数 \(x\) ，我们用 \(2^{\omega}-x\) 计算 \(-x\) 的 \(\omega\) 位表示。表示这里只有一个 2（Two's）。

反码：用 \([1111……1]-x\) 计算 \(-x\) 的反码表示。这里有许多 1，所以用“Ones' ”表示。

2.2.4 有符号数和无符号数之间的转换

强制类型转换的结果保持位值不变，只是改变解释这些位的方式。

对于大多数 C 语言的实现，处理同样字长的有符号数和无符号数之间相互转换的一般规则是：数值可能会改变，但是位模式不变。用更数学化的方式描述这个规则：

例如：函数 \(T2U_\omega\) ，定义为：

\[T2U_{\omega(x)} \overset{.}{=}B2U_{\omega}(T2B_{\omega}) \qquad x \in [TMin,TMax] \]

得到 \(0\sim UMax_{\omega}\) ，这两个数具有相同的位模式，除了参数是无符号的，结果以补码表示。

补码转无符号数：

\[T2U_{\omega}(x) = \begin{cases} x+2^{\omega}, &x<0 \\ x, &x\geq0 \\ \end{cases} \]

无符号转补码：

\[U2T_{\omega}(x)= \begin{cases} u, &u\leq TMax_{\omega} \\ u-2^{\omega}, &u>TMax_{\omega} \end{cases} \]

补充

对于在范围 \(0\leq x \leq TMax_{\omega}\) 之内的值 \(x\) 而言，我们得到 \(T2U_{\omega}(x)=x\) 和 \(U2T_{\omega}(x)=x\) ，在此范围外则需要加上或减去 \(2^{\omega}\) 。

此外，我们还可以发现两个现象：1. 最靠近 0 的负数映射为最大的无符号数；2. 最小的负数映射为一个刚好在补码正数范围之外的无符号数。

2.2.5 C 语言中的有符号数与无符号数

C 语言中，通常大多数数字被认为是有符号的。要创建一个无符号常量，必须加上后缀字符“u”或者“U”。例如，“123456u”。

在进行无符号和有符号转换时，C 语言虽然没有精确规定应如何进行这种转换，但是大多数系统遵循的原则是底层位表示不变。

当执行一个运算，其中包含有有符号数和无符号数，那么 C 语言会隐式将有符号数强制类型转换为无符号数，并假设这两个数都是非负的。

2.2.6 扩展一个数字的位表示

无符号扩展

要将一个无符号数转换为一个更大的数据类型，我们只需要简单地在表示的开头添加 0。这种运算被称为零扩展（zero extension）。

表示原理：定义宽度为 \(\omega\) 的位向量 \(\vec{u}=[u_{\omega-1}, u_{\omega-2}, ..., u_0]\) 和宽度为 \(\omega'\) 的位向量 \(\vec{u}'=[0, ..., 0, u_{\omega-1}, u_{\omega-2}, ..., u_0]\) ，其中 \(w'>w\) 。则 \(B2U_{\omega}(\vec{u})=B2U_{\omega'}(\vec{u}')\) 。

补码数的符号扩展

将补码数字转换为一个更大的数据类型，可以执行一个符号扩展（sign extension），在表示中添加最高有效位的值。

表示原理：定义宽度为 \(\omega\) 的位向量 \(\vec{x}=[x_{\omega-1}, x_{\omega-2}, ..., x_0]\) 和宽度为 \(\omega'\) 的位向量 \(\vec{x}'=[x_{\omega-1}, x_{\omega-1}, ....,x_{\omega-1}, u_{\omega-2}, ..., x_0]\) ，其中 \(w'>w\) 。则 \(B2U_{\omega}(\vec{x})=B2U_{\omega'}(\vec{x}')\) 。

对补码的扩展就是左侧加上 n 个符号位值，那么我们尝试进行推导：

\[B2T_{\omega+k}([x_{\omega-1}, x_{\omega-1}, ....,x_{\omega-1}, u_{\omega-2}, ..., x_0])=B2T_{\omega}([x_{\omega-1}, x_{\omega-2}, ..., x_0]) \]

对 k 进行归纳，那么只需证明符号扩展 1 位就能保持数值的不变，那么符号扩展任意位都能保持这种属性，因此证明变为：

\[\begin{align*} B2T_{\omega+k}([x_{\omega-1}, x_{\omega-1}, u_{\omega-2}, ..., x_0])&=B2T_{\omega}([x_{\omega-1}, x_{\omega-2}, ..., x_{0])} \end{align*} \]

展开左侧表达式：

\[\begin{align*} B2T_{\omega+k}([x_{\omega-1}, x_{\omega-1}, u_{\omega-2}, ..., x_0])&=-x_{\omega-1}2^{\omega}+\sum\limits_{i=0}^{\omega-1}x_{i2^i}\\\\ &=-x_{\omega-1}2^{\omega}+x_{\omega-1}2^{\omega-1}+\sum\limits_{i=0}^{\omega-2}x_i2^i\\ &=-x_{\omega-1}(2^{\omega}-2^{\omega-1})+\sum\limits_{i=0}^{\omega-2}x_i2^i\\ &=-x_{\omega-1}2^{\omega-1}+\sum\limits_{i=0}^{\omega-2}x_i2^i\\ &=B2T_{\omega}([x_{\omega-1}, x_{\omega-2}, ..., x_0]) \end{align*} \]

综上所述，加上一个权值位 \(-2^{\omega}\) 的位，和将一个权值位 \(-2^{\omega-1}\) 的位取反，两项运算的综合效果就会保持原始的数值。

2.2.7 截断数字

减少一个数字的位数，那么会发生截断效果（高位截断），例如 [C_P56](https://github.com/Free-Aaron-Li/learning_csapp/blob/master/PartI/ChapterII/code/C_P.cpp #L74 )。

截断无符号数

令 \(\vec{x}\) 等于向量 \([x_{\omega-1}, x_{\omega-2}, ...,x_0]\) ，而 \(\vec{x}'\) 是将其截断位 k 位的结果： \(\vec{x}'=[x_{k-1}, x_{k-2}, ..., x_0]\) 。令 \(x=B2U_{\omega}(\vec{x}),x'=B2U_{k}(\vec{x}')\) 。则 \(x'=x\ mod\ 2^k\) 。

尝试推导：

\[\begin{align*} B2U_{\omega}([x_{\omega-1}, x_{\omega-2}, ..., x_{0}])\ mod\ 2^{k} &=\left[\sum\limits_{i=0}^{\omega-1} x_{i}2^{i}\right]\ mod\ 2^{k}\\ &=\left[\sum\limits_{i=0}^{k-1} x_{i}2^{i}\right]\ mod\ 2^{k}\\ &=\sum\limits_{i=0}^{k-1} x_{i}2^{i}\\ &=B2U_{k}([x_{k-1}, x_{k-2}, ...., x_{0}]) \end{align*} \]

截断补码数值

补码截断也具有相似的属性，只不过要将最高位转换位字符位。

令 \(\vec{x}\) 等于向量 \([x_{\omega-1}, x_{\omega-2}, ...,x_0]\) ，而 \(\vec{x}'\) 是将其截断位 k 位的结果： \(\vec{x}'=[x_{k-1}, x_{k-2}, ..., x_0]\) 。令 \(x=B2U_{\omega}(\vec{x}),x'=B2T_{k}(\vec{x}')\) 。则 \(x'=B2T_{k}(x\ mod\ 2^k)\) 。

2.2.8 关于有符号数与无符号数的建议

有符号数到无符号数的隐式强制类型转换导致了某些非直观的行为。而这些非直观的特性经常导致程序错误，并且这种包含隐式强制类型转换的细微差别的错误很难被发现。

有符号数到无符号数的隐式转换，会导致错误和漏洞。避免这类错误的一种方式是绝不使用无符号数。但是在某些情况下，例如模运算和多精度运算时，无符号值又非常有用。需要程序员根据情况自行决断。

2.3 整数运算

2.3.1 无符号加法

两个非负整数 x 和 y，满足 \(0\leq x, y <2^{\omega}\) 。其和满足 \(0\leq x+y \leq z^{\omega+1}-2\) 。可以看出字长发生“膨胀”，如果我们选择不对字长做任何限制，例如 Lisp 语言，那么就可以得到无限精度的运算结果，但是实际上往往采用固定运算，即其“加法”和“乘法”之类运算不同于它们在整数上的相应运算。

为参数 x 和 y 定义运算 \(+_{\omega}^{u}\) ，其中 \(0\leq x, y<2^{\omega}\) ，其操作是把整数和 x+y 截断为 \(\omega\) 位的结果。将这个结果看做是一个无符号数。对此操作描述为：

原理：无符号数加法

对满足 \(0\leq x, y<2^{\omega}\) 的 x 和 y 有：

\[x+_{\omega}^{u}y= \begin{cases} \\ x+y, &x+y<2^{\omega} &正常 \\ x+y-2^{\omega}, &2^{\omega}\leq x+y<2^{\omega+1} &溢出 \end{cases} \]

推导：

对于 \(x+y<2^{\omega}\) ，和的 \(\omega-1\) 位表示中最高位为 0，无需理会；对于 \(2^{\omega}\leq x+y<2^{\omega+1}\) ，最高位为 1，舍弃最高位相当于从和中减去了 \(2^\omega\) 。

原理：检测无符号数加法中的溢出

对在范围 \(0\leq x, y\leq UMax_{\omega}\) 中的 x 和 y，令 \(s\overset{.}{=}x+_{\omega}^{u}y\) ，对于计算 s，当且仅当 \(s<x\) 或者等价地 \(s<y\) 时，发生了溢出。

推导：

如果发生溢出，那么就有 \(s=x+y-2^{\omega}\) ，假设 \(y<2^{\omega}\) ，就有 \(s=x+(y-2^{\omega})<x\) 。

原理：无符号数求反

对满足 \(0\leq x <2^{\omega}\) 的任意 x, 其 \(\omega\) 位的无符号逆元 \(-_{\omega}^{u}x\) 由下式给出：

\[-_{\omega}^{u}= \begin{cases} x, &x=0 \\ 2^{\omega}-x, &x>0 \end{cases} \]

推导：

对于 \(x>0\) ，观察 \(0<2^{\omega}-x<2^{\omega}\) ，并且 \((x+2^{\omega}-x)\ mod\ 2^{\omega}=0\) 。因此，它就是 x 在 \(+_{\omega}^{u}\) 下的逆元。

2.3.2 补码加法

同理，对给定范围 \(-2^{\omega-1}\leq x, y\leq 2^{\omega-1}-1\) 之内的值，二者和的范围 \(-2^{\omega}\leq x+y \leq 2^{\omega}-2\) 。需要进行截断到 \(\omega\) 位，以避免数据大小的不断扩张。定义 \(x+_{\omega}^{t}y\) 为整数和 \(x+y\) 被截断为 \(\omega\) 位的结果。

原理：补码加法

对满足 \(-2^{\omega-1}\leq x, y\leq 2^{\omega-1}-1\) 的整数 x 和 y，有：

\[x+_{\omega}^{t} y= \begin{cases} x+y-2^{\omega},&2^{\omega-1}\leq x+y &正溢出 \\ x+y, &-2^{\omega-1}\leq x+y <2^{\omega-1} &正常 \\ x+y+2^{\omega}, &x+y<-2^{\omega-1} &负溢出 \end{cases} \]

推导：

我们已知无符号数的加法，那么可以借此求得补码的加法：

\[\begin{align*} x+_{\omega}^{t}y&=U2T_{\omega}(T2U_{\omega}(x)+_{\omega}^{u}T2U_{\omega}(y))\\ &=U2T_{\omega}[(x_{\omega-1}2^{\omega}+x+y_{\omega-1}2^{\omega}+y)]\ mod\ 2^{\omega} \\ &=U2T_{\omega}[(x+y)\ mod\ 2^{\omega}] \end{align*} \]

负溢出得到的结果大于整数之和，正溢出得到的结果小于整数之和。

原理：检测补码加法中的溢出

对满足 \(TMin_{\omega}\leq x, y \leq TMax_{\omega}\) 的 x 和 y，令 \(s\overset{.}{=}x+_{\omega}^{t}y\) 。当且仅当 \(x>0, \ y>0\) ，但 \(s\leq 0\) 时，计算 s 发生了正溢出。当且仅当 \(s<0,\ y<0\) ，但 \(s\geq 0\) 时，计算 s 发生负溢出。

2 .3.3 补码的非

原理：补码的非

对满足 \(TMin_{\omega}\leq x\leq TMax_{\omega}\) 的 x，其补码的非 \(-_{\omega}^{t}x\) 由下式给出

\[-_{\omega}^{t}x= \begin{cases} TMin_{\omega}, &x=TMin_{\omega} \\ -x, &x>TMin_{\omega} \end{cases} \]

推导：

对于 \(TMin_{\omega}+TMin_{\omega}=-2^{\omega-1}+(-2^{\omega-1})=-2^{\omega}\) ，导致负溢出，所以实际上 \(TMin_{\omega}+_{\omega}^{t}TMin_{\omega}=-2^{\omega}+2^{\omega}=0\) ，即满足 \(x>TMin_{\omega}\) 的 x，数值-x 可以表示一个 \(\omega\) 位的补码，对于 \(x=TMin_{\omega}\) 的数则其非是它本身。

补充

计算一个位级表示的值的补码非有几种聪明的方法。

对于任意数值 x，计算表达式 \(-x\) 和 \(\sim x+1\) 得到的结果完全一致。例如：0xa（-6）的补为 -6 （0101->5，5+1 的负数），这在计算较大位表示值时十分有用。例如：0xfffffffa 的补码为-6。

将位向量分为两部分，假设 \(k\) 是最右边的 1 的位置，因而 \(x\) 的位级表示形如 \([x_{\omega-1},x_{\omega-2},...,x_{k+1},1,0,...,0]\) ，这个值的非即为 \([\sim x_{\omega-1},\sim x_{\omega-2},...,\sim x_{k+1},1,0,...,0]\) 。即对位 \(k\) 左边的所有位取反。例如：0x0111（7）的补码非为 0x10h01（-7）；再比如 0x0101（5）的补码非为 0x1011（-5）

2.3.4 无符号乘法

练习题

2.1 完成下面的数字转换：

A. 将 0x39A7F8 转换为二进制。

B. 将二进制 1100100101111011 转换为十六进制。

C. 将 0xD5E4C 转换为二进制。

D. 将二进制 1001101110011110110101 转换为十六进制。

hex:     3    9    A    7    F    8
bin:  0011 1001 1010 0111 1111 1000

bin:  1100 1001 0111 1011
hex:     C    9    7    B

hex:     D    5    E    4    C
bin:  1101 0101 1110 0010 1100

bin:  0010 0110 1110 0111 1011 0101
hex:     2    6    E    7    B    5

2.2 填写下表中的空白项，给出 2 的不同次幂的二进制和十六进制表示：

n	\(2^n\) （十进制）	\(2^n\) （十六进制）
9	512	0x200
19
	16384
		0x10000
17
	32
		0x80

得出结果为：

n	\(2^n\) （十进制）	\(2^n\) （十六进制）
9	512	0x200
19	524288	0x80000
14	16384	0x4000
16	65536	0x10000
17	131072	0x20000
5	32	0x20
7	128	0x80

2.3 一个字节可以用两个十六进制数字来表示。填写下表中缺失的项，给出不同字节模式下的十进制、二进制和十六进制值：

十进制	二进制	十六进制
0	0000 0000	0x00
167	1010 0111	0xA7
62	0011 1110	0x3E
188	1011 1100	0xBC
55	0011 0111	0x37
136	1000 1000	0x88
243	1111 0011	0xF3
82	0101 0010	0x52
172	1010 1100	0xAC
231	1110 0111	0xE7

2.4 不将数字转换为十进制或者二进制，试着解答下面的算术题，答案要用十六进制表示。提示：只要将执行十进制加法和减法所使用的方法改成以16为基数。

A. 0x503c+0x8=

B. 0x503c-0x40=

C. 0x503c+64=

D. 0x50ea-0x503c=

A. 0x503c + 0x8 = 0x5044

B. 0x503c - 0x40 = 0x4ffc

C. 0x503c + 64 (即0x40) = 0x507c

D. 0x50ea - 0x503c = 0xae

2.5 思考下面对 show_bytes 的三次调用：

int val = 0x87654321;
byte_pointer valp = (byte_pointer) &val;
show_bytes(valp, 1); /* A. */
show_bytes(valp, 2); /* B. */
show_bytes(valp, 3); /* C. */

指出在小端法机器和大端法机器上，每次调用的输出值。

需要注意到，show_bytes 中第二参数的数据类型为 size_t，传递的是字节。

A
- 小端法：21
- 大端法：87
B
- 小端法：21 43
- 大端法：87 65
C
- 小端法：21 43 65
- 大端法：87 65 43

2.6 使用show_int和show_float，我们确定整数3510593的十六进制表示为0x00359141，而浮点数3510593.0的十六进制表示为0x4A564504。

A. 写出这两个十六进制值的二进制表示。

B. 移动这两个二进制串的相对位置，使得它们相匹配的位数最多。有多少位相匹配呢？

C. 串中的什么部分不相匹配？

hex:     0    0    3    5    9    1    4    1
bin:  0000 0000 0011 0101 1001 0001 0100 0001

hex:     4    A    5    6    4    5    0    4
bin:  0100 1010 0101 0110 0100 0101 0000 0100

   0    0    3   5   9   1   4   1
0000 0000 001101011001000101000001
             |   	             |
  0100 1010 010101100100010100000100
     4    A    5   6   4   5   0   4

共 21 位与之匹配。

C. 浮点数前九位和后两位不相匹配。发现仅整数的最高位（符号位）没有嵌入在浮点数中。

2.7 下面对 show_bytes 的调用将输出什么结果？

const char* s = "abcdef";
show_bytes((byte_pointer))s, strlen(s));

注意字母‘a’～‘z’的 ASCII 码为 0x61~0x7A

abcdef 的 ASCII 码转换为：0x616263646566。由于 s 字符串长为 7，但是库函数 strlen 不计算终止的空字符，所以输出结果为： abcdef

2.8 填写下表，各出位向量的布尔运算的求值结果。

运算	结果
`a`	[0110 1001]
`b`	[0101 0101]
`~a`
`~b`
`a&b`
`a\|b`
`a^b`
结果为：

运算	结果
`a`	[0110 1001]
`b`	[0101 0101]
`~a`	[1001 0110]
`~b`	[1010 1010]
`a&b`	[0100 0011]
`a\|b`	[0111 1101]
`a^b`	[0011 1100]

2.9 通过混合三种不同颜色的光（红色、绿色和蓝色），计算机可以在视频屏幕或者液晶显示器上产生彩色的画面。设想一种简单的方法，使用三种不同颜色的光，每种光都能打开或关闭，投射到玻璃屏幕上，如图所示：

2.9

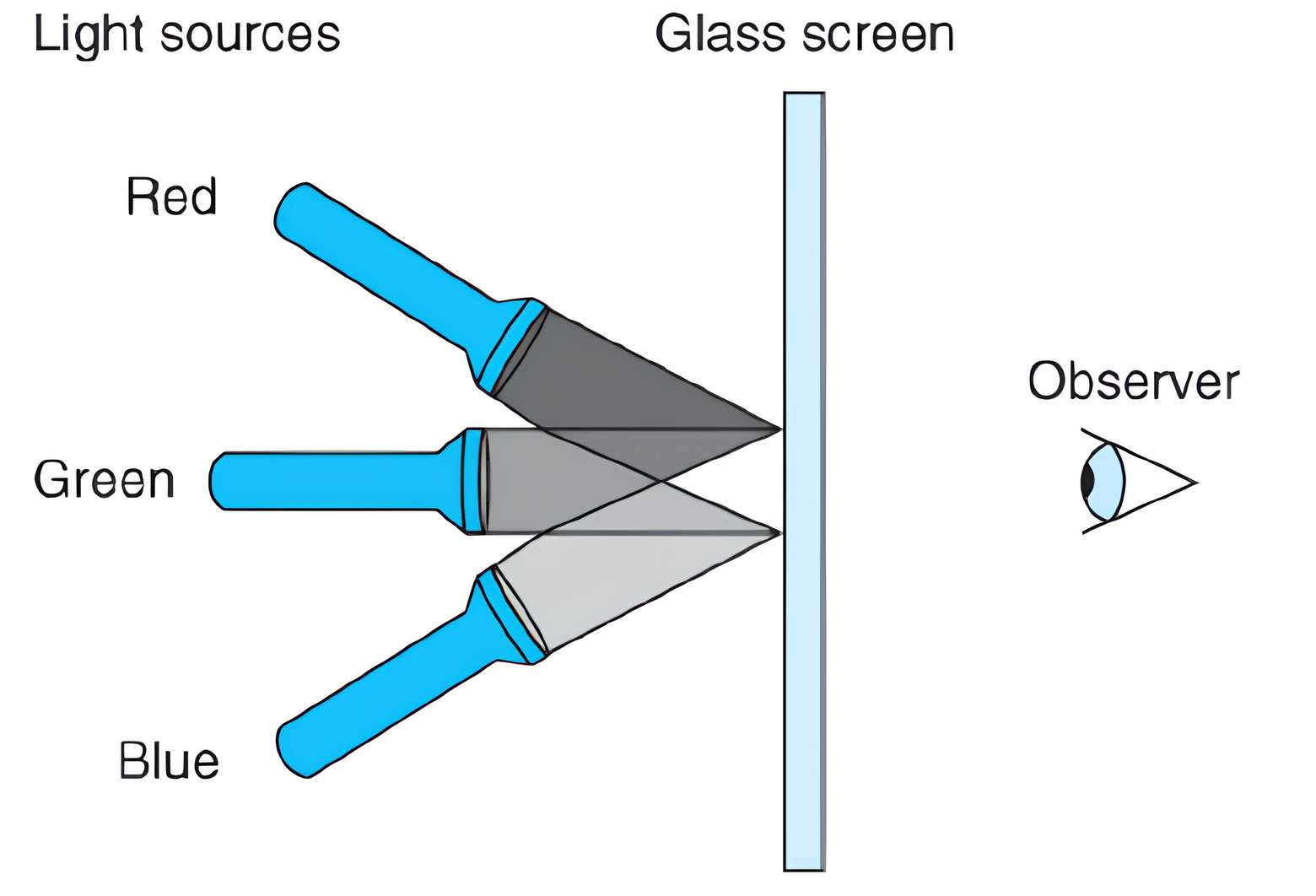
那么基于光源R（红）、G（绿）、B（蓝）的关闭（0）或打开（1），我们就能够创建8种不同的颜色：

R	G	B	颜色
0	0	0	黑色
0	0	1	蓝色
0	1	0	绿色
0	1	1	蓝绿色
1	0	0	红色
1	0	1	红紫色
1	1	0	黄色
1	1	1	白色

这些颜色中的每一种都能用一个长度为3的位向量来表示，我们可以对它们进行布尔运算。

A.一种颜色的补是通过关掉打开的光源，且打开关闭的光源而形成的。那么上面列出的8种颜色每一种的补是什么？

B.描述下列颜色应用布尔运算的结果：
蓝色 | 绿色 =
黄色 & 蓝绿色 =
红色 ^ 红紫色 =

A. 所谓颜色的补就是 \(\sim RGB\) ,可得：

原色	R	G	B	补色
黑色	1	1	1	白色
蓝色	1	1	0	黄色
绿色	1	0	1	红紫色
蓝绿色	1	0	0	红色
红色	0	1	1	蓝绿色
红紫色	0	1	0	绿色
黄色	0	0	1	蓝色
白色	0	0	0	黑色

蓝色 | 绿色 = 001 | 010 = 011，为蓝绿色
黄色 & 蓝绿色 = 110 & 011 = 010，为绿色
红色 ^ 红紫色 = 100 ^ 101 = 001，蓝色

2.10 对于任一位向量 a，有 a^a = 0。应用这一属性，考虑下面的程序：

void inplace_swap(int* x, int* y){
	*y = *x ^ *y; /* Step 1 */
	*x = *x ^ *y; /* Step 2 */
	*y = *x ^ *y; /* Step 3 */
}

正如程序名字所暗示的那样，我们认为这个过程的效果是交换指针变量和所指向的存储位置处存放的值。注意，与通常的交换两个数值的技术不一样，当移动一个值时，我们不需要第三个位置来临时存储另一个值。这种交换方式并没有性能上的优势，它仅仅是一个智力游戏。

以指针 x 和 y 指向的位置存储的值分别是 α 和 b 作为开始，填写下表，给出在程序的每一步之后，存储在这两个位置中的值。利用^的属性证明达到了所希望的效果。回想一下，每个元素就是它自身的加法逆元（a ^ a = 0）。

步骤	*x	*y
初始	`a`	`b`
第 1 步
第 2 步
第 3 步

结果为：

步骤	*x	*y
初始	`a`	`b`
第 1 步	`a`	`a^b`
第 2 步	`b`	`a^b`
第 3 步	`b`	`a`

2.11 在 2.10 中的 inplace_swap 函数的基础上，你决定写一段代码，实现将一个数组中的元素头尾两端依次对调。你写出下面这个函数：

void reverse_array(int a[], int cnt){
	int first, last;
	for(first = 0, last = cnt-1; first <= last; first++, last--)
	    inplace_swap(&a[first], &a[last]);
}

当你对一个包含元素 1、2、3 和 4 的数组使用这个函数时，正如预期的那样，现在数组的元素变成了 4、3、2 和 1 。不过，当你对一个包含元素 1、2、3、4 和 5 的数组使用这个函数时，你会很惊奇地看到得到数字的元素为 5、4、0、2 和 1 。实际上，你会发现这段代码对所有偶数长度的数组都能正确地工作，但是当数组的长度为奇数时，它就会把中间的元素设置成 0。

A.对于一个长度为奇数的数组，长度 cnt=2k十1，函数 reverse_array最后一次循环中，变量 first 和 last 的值分别是什么？

B.为什么这时调用函数 inplace_swap 会将数组元素设置为 0？

C.对 reverse_array 的代码做哪些简单改动就能消除这个问题？

将 for 循环中 first<=last 修改为 first<last ，因为当二者相等时，进行指针地址替换时，根据 a^a=0 得到二者的指针地址都将修改为 0。

2.12 对于下面的值，写出变量 x 的 C 语言表达式。你的代码应该对任何字长 \(\omega \ge 8\) 都能工作。我们给出了当 x=0x87654321 以及 \(\omega\) =32 时表达式求值的结果，仅供参考。

A. x的最低有效字节，其他位均置为0。[0x00000021]

B. 除了 x 的最低有效字节外，其他的位都取补，最低有效字节保持不变。[0x789ABC21]。

C. x的最低有效字节设置成全 1，其他字节都保持不变。［0x876543FF]。

x & 0xFF

x ^ ～ 0xFF

x | 0xFF

2.13 从 20 世纪 70 年代末到 80 年代末，Digital Equipment 的 VAX 计算机是一种非常流行的机型。它没有布尔运算 AND 和 OR 指令，只有 bis (位设置）和 bic (位清除）这两种指令。两种指令的输入都是一个数据字 x 和一个掩码字 m。它们生成一个结果 z，z 是由根据掩码 m 的位来修改 x 的位得到的。使用 bis 指令，这种修改就是在 m 为1的每个位置上，将 z 对应的位设置为 1。使用 bic 指令，这种修改就是在 m 为1的每个位置，将 z 对应的位设置为0。

为了看清楚这些运算与 C 语言位级运算的关系，假设我们有两个函数 bis 和 bic 来实
现位设置和位清除操作。只想用这两个函数，而不使用任何其他 C 语言运算，来实现按位|和~运算。填写下列代码中缺失的代码。提示：写出 bis 和 bic 运算的C语言表达式。

/* Declarations of functions implementing operations bis and bic */
int bis(int x, int m);
int bic(int x, int m);

/* Compute x|y using only calls to functions bis and bic */
int bool_or(int x, int y){
	int result = ____;
	return result;
}

/* Compute x^y using only calls to functions bis and bic */
int bool_xor(int x, int y){
	int result = ____;
	return result;
}

第一个空填写 bis(int x, int y) 。 bis 函数相当于布尔运算 OR。

第二空填写 bis(bic(x,y),bic(y,x)) 。 bic 函数相当于 x&~m ，其利用 x^y=(x&~y)|(~x&y) 的属性。

2.14 假设 x 和 y 的字节值分别为 0x66 和 0x39。填写下表，指明各个 C 表达式的字节值

表达式	值
`x&y`
`x \| y`
`~x \| ~y`
`x & !y`
`x && y`
`!x \|\| !y`
`x && ~y`

将 x 和 y 的值化为二进制值：

hex:     6    6
bin:  0110 0110

hex:     3    9
bin:  0011 1001

易得：

x & y = 0010 0000 = 0x20
x | y = 0111 1111 = 0x7F
~x | ~y = 1101 1111 = 0xDF
x & !y = 0 = 0x00
x && y = 1 = 0x01
x || y = 1 = 0x01
!x || !y = 0 =0x00
x && ~y = 1 = 0x01

2.15 只使用位级和逻辑运算，编写一个 C 表达式，它等价于 x==y。换句话说，当 x 和 y 相等时它将返回 1, 否则就返回 0。

C 表达式可以写为： if(!(x^y)) 。具体运用可查看 exercise_2_15。

2.16 填写下表，展示不同移位运算对单字节数的影响。思考移位运算的最好方式是使用二进制表示。将最初的值转换为二进制，执行移位运算，然后再转换回十六进制。每个答案都应该是8个二进制数字或者2个十六进制数字。

x	x	x<<3	x<<3	x>>2 (逻辑的)	x>>2(逻辑的)	x>>2(算术的)	x>>2 （算术的）
十六进制	二进制	二进制	十六进制	二进制	十六进制	二进制	十六进制
0xC3	1100 0011	0001 1000	0x18	0011 0000	0x30	1111 0000	0xF0
0x75	0111 0101	1010 1000	0xA8	0001 1101	0x1D	0001 1101	0x1D
0x87	1000 0111	0011 1000	0x38	0010 0001	0x21	1110 0001	0xE1
0x66	0110 0110	0100 0000	0x30	0001 1001	0x19	0001 1001	0x19

2.17 假设 \(\omega=4\) ，我们能给每个可能的十六进制数字赋予一个数值，假设用一个无符号或者补码表示。请根据这些表示，通过写出等式 \(B2U_{\omega}(\vec{x})\overset{.}{=}\sum\limits_{i=0}^{\omega-1}x_{i}2^{i}\) 和等式 \(B2T_{\omega}(\vec{x})\overset{.}{=}-x_{\omega-1}2^{\omega-1}+\sum\limits_{i=0}^{\omega-2}x_{i}2^{i}\) 所示的求和公式中的2的非零次幂，填写下表：

\(\vec{x}\) 十六进制	\(\vec{x}\) 二进制	\(B2U_4(\vec{x})\)	\(B2T_4(\vec{x})\)
0xE	[1110]	\(2^3+2^2+2^1=14\)	\(-2^3+2^2+2^1=-2\)
0x0	[0000]	\(0=0\)	\(0=0\)
0x5	[0101]	\(2^2+2^0=5\)	\(2^2+2^0=5\)
0x8	[1000]	\(2^3=8\)	\(-2^3=-8\)
0xD	[1101]	\(2^3+2^2+2^0=13\)	\(-2^3+2^2+2^0=-3\)
0xF	[1111]	\(2^3+2^2+2^1+2^0=15\)	\(-2^3+2^2+2^1+2^0=-1\)

2.18 在第3章中，我们将看到由反汇编器生成的列表，反汇编器是一种将可执行程序文件转换回可读性更好的ASCII码形式的程序。这些文件包含许多十六进制数字，都是用典型的补码形式来表示这些值。能够认识这些数字并理解它们的意义（例如它们是正数还是负数），是一项重要的技巧。

在下面的列表中，对于标号为 A～I（标记在右边）的那些行，将指令名（sub、mov和add）右边显示的（32位补码形式表示的）十六进制值转换为等价的十进制值。

4004d0:    48 81 ec e0 02 00 00     sub    $0x2e0,%rsp             A.
4004d7:    48 8b 44 24 a8           mov    -0x58(%rsp),%rax        B.
4004dc:    48 03 47 28              add    0x28(%rdi),%rax         C.
4004e0:    48 89 44 24 d0           mov    %rax,-0x30(%rsp)        D.
4004e5:    48 8b 44 24 78           mov    0x78(%rsp),%rax         E.
4004ea:    48 89 87 88 00 00 00     mov    %rax,0x88(%rdi)         F.
4004f1:    48 8b 84 24 f8 01 00     mov    0x1f8(%rsp),%rax        G.
4004f8:    00
4004f9:    48 03 44 24 08           add    0x8(%rsp),%rax
4004fe:    48 89 84 24 cO 00 00     mov    %rax,0xc0(%rsp)         H.
400505:    00
400506:    48 8b 44 d4 b8           mov    -0x48(%rsp,%rdx,8),%rax I.

A. 0x2e0=2*16^2+2*16=736
B. -0x58=-88
C. 0x28=40
D. -0x30=48
E. 0x78=120
F. 0x88=136
G. 0x1f8=504
H. 0xc0=176
I. -0x48=72

2.19 利用你解答练习题2.17 时填写的表格，填写下列描述函数 \(T2U_4\) 的表格。

\(x\)	\(T2U_{4}(x)\)
-8	8
-3	13
-2	14
-1	15
0	0
5	5

2.20 请说明等式

\[T2U_{\omega}(x) = \begin{cases} x+2^{\omega}, &x<0 \\ x, &x\geq0 \\ \end{cases} \]

是如何应用到解答练习题2.19时生成的表格中的各项的。

-8=-8+2^4=8
-3=-3+2^4=13
-2=-2+2^4=14
-1=-1+2^4=15
0=0
5=5

2.21 假设在采用补码运算的32位机器上对这些表达式求值，按照下表的格式填写下表，描述强制类型转换和关系运算的结果。

表达式	类型	求值
0 == 0U	无符号	1
-1 < 0	有符号	1
-1 < 0U	无符号	0*
2147483647 > -2147483647-1	有符号	1
2147483647U > -2147483647-1	无符号	0*
2147483647 > (int)2147483648U	有符号	1*
-1 > -2	有符号	1
(unsigned)-1 > -2	无符号	1

表达式	类型	求值
-2147483647-1 == 2147483648U	无符号	0*
-2147483647-1 < 2147483647	有符号	1
-2147483647-1U < 2147483647	无符号	0*
-2147483647-1 < -2147483647	有符号	1*
-2147483647-1U < -2147483647	无符号	0*

2.22 通过应用等式

\[B2T_{\omega}(\vec{x})\overset{.}{=}-x_{\omega-1}2^{\omega-1}+\sum\limits_{i=0}^{\omega-2} X_{i}2^{i} \]

表明下面每个位向量都是-5 的补码表示。
A. [1011]

B. [11011]

C. [111011]

1011=-2^3+2^1+2^0=-5
11011=-2^4+2^3+2^1+2^0=-5
111011=-2^5+2^4+2^3+2^1+2^0=-5

2.23 考虑下面的 C 函数：

int fun1(unsigned word) {
	return (int) ((word << 24) >>> 24);
}

int fun2(unsigned word) {
	return ((int) word << 24) >>24;
}

假设在一个采用补码运算的机器上以32位程序来执行这些函数。还假设有符号数值的右移是算术右移，而无符号数值的右移是逻辑右移。

A.填写下表，说明这些函数对几个示例参数的结果。你会发现用十六进制表示来做会更方便，只要记住十六进制数字8到F的最高有效位等于1。

w	fun1 (w)	fun2 (w)
0x00000076	118
0x87654321
0x000000C9
0xEDCBA987

B. 用语言来描述这些函数执行的有用计算。

通过 exercise_2_23 查看代码运行结果。

w	fun1 (w)	fun2 (w)
0x00000076	118	118
0x87654321	33	33
0x000000C9	201	-55
0xEDCBA987	135	-121

总结：当最高位十六进制值 \(< 8\) ,那么 fun1 和 fun2 函数得到的值相同的，因为二者补码和无符号数都是一致的。但是如果 \(\geq 8\) ，那么 fun1 通过无符号数转换得来，fun2 是通过补码转换而来，要判断最高位是否为 1。

2.24 假设将一个 4 位数值（用十六进制数字 0~F 表示）截断到一个 3 位数值(用十六进制数字 0~7 表示)。填写下表，根据那些位模式的无符号和补码解释，说明这种截断对某些情况的结果。

十六进制	十六进制	无符号	无符号	补码	补码
原始值	截断值	原始值	截断值	原始值	截断值
0	0	0		0
2	2	2		2
9	1	9		-7
B	3	11		-5
F	7	15		-1

解释如何将等式 \(B2U_{k}[x_{k-1}, x_{k-2},..., x_{0}]=B2U_{\omega}([x_{\omega-1}, x_{\omega-2},..., x_{0}])\ mod\ 2^{k}\) 和等式 \(B2T_{k}[x_{k-1},x_{k-2},...,x_{0}]=U2T_{k}(B2U_{\omega}([x_{\omega-1},x_{\omega-2},...,x_{0}])\ mod\ 2^{k})\) 应用到这些示例上。

十六进制	十六进制	无符号	无符号	补码	补码
原始值	截断值	原始值	截断值	原始值	截断值
0	0	0	0	0	0
2	2	2	2	2	2
9	1	9	1	-7	1
B	3	11	3	-5	3
F	7	15	7	-1	-1

截断后，如果是 \(B2U_{k}\) 那么直接得到结果，如果是 \(B2T_{k}\) 则观察最高位是否为 1。

2.25 考虑下列代码，这段代码试图计算数组 a 中所有元素的和，其中元素的数量由参数 length 给出。

/* WARNING: This is buggy code */
float sum_elements(float a[], unsigned length) {
	int i;
	float result=0;
	for (i = 0; i <= length-1; i++)
	    result += a[i];
	return result;
}

当参数 length 等于0时，运行这段代码应该返回0.0。但实际上，运行时会遇到一个内存错误。请解释为什么会发生这样的情况，并且说明如何修改代码。

代码实现 2.25

由于 length 大小定义为 unsigned ，所以当 length==0 时，for 循环语句中 i 小于一个极大值 0xffffffff ,会取到数组外值，发生数组越界现象，称为“缓冲区溢出（Buffer Overflow）”。

解决思路：将 length 的类型改为 int 即可，依据 2.2.8 节建议。

2.26 现在给你一个任务，写一个函数用来判定一个字符串是否比另一个更长。前提是你要用字符串库函数 strlen, 它的声明如下：

/* Prototype for library function strlen */
size_t strlen(const char *s);

最开始你写的函数是这样的：

/* Determine whether string s is longer than string t */
/* WARNING: This function is buggy */
int strlonger(char *s, char *t) {
	return strlen(s) - strlen(t) > 0;
}

当你在一些示例数据上测试这个函数时，一切似乎都是正确的。进一步研究发现在头文件 stdio.h 中数据类型 size_t 是定义成 unsigned int 的。

A.在什么情况下，这个函数会产生不正确的结果？

B.解释为什么会出现这样不正确的结果。

C.说明如何修改这段代码好让它能可靠地工作。

代码实现 2.26

A. 当 s 比 t 短的时候，会返回不正确值 1。

B. 由于 size_t 被定义为 unsigned int 类型，当二者之差为负数时，该值会变为一个很大的数值，且一定大于 0。所以返回值为 1。

C. return strlen(s) > strlen(t)

引用

posted @ 2024-06-05 17:15 木木亚伦阅读(34) 评论(0) 编辑收藏举报

刷新页面返回顶部

亚伦的博客

第2章信息的表示和处理

2.1 信息存储

2.1.1 十六进制表示法

2.1.2 字数据大小

2.1.3 寻址和字节顺序

2.1.4 表示字符串

2.1.5 表示代码

2.1.6 布尔代数简介

2.1.7 C 语言中的位级运算

2.1.8 C 语言中的逻辑运算

2.1.9 C 语言中的移位运算

2.2 整数表示

2.2.1 整型数据类型

2.2.2 无符号数的编码

2.2.3 补码编码

2.2.4 有符号数和无符号数之间的转换

2.2.5 C 语言中的有符号数与无符号数

2.2.6 扩展一个数字的位表示

2.2.7 截断数字

2.2.8 关于有符号数与无符号数的建议

2.3 整数运算

2.3.1 无符号加法

2.3.2 补码加法

2 .3.3 补码的非

2.3.4 无符号乘法

练习题

引用

公告

亚伦的博客

第2章 信息的表示和处理

2.1 信息存储

2.1.1 十六进制表示法

2.1.2 字数据大小

2.1.3 寻址和字节顺序

2.1.4 表示字符串

2.1.5 表示代码

2.1.6 布尔代数简介

2.1.7 C 语言中的位级运算

2.1.8 C 语言中的逻辑运算

2.1.9 C 语言中的移位运算

2.2 整数表示

2.2.1 整型数据类型

2.2.2 无符号数的编码

2.2.3 补码编码

2.2.4 有符号数和无符号数之间的转换

2.2.5 C 语言中的有符号数与无符号数

2.2.6 扩展一个数字的位表示

2.2.7 截断数字

2.2.8 关于有符号数与无符号数的建议

2.3 整数运算

2.3.1 无符号加法

2.3.2 补码加法

2 .3.3 补码的非

2.3.4 无符号乘法

练习题

引用

公告

第2章信息的表示和处理