第二次作业

1.为什么要用函数？

利用函数可以使代码模块化，增强代码的可读性以及提高编码的效率。

以下是用STLsort函数排序

    #include <bits/stdc++.h>
    using namespace std;
    int main()
    {
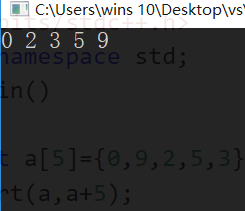
        int a[5]={0,9,2,5,3};
        sort(a,a+5);
    }

2.为什么要用函数重载

利用函数重载可以用同一个函数名实现不同参数的操作，简化编码

以下是用函数重载实现对int和double类型的值相加的功能

    #include <bits/stdc++.h>
    using namespace std;
    int add(int a,int b)
    {
        return a+b;
    }
    double add(double a,double b)
    {
        return a+b;
    }
    int main()
    {
        int a,b;
        double c,d;
        cin>>a>>b>>c>>d;
        add(a,b);
        add(c,d);
        return 0;
    }

3.什么是值传递？

值传递传递的是形参，传递的值的地址与原来的地址不同，对形参的修改不会影响原来的值。

以下是通过传递形参返回两个int类型值中的最大值

    #include <bits/stdc++.h>
    using namespace std;
    int Max(int a,int b)
    {
        return a>b?a:b;
    }
    int main()
    {
        int a,b;
        cin>>a>>b;
        cout<<Max(a,b);
        return 0;
    }

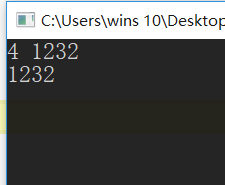
4.什么是地址传递？

地址传递就是通过传递指针的方式，函数的参数变为地址，在函数中的操作可以改变原来的值。

以下是通过传递指针的方式，交换两个int类型的值

    #include <bits/stdc++.h>
    using namespace std;
    void Swap(int *a,int *b)
    {
        int tmp=*a;
        *a=*b;
        *b=tmp;
    }
    int main()
    {
        int a,b;
        cin>>a>>b;
        Swap(&a,&b);
        cout<<a<<' '<<b<<endl;
        return 0;
    }

5.如何编写递归函数？

递归函数有两个要素:出口，子问题。判断一个问题能否用递归解决需要要找出问题是否可以由规模更小的子问题求得和是否存在递归出口(如斐波那契数列)

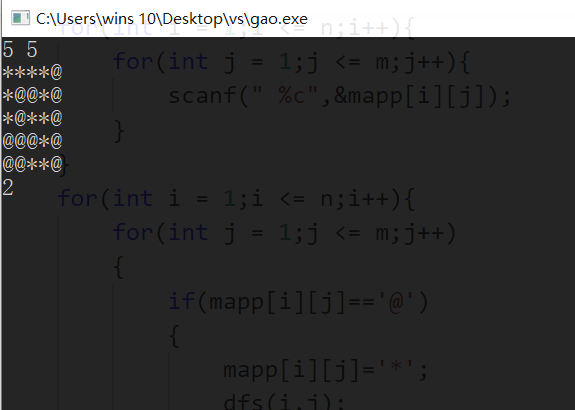
以下是通过递归求图的联通块的个数的代码('@'字符的上下左右，左上，左下，右上，右下存在另一个'@'字符，则这两个字符是联通的)

    #include <iostream>
    #include <cstdio>
    #include <queue>
    #include <stdlib.h>
    #include <cstring>
    using namespace std;
    char mapp[110][110];
    void dfs(int x,int y)
    {
        mapp[x][y]='*';
        int dir[][2]={-1,0,1,0,0,-1,0,1,-1,-1,-1,1,1,1,1,-1};
        for(int i = 0;i < 8;i++)//这里的递归出口就是没有与当前点联通的'@'字符。
        {
            int nx=x,ny=y;
            nx+=dir[i][0];
            ny+=dir[i][1];
            if(mapp[nx][ny]=='@')
                dfs(nx,ny);
        }
    }
    int main()
    {
        int n,m;
        while(~scanf("%d%d",&n,&m)&&m)
        {
            int ans=0;
            for(int i = 1;i <= n;i++){
                for(int j = 1;j <= m;j++){
                    scanf(" %c",&mapp[i][j]);
                }
            }
            for(int i = 1;i <= n;i++){
                for(int j = 1;j <= m;j++)
                {
                    if(mapp[i][j]=='@')
                    {
                        mapp[i][j]='*';
                        dfs(i,j);
                        ans++;
                    }
                }
            }
            printf("%d\n",ans);
        }
        return 0;
    }