跳跃表
常见数据结构的实现【1】:跳跃表
知乎的小伙伴们好,这是我在知乎写的第一篇文章哈。我写这篇文章的目的主要是和大家分享一些想法,交流学习一下。
这系列的文章是分析常见数据结构的实现,包括跳跃表、二叉堆、前缀树、红黑树等等。。。数据结构这门课在学习与工作中都非常重要,所以我觉得有必要把自己的想法拿出来和大家分享交流,互相学习。
下面就开始正题吧!(第一次写文章,如果某些地方语言、思路表达不当或者有误,希望大家包容一下吧哈哈)
介绍
链表是一种基本的数据结构,而跳跃表是一种特殊的有序链表。
- 跳跃表是由多层有序链表组合而成的,最底一层的链表保存了所有的数据,每向上的一层链表依次保存了下一层链表的部分数据。
- 相邻的两层链表中元素相同的节点之间存在引用关系,一般是上层节点中存在一个指向下层节点的引用
- 跳跃表的目的在于提高了查询效率,同时也牺牲了一定的存储空间。
下面的一张图是我自己绘制的跳跃表,每层包含了头节点并且是单向链表:
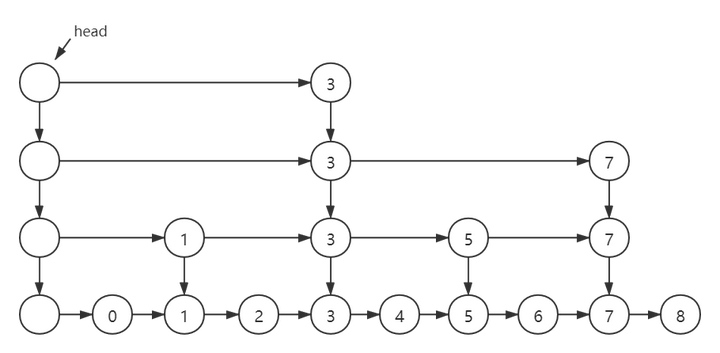
分析
按照上面的图,所有节点包含以下内容:存储的元素,指向同一层中下一个节点的引用,指向下一层中对应节点的引用。
那么我们可以如下构建节点类和跳跃表类:
//跳跃表的实现
//元素有序且不重复
public class SkipList {
private Node head;//顶层头节点
private int rate;//相邻两层元素个数的比例
private int level;//跳跃表层数
private int length;//底层节点个数
private int size;//所有层节点个数
private final boolean order;//true表示正序,false表示逆序
private Random random;//随机数
private Stack<Node> stack;//保存查询时遍历的节点
//节点类
private static class Node {
private Comparable comparable;
private Node right;//同一层的右边节点
private Node down;//下一层的对应节点
public Node(Comparable comparable) {
this.comparable = comparable;
this.right = null;
this.down = null;
}
}
public SkipList(int rate, int level, boolean order) {
this.rate = rate;
this.level = level;
this.length = 0;
this.size = 0;
this.order = order;
this.random = new Random();
this.stack = new Stack<Node>();
this.head = new Node(null);//头节点的值默认为null
Node temp = head;
for (int i = 1; i < level; i++) {
temp.down = new Node(null);
temp = temp.down;
}
}
}表示相邻两层链表的元素数量之比,也就是下一层每添加多少个元素时,就向上一层继续添加一个元素。这个值可以由个人决定
表示有序链表保存元素的顺序,对于整型数据,从前向后,元素从小到大为
,对于字符型数据,从前向后,元素的字典序依次靠后为
,等等
用于添加操作时生成随机数的种子
表示查询操作时保存查询路径上某些节点的栈,
类可以自己实现
类构造方法的最后几句代码表示初始化几个头节点,其中
指向最上层的头节点。我的实现中跳跃表保存的元素不重复,如果想要保存重复的元素,只需要在原来的基础上稍作修改即可
查找元素
添加、删除操作都依赖于查找操作,所以先介绍查找操作
查找操作是自顶向下、从左向右的,也就是先在最上一层链表中从左向右查找,然后依次向下层查找,直到最下一层的某个节点结束。具体的操作依赖于保存元素的顺序,假设保存的是整型数据, 为
,那么元素从前向后依次变大:
- 先在最上一层查找小于所指定元素的最右的节点,将节点入栈,然后转向下一层
- 在当前层继续向后查找满足上述条件的节点,同样将其入栈,向下一层继续查找,直到查找到最下一层满足条件的节点
从上面的分析中可以知道, 中保存的是查找路径中每层最右边的节点,最底层的那个节点除外。
举个例子,在第一张图中,查找元素 时,查找路径为
,
中保存的元素依次为
。查找元素
时,查找路径为
,
中保存的元素依次为
。特殊情况下,头节点也会入栈
为什么这里设计成这样的查找路径,以及栈中保存查找路径上每层最右的节点?主要是在单链表的情况下,查找元素时可以统一元素存在和不存在两种情况,同时添加、删除元素时方便改变节点之间的引用关系。下面贴出查找操作的代码:
//查询元素,自顶向下
//正序时,返回底层【小于】给定值的最大的节点,包含头节点
//逆序时,返回底层【大于】给定值的最小的节点,包含头节点
private Node search(Comparable comparable) {
stack.clear();
Node temp = head;//从顶层开始
while (true) {
while (temp.right != null) {
if (order && temp.right.comparable.compareTo(comparable) >= 0)//正序时查找当前层【小于】给定值的最大的节点
break;
if (!order && temp.right.comparable.compareTo(comparable) <= 0)//逆序时查找当前层【大于】给定值的最小的节点
break;
temp = temp.right;
}
if (temp.down == null)//找到底层的节点
break;
stack.push(temp);//stack保存遍历路径中每一层最右边的节点,除底层外
temp = temp.down;//转到下一层
}
return temp;
}如果理解了查找操作的过程,那么上面的代码就很容易看懂了。查找操作返回的是最下一层满足那个条件的节点(有可能是头节点)。
添加元素
在我的实现中,跳跃表不保存重复的元素,所以只有当所指定元素不存在时,才执行添加操作。
添加操作是自底向上的,并且根据指定的 按照一定的概率向上层添加节点。添加时需要维护同层节点之间的关系,同时也要维护当前节点与下一层对应节点的关系。这里只需要注意的一点是,什么条件下才能向上层继续添加?只有当随机数满足条件并且当前层不是最上一层时,才能继续添加。
//添加元素
//若元素已存在,则返回,保证无重复元素
public void insert(Comparable comparable) {
Node temp = search(comparable);
if (temp.right != null && temp.right.comparable.compareTo(comparable) == 0)//元素已存在
return;
Node node = new Node(comparable);
Node other;
//根据随机数,自底向上添加每层的新节点
while (true) {
node.right = temp.right;
temp.right = node;//当前层添加完毕
size++;
if (random.nextInt(rate) != 0 || stack.isEmpty())
break;
//若随机数为0且还未到顶层,则向上层添加元素
temp = stack.pop();
other = node;
node = new Node(comparable);
node.down = other;
}
length++;
return;
}再强调一下,查找操作返回的是最下一层满足条件的节点。注意下, 循环里面向上层添加单个节点的过程实际上分解到了两次循环中,先维护上下层节点的关系,再维护同层节点的关系。
删除元素
当所指定元素存在时,删除操作需要删除所有层中的对应元素。如果某一层中不存在指定的元素,那么上面的所有层中肯定也不会存在,因此可以直接跳出循环,操作结束。
//删除元素
//若元素不存在,则返回,否则删除所有层中包含的元素
public void delete(Comparable comparable) {
Node temp = search(comparable);
if (temp.right == null || temp.right.comparable.compareTo(comparable) != 0)//元素不存在
return;
while (true) {
if (temp.right == null || temp.right.comparable.compareTo(comparable) != 0) //当前层的元素不存在
break;
//从底层开始,依次删除每层的元素
temp.right = temp.right.right;
size--;
if (stack.isEmpty())//到达顶层
break;
temp = stack.pop();//转到上一层
}
length--;
return;
}后记
从上面的讨论中可以看到,跳跃表的查找、添加、删除操作其实并不难理解,这个数据结构比较简单。当然这篇文章是我的个人理解,欢迎感兴趣的读者一起来交流,提出建议。后面我会介绍其他一些常用数据结构的实现,希望大家继续关注哦~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号