二叉树,红黑树,B+树
在实际使用时会根据链表和有序数组等数据结构的不同优势进行选择。有序数组的优势在于二分查找,链表的优势在于数据项的插入和数据项的删除。但是在有序数组中插入数据就会很慢,同样在链表中查找数据项效率就很低。综合以上情况,二叉树可以利用链表和有序数组的优势,同时可以合并有序数组和链表的优势,二叉树也是一种常用的数据结构。
有序二叉树天然具有对数查找效率;二叉树天然具有链表特征。
与哈希表比较具有天然排序优势。
Oracle索引是B- 树 Mysql是B+树
什么是B树(B-树)?
写在开头:B-树,就是B树。因B树的英文名称为B-tree ,B-树因此而来,有人会误以为B-树是一种树,而B树又是另外一种树。实际上,B-tree就是指的B树。
而且B-树不可以读成B减树。。。
一:预备知识:
磁盘I/O:是指磁盘的输入和输出(Input和Output的缩写)。
二叉查找树(Binary Sort Tree),简称BST,其查找的时间复杂度O(log2N)与树的深度相关,那么降低树的深度自然会提高查找效率。数据库索引一般使用B树存储,其索引存在磁盘中,利用索引查询时,对于数据量大的索引不可能一次全部加载,只是一次次加载磁盘页,在B树中,每个节点的大小为一个磁盘的页。在大量数据中实现索引查询时 ,树节点存储的元素数量是十分有限的,如果元素数量非常多的话,查找就退化成节点内部的线性查找了,二叉查找树结构会因树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下,磁盘查找存取的次数往往由树的高度所决定,为了减少树的深度 我们采用多叉树结构
我们通过 减少树的结构尽量减少树的高度, 减少磁盘查找存取的次数 我们就想到了多路查找树。 许多数据库系统都一般使用B树或者B树的各种变形结构。一棵含n个结点的B树的高度为O(lgn)。
B 树又叫平衡多路查找树。它的每一个节点最多包含k个孩子,k便称为B树的阶。k的大小取决于磁盘页的大小。
1.树中每个结点含有最多含有k个孩子,即k满足:ceil(k/2)<=k<=k (ceil(x)是一个取上限的函数);
2.除根结点和叶子结点外,其它每个结点至少有[ceil(m / 2)]个孩子
3..根节点至少有两个孩子
4..所有叶子结点都出现在同一层
5..每个节点中元素从小到大排列
6..中间的节点有k-1个元素和k个孩子
当单一节点元素很多时,B树在查询时次数不比二叉查找树小,
二:插入:
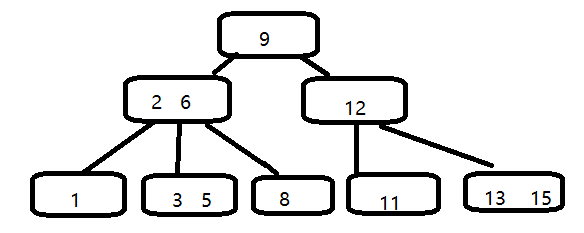
若要插入4,,自顶向下查找4的节点位置,4应该插在3,5之间,2,6和3,5都是两元素节点,无法增加根节点可以升级为两元素结点,4,9.
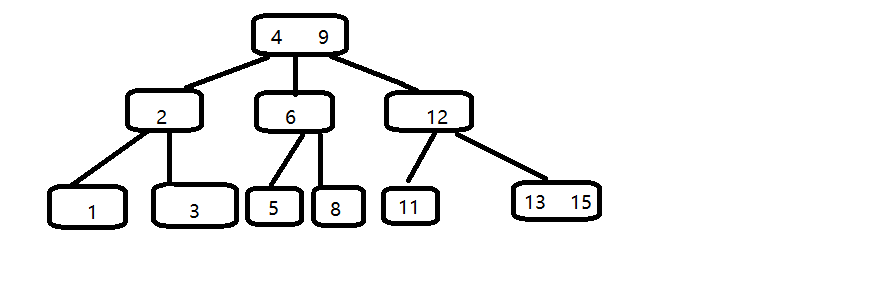
以下节点为符合规则也要改变,维持多路平衡。
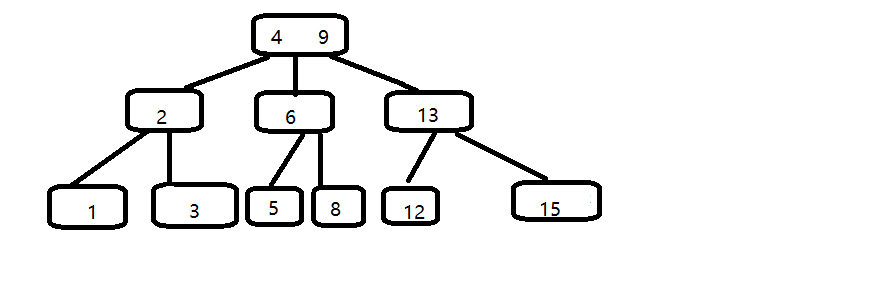
三:删除

例如,我们要删除11,但是12不可只有一个孩子,我们找出12,13,15中的中位数13作为父节点,12下移成为左孩子。
四:应用:
用于部分数据库索引,文件系统等
2.B+树
B+树是对B树的一种变形树,它与B树的差异在于:
- 有k个子结点的结点必然有k个关键码。
- 非叶结点仅具有索引作用,跟记录有关的信息均存放在叶结点中。
-
树的所有叶结点构成一个有序链表,可以按照关键码排序的次序遍历全部记录。
如下图是一个B+树:
 M=4的B+树
M=4的B+树
下图是B+树的建立过程:
 Bplustreebuild.gif
Bplustreebuild.gif
B+树和B树的区别
B+树的非叶子结点只包含导航信息,不包含实际的值,所有的叶子结点和相连的节点使用链表相连,便于区间查找和遍历。
B+ 树的优点在于:
- IO次数更少:由于B+树在内部节点上不包含数据信息,因此在内存页中能够存放更多的key,也就是能存更多的索引。 数据存放的更加紧密,具有更好的空间局部性。因此访问叶子节点上关联的数据也具有更好的缓存命中率。
- 遍历更加方便:B+树的叶子结点都是相链的,因此对整棵树的遍历只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连,所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻,所以缓存命中性没有B+树好。
但是B树也有优点,其优点在于,由于B树的每一个节点都包含key和value,因此经常访问的元素可能离根节点更近,因此访问也更迅速。下面是B 树和B+树的区别图:

为什么MySQL选择B+树做索引
1、 B+树的磁盘读写代价更低:B+树的内部节点并没有指向关键字具体信息的指针,因此其内部节点相对B树更小,也就是能存更多的索引,如果把所有同一内部节点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多,一次性读入内存的需要查找的关键字也就越多,相对IO读写次数就降低了。
2、B+树的查询效率更加稳定:由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
3、B+树更便于遍历:由于B+树的数据都存储在叶子结点中,分支结点均为索引,方便扫库,只需要扫一遍叶子结点即可,但是B树因为其分支结点同样存储着数据,我们要找到具体的数据,需要进行一次中序遍历按序来扫,所以B+树更加适合在区间查询的情况,所以通常B+树用于数据库索引。
4、B+树更适合基于范围的查询:B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题,正是为了解决这个问题,B+树应用而生。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作或者说效率太低。
参考
作者:Jarkata
链接:https://www.jianshu.com/p/7ce804f97967
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
今天看了STL源码剖析中关于红黑树的原理和实现,看完复杂的节点插入、节点颜色变换后不禁想:这些功能经典的AVL树也能实现,为什么要提出红黑树?查了些资料,并且加上自己理解,感叹红黑树的巧妙。
首先红黑树是不符合AVL树的平衡条件的,即每个节点的左子树和右子树的高度最多差1的二叉查找树。但是提出了为节点增加颜色,红黑是用非严格的平衡来换取增删节点时候旋转次数的降低,任何不平衡都会在三次旋转之内解决,而AVL是严格平衡树,因此在增加或者删除节点的时候,根据不同情况,旋转的次数比红黑树要多。所以红黑树的插入效率更高!!!
这里引用一下知乎上的回答:
Answer 1:
1. 如果插入一个node引起了树的不平衡,AVL和RB-Tree都是最多只需要2次旋转操作,即两者都是O(1);但是在删除node引起树的不平衡时,最坏情况下,AVL需要维护从被删node到root这条路径上所有node的平衡性,因此需要旋转的量级O(logN),而RB-Tree最多只需3次旋转,只需要O(1)的复杂度。
2. 其次,AVL的结构相较RB-Tree来说更为平衡,在插入和删除node更容易引起Tree的unbalance,因此在大量数据需要插入或者删除时,AVL需要rebalance的频率会更高。因此,RB-Tree在需要大量插入和删除node的场景下,效率更高。自然,由于AVL高度平衡,因此AVL的search效率更高。
3. map的实现只是折衷了两者在search、insert以及delete下的效率。总体来说,RB-tree的统计性能是高于AVL的。
作者:Acjx
链接:http://www.zhihu.com/question/20545708/answer/58717264
Answer 2 这个总结比较好:
红黑树的 查询性能略微逊色于AVL树,因为他比avl树会稍微不平衡最多一层,也就是说红黑树的查询性能只比相同内容的avl树最多多一次比较,但是,红黑树在插入和删除上完爆avl树, avl树每次插入删除会进行大量的平衡度计算,而红黑树为了维持红黑性质所做的红黑变换和旋转的开销,相较于avl树为了维持平衡的 开销要小得多
作者:陈智超
链接:http://www.zhihu.com/question/43744788/answer/98258881
Answer 3 :
功能、性能、空间开销的折中结果。
AVL更平衡,结构上更加直观,时间效能针对读取而言更高;维护稍慢,空间开销较大。
红黑树,读取略逊于AVL,维护强于AVL,空间开销与AVL类似,内容极多时略优于AVL,维护优于AVL。
基本上主要的几种平衡树看来,红黑树有着良好的稳定性和完整的功能,性能表现也很不错,综合实力强,在诸如STL的场景中需要稳定表现。
作者:Coldwings
链接:http://www.zhihu.com/question/20545708/answer/44370878
所以简单说,如果你的应用中,搜索的次数远远大于插入和删除,那么选择AVL,如果搜索,插入删除次数几乎差不多,应该选择RB。
下面的文章来源:http://blog.csdn.net/klarclm/article/details/7780319
1 好处 及 用途
红黑树并不追求“完全平衡”——它只要求部分地达到平衡要求,降低了对旋转的要求,从而提高了性能。
红黑树能够以O(log2 n) 的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。当然,还有一些更好的,但实现起来更复杂的数据结构 能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高。
当然,红黑树并不适应所有应用树的领域。如果数据基本上是静态的,那么让他们待在他们能够插入,并且不影响平衡的地方会具有更好的性能。如果数据完全是静态的,例如,做一个哈希表,性能可能会更好一些。
在实际的系统中,例如,需要使用动态规则的防火墙系统,使用红黑树而不是散列表被实践证明具有更好的伸缩性。
典型的用途是实现关联数组
2 AVL树是最先发明的自平衡二叉查 找树。在AVL树中任何节点的两个儿子子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis,他们在 1962 年的论文 "An algorithm for the organization of information" 中发表了它。
引入二叉树的目的是为了提高二叉树的搜索的效率,减少树的平均搜索长度.为此,就必须每向二叉树插入一个结点时调整树的结构,使得二叉树搜索保持平衡,从而可能降低树的高度,减少的平均树的搜索长度.
AVL树的定义:
一棵AVL树满足以下的条件:
1>它的左子树和右子树都是AVL树
2>左子树和右子树的高度差不能超过1
从条件1可能看出是个递归定义,如GNU一样.
性质:
1>一棵n个结点的AVL树的其高度保持在0(log2(n)),不会超过3/2log2(n+1)
2>一棵n个结点的AVL树的平均搜索长度保持在0(log2(n)).
3>一棵n个结点的AVL树删除一个结点做平衡化旋转所需要的时间为0(log2(n)).
从1这点来看红黑树是牺牲了严格的高度平衡的优越条件为 代价红黑树能够以O(log2 n)的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。当然,还有一些更好的,但实现起来更复杂的数据结构 能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高.
————————————————
版权声明:本文为CSDN博主「mmshixing」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/mmshixing/article/details/51692892


 浙公网安备 33010602011771号
浙公网安备 33010602011771号