代码随想录刷题笔记

代码随想录刷题

数组

二分查找

• 思路： 有序数组，数组中无重复元素

移除元素

• 思路： 数组在内存地址中是连续的，不能单独删除某个数组中的某个元素，只能覆盖

  • 快慢指针法，用于数组、链表、字符串等的操作

  • 双向指针法，更优，移动更少的元素

• 注意：

  • 补充快慢指针法的代码

  • 交换时候注意只有在交换的时候，左右数组的下标才额外在交换之后移动一位，用left--和right++

有序数组的平方

• 思路： 复数有可能成为最大值，左右比较，放到一个新的数组里面

  • 双向指针法：时间复杂度为o(n)
  • sort的时间复杂度为o(nlogn)

• 注意： 这个里面先求出大的数，因此想得到递增序列之只能从后往前存储。

长度最小的子数组

• 思路： 暴力算法时间复杂度十分高，会超时
  考虑用更优的算法

  • 暴力解法：如果用暴力解法，两个for循环，时间复杂度为o(n^2)

  • 滑动窗口解法：设置一个窗口，不断的移动头和尾，很类似于双指针法

    每一个元素都被操作了两次，是o(n)级别的算法

• 注意：

  • 设置最开始的窗口值要设置成最大的数，防止出现第一次的窗口值很大，小于返回值的初始值，导致无法更新返回值的情况
  • INT32_MAX是c++中定义的宏常量，代表int类型32位整数的最大值

• 代码：

  class Solution {
  public:
  	int minSubArrayLen(int target, vector<int>& nums) {
  		//初始化滑动窗口的大小尾0
  		//INT32_MAX是c++标准库中定义的一个宏函数，代表32位有符号整数的最大值
  		//这里把窗口值的初始值设置为最大
  		//防止第一次出现的窗口过于大，导致第一次窗口的值无法赋给返回值的情况
  		int min_sub_array_len = INT32_MAX;
  		int left = 0;
  		//初始化sum的值
  		int sum = 0;
  		
  		//循环遍历找大于target的窗口
  		for (int i = 0; i < nums.size(); i++) {
  			sum += nums[i];
  			while (sum >= target) {
  				//更新最小窗口值
  				min_sub_array_len = (min_sub_array_len < (i - left + 1)) ? min_sub_array_len : (i - left + 1);
  				//将窗口左边右移,并且将左值减去
  				sum -= nums[left++];
  			}
  		}
  		return min_sub_array_len == INT32_MAX ? 0 : min_sub_array_len;
  	}
  };
  

螺旋矩阵

• 思路： 坚持循环不变量原则

• 注意： 考察对代码的控制

• 代码：

  class Solution {
  public:
  	vector<vector<int>> generateMatrix(int n) {
  		//二维数组中螺旋矩阵，遵循循环不变量原则
  		//都左闭右开，1-n^2，总共有n行n列
  		vector<vector<int>> res(n, vector<int>(n, 0));
  		//总共要转n/2圈
  		int loop = n / 2;
  		//定义每次打印的初始边界
  		int starx = 0, stary = 0;
  		//填充的元素
  		int count = 1;
  		//右边界，每次循环有边界收缩一位
  		int offset = n;
  		//总共转loop圈
  		while (loop--) {
  			int i = starx;
  			int j = stary;
  			//填充从左到右
  			//左闭右开，右边最后一个元素不填充
  			for (j = stary; j < offset - 1; j++) {
  				res[i][j] = count;
  				count++;
  			}
  			//填充从上到下
  			for (i = starx; i < offset - 1; i++) {
  				res[i][j] = count;
  				count++;
  			}
  			//填充从右到左
  			for (; j > starx; j--) {
  				res[i][j] = count;
  				count++;
  			}
  			//填充从下到上
  			for (; i > stary; i--) {
  				res[i][j] = count;
  				count++;
  			}
  			//第二圈的时候，起始位置++
  			starx++;
  			stary++;
  			//收缩右边的值
  			offset--;
  		}
  		//当n为奇数的时候,单独填充中间的元素
  		if (n % 2 != 0) {
  			res[n / 2][n / 2] = count;
  		}
  		return res;
  	}
  };
  

• 总结：

  • 数组中的元素是不能删除的，只能覆盖

  • vector 和 array的区别：

    vector的底层实现是array，vector严格上说只是容器，不是数组

数组的经典算法

• 二分法

  注意界限的控制

  注意循环不变量原则

  看left==right的时候有没有定义成不成立

  时间复杂度是O(logn)

  暴力解决的时间复杂度是O(n)

• 双指针法

  快慢指针法

  时间复杂度是O(n)

  暴力解决的时间复杂度是O(n^2)

• 滑动窗口

  一种特殊的双指针法

  时间复杂度为O(n)

  暴力解决的时间复杂度是O(n^2)

• 模拟行为

  注意循环不变量原则
  主要考察对代码的控制力

链表

移除链表元素

• 代码：

  struct ListNode {
  	int val;
  	ListNode* next;
  	//三个构造函数
  	ListNode() : val(0), next(nullptr) {}
  	ListNode(int x) : val(x), next(nullptr) {}
  	ListNode(int x, ListNode* next) : val(x), next(next) {}
  };
  
  class Solution {
  public:
  	ListNode* removeElements(ListNode* head, int val) {
  		//如果头节点的值等于val
  		//删除头节点
  		while (head != NULL && head->val == val) {
  			ListNode* temp = head;
  			head = head->next;
  			//delete用于释放内存
  			delete temp;
  		}
  		//删除非头节点
  		ListNode* curr = head;
  		//检查的是curr的下一个是不是val
  		while (curr != NULL && curr->next != NULL) {
  			if (curr->next->val == val) {
  				ListNode* temp = curr->next;
  				curr->next = curr->next->next;
  				delete temp;
  			}
  			else {
  				curr = curr->next;
  			}
  		}
  		return head;
  	}
  };
  

设计链表

• 思路： 两种方法

  • 带头节点
  • 不带头节点：实际上应用中都没有头节点

翻转链表

• 思路： 不需要额外空间，直接定义指针

class Solution {
public:
	ListNode* reverseList(ListNode* head) {
		//翻转链表
		//保存curr下一个结点
		ListNode* temp;
		ListNode* curr = head;
		ListNode* pre = NULL;
		
		//当temp不等于NULL的时候
		while (curr){
			temp = curr->next;
			curr->next = pre;
			pre = curr;
			curr = temp;
		}
		return pre;
	}
};

两两交换链表中的节点

• 思路： 如果没有虚拟头结点，第一次对于头节点的处理会比较困难

class Solution {
public:
	ListNode* swapPairs(ListNode* head) {
		//设置一个虚拟头节点
		//设置虚拟头节点和头指针有什么区别？
		//如果设置头节点指针，仍然第一个要对头节点进行操作
		//操作不统一
		ListNode* dummyhead = new ListNode(0);
		dummyhead->next = head;

		//操作要从虚拟节点开始
		ListNode* curr = dummyhead;
		ListNode* temp1 = NULL;
		ListNode* temp2 = NULL;
		while (curr->next != NULL && curr->next->next != NULL) {
			temp1 = curr->next;
			temp2 = curr->next->next->next;

			curr->next = curr->next->next;
			curr->next->next = temp1;
			temp1->next = temp2;
			curr = temp1;
		}
		return dummyhead->next;
	}
};

删除链表的倒数第N个结点

• 思路： 利用快慢指针，让fast指针先走n步，等fast指针指向末尾的时候，slow就指向了倒数第n个结点，要存储slow的pre结点
• 注意： 这个题目在Leecode中free结点编译不通过

class Solution {
public:
	ListNode* removeNthFromEnd(ListNode* head, int n) {
		ListNode* dummynode = new ListNode(0);
		dummynode->next = head;
		ListNode* fast = dummynode, * slow = dummynode;

		//让fast先走n+1步
		for (int i = 0; i < n+1; i++) {
			if (fast == NULL) {
				return dummynode->next;
			}
			fast = fast->next;
		}

		//当fast到末尾的时候。slow指针指向了倒数第n-1个结点
		while (fast) {
			fast = fast->next;
			slow = slow->next;
		}
		//slow结点现在指向了删除节点的上一个结点

		//ListNode* temp;
		//temp = slow->next;
		slow->next = slow->next->next;
		//free(temp);
		return dummynode->next;
	}
};

链表相交

• 思路： 遍历求出两个链表的长度，然后从后往前比较结点的地址是不是相同的

• 注意：

  • 注意应该是地址相同，而不是内容相同。
  • 链表只能单向移动，无法从后往前移动
  • 写代码要细心，不要总是丢失条件

class Solution {
public:

	ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
		int lenA = 0;
		int lenB = 0;
		ListNode* currA = headA;
		ListNode* currB = headB;
		while (currA != NULL)
		{
			lenA++;
			currA = currA->next;
		}
		while (currB != NULL)
		{
			lenB++;
			currB = currB->next;
		}
		//此时currA和currB链表指针都在末尾
		//现在知道了链表的长度
		//让长链表先走差值步
		//直接设置，lenA指向长指针
		currA = headA;
		currB = headB;

		if (lenA < lenB) {
			swap(lenA,lenB);
			swap(currA,currB);
		}

		//长指针先走n步
		int gap = lenA - lenB;
		while (gap--) {
			currA = currA->next;
		}

		//此时让两个指针一起行动，直到相等
		while (currA!=NULL)
		{
			if (currA == currB) {
				return currA;
			}
			currA = currA->next;
			currB = currB->next;
		}
		return NULL;
	}
};

环形链表II

• 思路：
  • 快慢指针，先判断是不是有环
  • 如果有环的话，计算环的大小
  • 快慢指针回到原点，快指针先走环的大小
    • 快慢指针同时走
    • 相遇的地方就是环的入口

class Solution {
public:
	ListNode* detectCycle(ListNode* head) {
		ListNode* fast = head;
		ListNode* slow = head;
		int circle_size = 0;

		//判断是不是有环
		while (fast != NULL && fast->next != NULL) {
			fast = fast->next->next;
			slow = slow->next;
			if (fast == slow) {
				//证明有环
				//计算环的大小
				slow = slow->next;
				circle_size++;
				while (fast != slow) {
					slow = slow->next;
					circle_size++;
				}
				//再次跳进时候已经计算得到了circle_size
				//将fast向前走circle_size距离
				fast = head;
				slow = head;
				while (circle_size--)
				{
					fast = fast->next;
				}
				while (fast != slow)
				{
					fast = fast->next;
					slow = slow->next;
				}
				//再次跳出是相遇在结点
				return fast;
			}
		}
		return NULL;
	}
};

链表经典题目

• 虚拟头节点

  一些头节点需要单独判断是不是为空的操作

• 反转链表

  递归和迭代，设置头节点会简单很多

• 删除倒数第N个节点

• 链表相交

• 环形链表

哈希表

哈希表理论基础

• 哈希函数就是一种数组的映射

• 可以用来快速的判断一个元素是否出现集合里

  数组查询的时间复杂度为O(n)

  哈希表查询的时间复杂读为O(1)，以空间换时间

• 哈希碰撞

  解决哈希碰撞的两种方法

  拉链法：链表

  线性探测法：talesize大于datesize，不然就没有位置去存放冲突的数据了

• 常见的三种哈希结构

  数组

  set（集合）

  map（映射）

  

  

有效的字母异位词

• 思路：
  暴力解法：两层for循环

  哈希表：空间为O(n)，时间复杂度为O(1)

• 注意： 利用ASCII值进行计算

• 代码：

  class Solution {
  public:
  	bool isAnagram(string s, string t) {
  		//申请一个大小为26的数组
  		int arr[26] = { 0 };
  
  		//这个大小位26的数组初始值为0
  		//遍历s，将其映射到数组中
  		for (int i = 0; i < s.size(); i++) {
  			arr[s[i] - 'a']++;
  		}
  		for (int i = 0; i < t.size(); i++) {
  			arr[t[i] - 'a']--;
  		}
  		for (int i = 0; i < 26; i++) {
  			if (arr[i] != 0) {
  				return false;
  			}
  		}
  		return true;
  	}
  };
  

两个数组的交集

• 思路：利用unorder_set，底层实现是哈希表，无序，key无序，key值不可重复，查询效率为O(1)

• 注意：利用数组做哈希表的，都是有大小的数，无大小的数用来做哈希表，容易造成空间的浪费。

• 代码：

  class Solution {
  public:
  	vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
  		//用unorder_set数据结构
  		//存放结果，用哈希set主要是为了给结果去重
  		unordered_set<int> result_set;
  		//括号里加入的是插入nums_set数组的范围
  		unordered_set<int> nums_set(nums1.begin(), nums1.end());
  
  		//循环遍历nums2
  		for (int num : nums2) {
  			//可以理解为尾部的指针，如果找不到num就返回一个尾部的指针
  			if (nums_set.find(num) != nums_set.end()) {
  				result_set.insert(num);
  			}
  		}
  		//是一个函数，相当于把result_set的值复制到一个新的数组中
  		//这里复制到一个新的数组中是应为函数返回值类型为vector<int>
  		return vector<int>(result_set.begin(), result_set.end());
  	}
  };
  

快乐数

• 思路：

  如果sum值重复出现，那就进入无限循环了

  否则就一计算，计算到sum=1为止

  如果不适用哈希表，每次都进行查找，那么时间复杂度会为n^2

• 注意：

• 代码：

  class Solution {
  public:
  	int getSum(int n) {
  		int sum = 0;
  		//当n不等于0的时候
  		while (n)
  		{
  			sum += (n % 10) * (n % 10);
  			n = n / 10;
  		}
  		return sum;
  	}
  
  	bool isHappy(int n) {
  		//定义了一个sum_set数组
  		unordered_set<int> sum_set;
  		//循环运行
  		while (1) {
  			int sum = getSum(n);
  			//是快乐数的返回值
  			if (sum == 1) {
  				return true;
  			}
  			//跳出循环的条件
  			if (sum_set.find(sum) != sum_set.end()) {
  				return false;
  			}
  			else {
  				//插入sum值
  				sum_set.insert(sum);
  			}
  			n = sum;
  		}
  	}
  };
  

两数之和

• 思路：

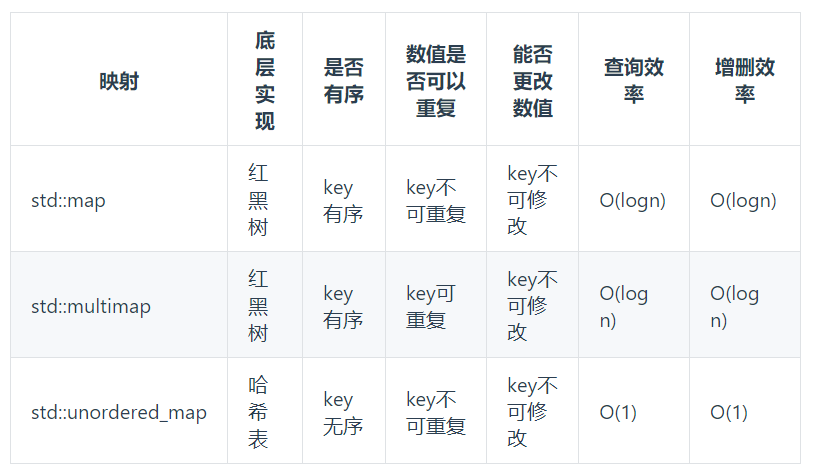
  数组、set、map这三种哈希表的结构中，只有map是key，value对应的

  数组、set、map这三种哈希表的结构都有三种底部实现

  底层实现是红黑树的都是要求key有序

  底层实现是哈希表的查询效率和增删效率都最高，但是是无序实现

• 注意：

• 代码：

  class Solution {
  public:
  	vector<int> twoSum(vector<int>& nums, int target) {
  		//定义一个map数组
  		unordered_map<int,int> map;
  		//遍历数组，在已经访问过的map中寻找是不是有target-nums[i]的数组
  		for (int i = 0; i < nums.size(); i++) {
  			auto iter = map.find(target - nums[i]);
  			if (iter != map.end()) {
  				return { iter->second,i };
  			}
  			//没找到就把数值插入进map中
  			//其中pair<int,int>代表插入一个有序的键值对，模板参数
  			map.insert(pair<int,int>(nums[i], i));
  		}
  		//都没找到返回一个空数组
  		return {};
  	}
  };
  

四数相加

• 思路：

  四个独立的数组，不用考虑有重复的四个元素相加的情况

  和计算两数之和一样，先将一个和存放到数组中，然后对比target-和

• 注意：

  此题不用考虑不许重复出现

  这个题中的unorder_map的用法同上一问不同

• 代码：

  class Solution {
  public:
  	int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
  		//定义一个哈希map
  		unordered_map<int, int> map;
  		int size = nums1.size();
  		//循环遍历插入map
  		//map中的key为和，value为出现的次数
  		for (int a : nums1) {
  			for (int b : nums2) {
  				map[a + b]++;
  			}
  		}
  
  		int count = 0;
  
  		//这个时候map里面就存着两数之和了
  		for (int c : nums3) {
  			for (int d : nums4) {
  				if (map.find(0 - (c + d)) != map.end()) {
  					//找到了累加
  					//这个时候map里面就代表着key，数组的值就代表着value
  					count += map[0 - (c + d)];
  				}
  			}
  		}
  		return count;
  	}
  };
  

赎金信

• 思路：

  暴力枚举：两层for循环

  哈希解法：如果用map的话，底层实现是红黑树和哈希表，map消耗的空间比较大

  ​ 因此用数组更加直接

• 注意：

• 代码：

  class Solution {
  public:
  	bool canConstruct(string ransomNote, string magazine) {
  		//ransomNote中的字母要在magzine中出现
  		int map[26] = {0};
  		for (int i = 0; i < magazine.size(); i++)
  		{
  			//将字符减a作为下标
  			int idex = magazine[i] - 'a';
  			map[idex]++;
  		}
  		//遍历递减，如果出现负数，跳出
  		for (int i = 0; i < ransomNote.size(); i++) {
  			int idex = ransomNote[i] - 'a';
  			map[idex]--;
  			if (map[idex] < 0) {
  				return false;
  			}
  		}
  		return true;
  	}
  };
  

三数之和

• 思路：

  • 哈希法：(思路)

    不好去重，用哈希法来确定a-b的值

    时间复杂度是O(n^2)

    哈希表的额外空间复杂度是O(n)

  • 双指针法

    时间复杂度O(n^2)

    空间复杂度O(1)

• 注意：

  • 去重的逻辑思考，剪枝操作

  • 总共有一轮剪枝

    两轮去重

    第一轮去重是控制第一个元素不要重复

    第二轮去重是控制剩下两个元素不要重复

• 代码：

  class Solution {
  public:
  	vector<vector<int>> threeSum(vector<int>& nums) {
  		//定义一个返回的数组值
  		vector<vector<int>> result;
  
  		//首先对数组进行排序
  		sort(nums.begin(), nums.end());
  
  		//进行循环
  		for (int i = 0; i < nums.size(); i++) {
  			//第一轮剪枝，如果第一个数值大于零，则不存在三数之和为0的情况
  			if (nums[i] > 0) {
  				return result;
  			}
  
  			//第一轮去重，结果的一元数组不可以相同，但是一元数组内的元素可以相同
  			//如果当前位置和下一个位置进行比对，会出现，-1,-1,2
  			//因此去重操作应该是当前位置和前面的元素进行比较
  			if (i > 0 && nums[i] == nums[i - 1]) {
  				continue;
  			}
  			//每一轮开始遍历
  			int left = i + 1;
  			int right = nums.size() - 1;
  
  			//只要遍历基点n的值确定不重复，那就可以确定不重复
  			//基点右边是一个二分查找
  			while(left<right) {
  				//如果大于0要将数值减小
  				if (nums[i] + nums[left] + nums[right] > 0) {
  					right--;
  				}
  				//小于零要将数值增大
  				else if (nums[i] + nums[left] + nums[right] < 0) {
  					left++;
  				}
  				//等于零要将值存进三元组，同时收缩left和right
  				else {
  					result.push_back(vector<int>{nums[i], nums[left], nums[right]});
  					//第二次去重，对三元组中的两个元素进行去重
  					//这里面把指针移动到唯一的right和left处
  					//再进行加一，进行下一个循环
  					while (right > left && nums[right] == nums[right - 1]) {
  						right--;
  					}
  					while (right > left && nums[left] == nums[left + 1]) {
  						left++;
  					}
  					right--;
  					left++;
  				}
  			}
  			
  		}
  		return result;
  	}
  };
  

四数之和

• 思路：

  四数之和的思路和三数之和的思路一样

  这两个之间就是通过双指针法把原本的时间复杂度降低一个等级

• 注意：

  • 注意剪枝和去重

    

    剪枝得时候注意，由于target是未知的，不可以直接用首元素大于target来进行剪枝

    不然会出现-4>-10，但是数组接下来的几个数都是负数

    但是还是可以进行剪枝

    剪枝的本质就是正数的大于是无法再合成targrt的，不用target>0是因为剪枝不彻底，会漏掉target<0，但是第一个元素已经大于0的情况，用首元素大于0，且大于target是合理的。

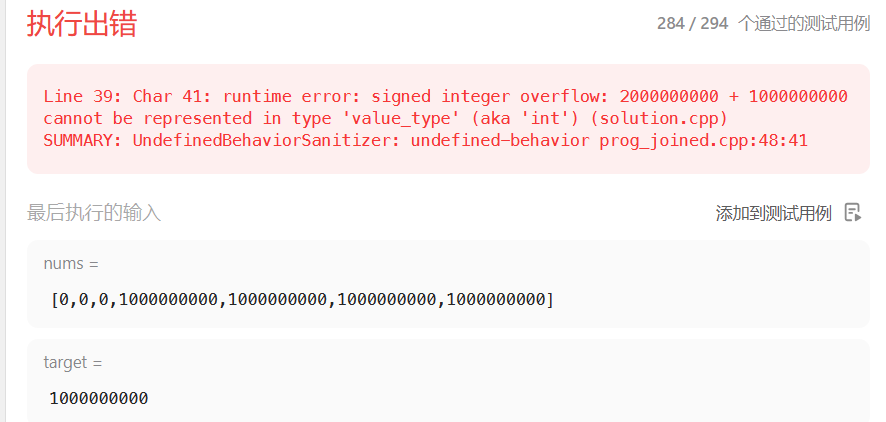
  • 注意四数之和相加得时候会出现数组越界，这个时候要用long，不然比较溢出

  

• 代码：

  class Solution {
  public:
  	vector<vector<int>> fourSum(vector<int>& nums, int target) {
  		//定义一个返回的数组值
  		vector<vector<int>> result;
  
  		//首先对数组进行排序
  		sort(nums.begin(), nums.end());
  
  		//第一层循环
  		for (int i = 0; i < nums.size(); i++) {
  			//第一层剪枝
  			//如果第一个数就大于0，那就一定不会有四数之和等于0
  			//这里不可以直接用这个剪枝，因为target是一个未确定的值
  			if (nums[i] > target && nums[i] >= 0) {
  				//这里用break，最后再统一返回
  				break;
  			}
  			//第一次去重
  			if (i > 0 && nums[i] == nums[i - 1]) {
  				continue;
  			}
  			//第二层循环
  			for (int j = i + 1; j < nums.size(); j++) {
  				//第二次剪枝,如果最开始的两个数加在一起都大于target
  				if (nums[i] + nums[j] > target && nums[i] >= 0) {
  					//跳出当前所有循环
  					break;
  				}
  				//第二次去重
  				if (j > i + 1 && nums[j] == nums[j - 1]) {
  					//继续本次循环的下一次循环
  					continue;
  				}
  				//寻找两个数的和
  				int left = j + 1;
  				int right = nums.size() - 1;
  				while (left < right) {
  					if ((long)nums[i] + nums[j] + nums[left] + nums[right] > target) {
  						right--;
  					}
  					else if ((long)nums[i] + nums[j] + nums[left] + nums[right] < target) {
  						left++;
  					}
  					else {
  						//将此数组存进result中
  						result.push_back(vector<int>{nums[i], nums[j], nums[right], nums[left]});
  						//第三次去重
  						while (left < right && nums[left] == nums[left + 1]) {
  							left++;
  						}
  						while (left < right && nums[right] == nums[right - 1]) {
  							right--;
  						}
  						left++;
  						right--;
  					}
  				}
  			}
  		}
  		return result;
  	}
  };
  

双指针总结

• 数组
  • 数组不可以凭空消失，只能进行覆盖，移除查找的时候用双指针法
• 字符串
  • 双指针法
• 链表
  • 快慢指针法
  • 双指针法
• N数之和法
  • 双指针法
  • 哈希法（其实用双指针法可以解决，但是用双指针法求下标不太ok，双指针会将表先进行排序，打乱下标，如果进行映射的话还会占用额外空间）

栈与队列

栈与队列理论基础

• 栈和队列是STL（c++标准库）里面的两个数据结构

  • STL是有多个版本的，只有知道使用的STL是哪个版本的才能知道对应的栈和队列的实现原理

    三个最为普遍的STL版本：

    • HP STL其他版本的C++ STL，一般是以HP STL为蓝本实现的，HP STL是C++ STL的第一个实现版本，且开放源代码
    • P.J.Planger STL是由P.J.Plaunger参照HP STL实现出来的，被Visual C++编译器所采用，不是开源的
    • SGL STL是由Silicon Graphics Computer Systems公司参照HP STL实现，被Linux的C++编译器GCC所采用，SGL STL是开源软件，源码可读性甚高。

  • 关于SGI STL里面的数据结构

    • 栈

      栈先进后出，提供push和pop等接口，不提供走访功能，不提供迭代器。

      栈是以底层容器来完成其所有的工作，对外提供统一的接口，底层容器是可插拔的（也就是说我们可以控制使用哪种容器来实现栈的功能）。

      STL一般不被归为容器，而是容器适配器（container adapter）

      栈的内部结构可以是vector， deque， list，主要就是数组和链表的底层实现

      

      • SGI STL如果没有指定底层实现的话，默认是以deque为缺省情况下栈的底层结构。

        deque是一个双向队列，只要封住一段，开通另一端就可以实现栈的逻辑了

      
      

用栈实现队列

• 思路：用栈，一个模仿进队列，一个模仿出队列
• 注意：
• 代码：

用队列实现栈

• 思路：用一个队列，将最后一个元素前面的元素重新插入队列，

• 注意：

• 代码：

  class MyStack {
  public:
  	queue<int> que;
  
  	MyStack() {
  
  	}
  
  	void push(int x) {
  		que.push(x);
  	}
  
  	int pop() {
  		//将队首元素重新插回到队尾
  		int size = que.size();
  		size--;
  		for (int i = 0; i < size; i++) {
  			int temp = que.front();
  			que.push(temp);
  			que.pop();
  		}
  		int num = que.front();
  		que.pop();
  		return num;
  	}
  
  	int top() {
  		int size = que.size();
  		size--;
  		for (int i = 0; i < size; i++) {
  			int temp = que.front();
  			que.push(temp);
  			que.pop();
  		}
  		int num = que.front();
  		que.pop();
  		que.push(num);
  		return num;
  	}
  
  	bool empty() {
  		return que.empty();
  	}
  };
  

有效的括号

• 思路：利用栈的特性实现括号匹配

• 注意：通过一些巧妙的方式利用栈，多练，无他

• 代码：

  class Solution {
  public:
  	bool isValid(string s) {
  		//如果括号是偶数，一定不符合条件
  		if (s.size() % 2 != 0) {
  			return false;
  		}
  		stack<char> string;
  		for (int i = 0; i < s.size(); i++) {
  			if (s[i] == '(') {
  				string.push(')');
  			}
  			else if (s[i] == '[') {
  				string.push(']');
  			}
  			else if (s[i] == '{') {
  				string.push('}');
  			}
  			else {
  				if (string.empty()||string.top() != s[i]) {
  					return false;
  				}
  				string.pop();
  			}
  		}
  		return string.empty();
  	}
  };
  

删除字符串中的所有相邻重复项

• 思路：同括号匹配原理相似

• 注意：用字符串也可以实现栈的功能

• 代码：

  class Solution {
  public:
  	string removeDuplicates(string S) {
  		string result;
  		for (char s : S) {
  			//当字符串为空或者当前字符不相等的时候
  			if (result.empty() || result.back() != s) {
  				result.push_back(s);
  			}
  			else {
  				result.pop_back();
  			}
  		}
  		return result;
  	}
  };
  

逆波兰表达式求值

• 思路：后缀表达式求和思想

• 注意：注意弹栈时候进行加减乘除的时候num1和num2是有顺序的

  stoll()函数是把字符串转化成longlong类型

• 代码：

  class Solution {
  public:
  	int evalRPN(vector<string>& tokens) {
  		stack<long long> st;
  		long long num1;
  		long long num2;
  		int size = tokens.size();
  		for (int i = 0; i < size; i++) {
  			if(tokens[i] == "+"||tokens[i] == "-"|| tokens[i] == "*"|| tokens[i] == "/"){
  				num1 = st.top();
  				st.pop();
  				num2 = st.top();
  				st.pop();
  				if (tokens[i] == "+") st.push(num2 + num1);
  				if (tokens[i] == "-") st.push(num2 - num1);
  				if (tokens[i] == "*") st.push(num2 * num1);
  				if (tokens[i] == "/") st.push(num2 / num1);
  			}
  			else {
  				//stoll()将字符串转成longlong的整数
  				st.push(stoll(tokens[i]));
  			}
  		}
  		return st.top();
  	}
  };
  

滑动窗口最大值（困难）

• 思路：

  单调队列：保证队列里的元素单调递增或单调递减的原则

• 注意：

  • if主要用于判断，while用于迭代
  • 实际上时间复杂度是O(n)

• 代码：

  class Solution {
  private:
  	class MyQueue {
  	public:
  		deque<int> que;
  		//每次弹出的时候，比较当前要弹出的数值是否等于队列出口的元素的数值，如果相等则弹出
  		//pop之前要判断队列是否为空
  		void pop(int value) {
  			//相等的时候可以弹出，如果不相等，证明这个数现在不是最大值，没有在队列里面或者在后面
  			//可以不用弹出
  			//如果相等说明最大值弹出了
  			if (!que.empty() && value == que.front()) {
  				que.pop_front();
  			}
  		}
  		//push是从后往前插入
  		void push(int value) {
  			while (!que.empty() && que.back() < value) {
  				que.pop_back();
  			}
  			que.push_back(value);
  		}
  		//查询当前的最大值直接返回前端就可以了
  		int front() {
  			return que.front();
  		}
  	};
  public:
  	//实现一个单调队列
  
  	vector<int> maxSlidingWindow(vector<int>& nums, int k) {
  		MyQueue que;
  		vector<int> result;
  		//首先将前n个放入数组中
  		for (int i = 0; i < k; i++) {
  			que.push(nums[i]);
  		}
  		//开始将第一轮的最大元素输入到result
  		result.push_back(que.front());
  		//迭代
  		for (int i = k; i < nums.size(); i++) {
  			//移动滑动窗口
  			que.pop(nums[i-k]);
  			que.push(nums[i]);
  			//记录当前的最大值
  			result.push_back(que.front());
  		}
  		return result;
  	}
  };
  

前K个高频元素（思路）

• 思路：

  • 首先构建map，map用来统计数值出现的次数
  • 再将map中的元素进行排序寻找到前K个高频元素
    • 用小顶堆，小顶堆弹出最小的n个值，最终得到了前K个高频元素
  • 为什么不能用有序map呢？

• 注意：

  • map和小顶堆的实现
  • 有很多新的语法

• 代码：

  class Solution {
  public:
  	//定义了一个比较规则
  	class mycomparion {
  	public:
  		//pair是c++标准模板库中定义的一个模板类，用于表示一对值
  		//这个函数其实是定义了一种比较规则，按照两个pair数组的secound值的降序进行比较
  		bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
  			//如果lhs的secound值大于rhs的secound值，就返回true
  			return lhs.second > rhs.second;
  		}
  	};
  	vector<int> topKFrequent(vector<int>& nums, int k) {
  		//用map统计元素出现的频率
  		unordered_map<int, int> map;
  		for (int i = 0; i < nums.size(); i++) {
  			//这个里面key值是nums[i]
  			//value是key出现的次数
  			//对key进行排序并没有意义
  			//因此用无序map
  			map[nums[i]]++;
  		}
  
  		//对value值进行排序
  		//定义一个小顶堆，大小为k
  		//将所有频率的数值存进去，小的数值自然就被弹出
  		//priority_queue是一个容器适配器，用于实现基于某种比较的排序
  		//其底层实现逻辑是堆，保证头部永远是优先级最高的元素
  
  		//三个参数分别为，比较对象，存储比较对象的容器，比较逻辑
  		priority_queue < pair<int, int>, vector<pair<int, int>>,mycomparion> pri_que;
  
  		//用固定大小为k的小顶堆，扫描所有频率的数值
  		//::是作用域解析符用来指定特定的命名空间或类的成员
  		//iterator是unordered_map<int,int>数据结构中定义的迭代器，用于遍历map
  
  		for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {
  			//把其中的it指向的内容放进去
  			pri_que.push(*it);
  			if (pri_que.size() > k) {
  				pri_que.pop();
  			}
  		}
  		//小顶堆先输出的是最小的，采用倒叙来输出数组
  		vector<int> result(k);
  		for (int i = k - 1; i >= 0; i--) {
  			result[i] = pri_que.top().first;
  			pri_que.pop();
  		}
  		return result;
  	}
  };
  

栈与队列的总结

• 栈与队列的理论基础

  • 容器
    • deque（双端队列）
    • list（列表）
    • vector（数组）
  • 容器适配器
    • stack（栈）
    • queue（队列）
    • priority_queue{元素，元素容器，优先级规则}，（优先级队列）
  • 栈与队列的问题
    

• 总结
  • 单调队列
  • 优先级队列

二叉树

二叉树理论基础篇

• 题目分类

  • 二叉树的遍历方式
  • 二叉树的属性
  • 二叉树的修改与构造
  • 求二叉树的搜索属性
  • 二叉树的公共祖先问题
  • 二叉搜索树的修改与构造

• 二叉树的类型

  • 满二叉树

  • 完全二叉树

  • 二叉搜索树

  • 平衡二叉搜索树

    C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，unordered_map、unordered_set，unordered_map、unordered_set底层实现是哈希表。

• 二叉树的存储方式

  • 链式存储
  • 顺序存储

• 二叉树的遍历方式

  栈其实就是递归的一种实现结构

  • 深度优先遍历
    • 前序遍历（递归法，迭代法）
    • 中序遍历（递归法，迭代法）
    • 后序遍历（递归法，迭代法）
  • 广度优先遍历
    • 层次遍历（迭代法）

• 二叉树的定义方式

    struct TreeNode {
        int val;
        TreeNode *left;
        TreeNode *right;
        //初始化的时候左右指针为空
        TreeNode(int x) : val(x), left(NULL), right(NULL) {}
    };
  

• 总结

  二叉树是一种基础数据结构

二叉树的递归遍历

• 思路：

  递归的思路：

  1.确定递归函数的参数和返回值

  2.确定中止条件

  3.确定单层递归逻辑

• 注意：

• 代码：

二叉树的迭代遍历

• 思路：
• 注意：
• 代码：

二叉树的统一迭代法

• 思路：
• 注意：
• 代码：

二叉树层序遍历

二叉树的层序遍历

• 思路：层序遍历的底层逻辑是队列，先进先出

• 注意：

• 代码：

  模板代码（打十个）

  vector<vector<int>> levelOrder(TreeNode* root) {
  	//定义一个存放Treenode指针的队列
  	queue<TreeNode*> que;
  	//如果root不为空的时候将，root入队
  	if (root != NULL) {
  		que.push(root);
  	}
  	//返回的是每一层
  	vector<vector<int>> result;
  	//遍历直到队列为空
  	while (!que.empty()) {
  		int size = que.size();
  		vector<int> layer;
  		for (int i = 0; i < size; i++) {
  			TreeNode* temp = que.front();
  			que.pop();
  			layer.push_back(temp->val);
  			if (temp->left != NULL) {
  				que.push(temp->left);
  			}
  			if (temp->right != NULL) {
  				que.push(temp->right);
  			}
  		}
  		result.push_back(layer);
  	}
  	return result;
  }
  

二叉树的层序遍历II

• 思路：

  这种方式会超出内存限制

  用一个栈去存储结果

  队列出队顺序层，右，左

  入栈之后再出栈顺序，左，右，层

  如果用栈的话如何进行分层呢

  直接用队列，然后最后将result数组进行反转

• 注意：

  反转数组的函数

二叉树的右视图

• 思路：

  层次遍历，但是只把最右的节点入栈，把每一层的最后一个节点入栈

• 注意：代码细节注意

二叉树的层平均值

• 思路：每一层的数相加，相除
• 注意：

N叉树的层序遍历

• 思路：

  Node的数据结构是，存储节点的值，存储一个children数组

• 注意：

在每个树行中找最大值

• 思路：

  层次遍历，找每一层的最大值

• 注意：

  //INT_MIN是c++标准库中定义的宏常量，通常是一个最小的负数值，用来求最大值的时候定义初始量
  int max = INT_MIN;
  

填充每个节点的下一个右侧节点指针

• 思路：

  将next指针指向同层的下一个节点

  层次遍历，每一层队列不为空的时候指向下一个节点，队列为空的时候指向NULL

• 注意：

填充每个节点的下一个右侧节点指针II

• 思路：完全二叉树和非完全二叉树没有什么区别
• 注意：

二叉树的最大深度

• 思路：
  • 层次遍历，计算总共有多少层
  • 递归，求左子树和右子树的最大深度，取最大值+1返回depth
• 注意：

二叉树的最小深度

• 思路：
  • 层次遍历，如果有一个节点是叶节点就返回深度
  • 递归，注意与求最大深度的单层递归逻辑不同，如果左子树为空，右子树不为空，返回的值应该是右子树的深度+1，而不是深度为1
• 注意：

翻转二叉树（拓展部分，中序遍历不可以）

• 思路：

  递归实现

• 注意：

  注意递归出口和递归条件

• 代码：

  TreeNode* invertTree(TreeNode* root) {
  	//递归出口
  	if (root == NULL) {
  		return root;
  	}
  	//递归体
  	swap(root->left, root->right);
  	invertTree(root->left);
  	invertTree(root->right);
  }
  

对称二叉树

• 思路：

  • 递归

    • 确定递归函数的参数和返回值

      比较左右两棵子树是不是对称的

      比较的不是左右孩子，而是左右子树的对称节点

    • 确定终止条件

      首先处理空结点，非空结点比较的是数值

      左节点为空，右节点不为空，false

      左节点不为空，右节点为空，false

      左右节点都为空，对称，返回true

    • 确定单层递归逻辑

      处理节点不为空的时候，比较val的值

      并且将左节点的左孩子和右节点的右孩子进行比较

      左节点的右孩子和右节点的左孩子进行比较

  • 队列

  • 栈

• 注意：注意代码细节

• 代码：

  • 递归法

  bool compare(TreeNode* left, TreeNode* right) {
  	//判出条件
  	if (left == NULL && right == NULL) {
  		return true;
  	}
  	else if (left == NULL && right != NULL) {
  		return false;
  	}
  	else if (left != NULL && right == NULL) {
  		return false;
  	}
  	else if (left->val != right->val) {
  		return false;
  	}
  	//此时是左右节点都不为空，且数值相同的情况
  	//此时做递归判断
  	//只有左右递归都返回true的时候才返回true；
  	bool L = compare(left->left, right->right);
  	bool R = compare(left->right, right->left);
  	return L && R;
  }
  bool isSymmetric(TreeNode* root) {
  	if (root == NULL) {
  		return true;
  	}
  	return compare(root->left, root->right);
  }
  

完全二叉树的节点个数

• 思路：

  • 递归：分别计算左子树和右子树有多少个节点，再相加
  • 层序遍历：统计总共遍历了多少层

• 注意：

  //这样的代码是错误的
  //忽略掉了一些情况
  int countRecursion(TreeNode* left, TreeNode* right) {
  	//判出条件
  	if (left == NULL && right != NULL) {
  		return 1 + countRecursion(right->left, right->right);
  	}
  	else if (left != NULL && right == NULL) {
  		return 1 + countRecursion(left->left, left->right);
  	}
  	else if (left == NULL && right == NULL) {
  		return 1;
  	}
  
  	//这个时候就是左右节点都非空结点
  	int num = countRecursion(left->left, right->right) + 1;
  	return num;
  }
  int countNodes(TreeNode* root) {
  	if (root == NULL) {
  		return 0;
  	}
  	return countRecursion(root->left, root->right);
  }
  

• 代码：

  int countNodes(TreeNode* root) {
  	//判出条件
  	if (root == NULL) {
  		return 0;
  	}
  	int left = countNodes(root->left);
  	int right = countNodes(root->right);
  	int num = left + right + 1;
  	return num;
  }
  

平衡二叉树

• 思路：

  • 平衡二叉树：左右两棵子树的高度之差小于1

  • 递归：一棵树是平衡二叉树，它的左右子树也是平衡二叉树

    如果直接返回true和false逻辑很复杂

    应该直接把函数分成两步，判断树是不是平衡二叉树，将左右两个树的判断结果进行与运算

    //存在逻辑错误的代码
    bool isBalanced(TreeNode* root) {
    	//递归出口
    	if (root == NULL) {
    		return true;
    	}
    	else {
    		int lefthigh = treeHigh(root->left);
    		int righthigh = treeHigh(root->right);
    		if (lefthigh >= righthigh) {
                //在这一行会直接返回，永远不会达到right && left
    			return (lefthigh - righthigh) <= 1;
    		}
    		else {
    			return (righthigh - lefthigh) <= 1;
    		}
    	}
    	bool right = isBalanced(root->right);
    	bool left = isBalanced(root->left);
    	return right && left;
    }
    

  • 迭代：手动实现一个栈，用迭代的方法再写一遍

• 注意：

• 代码：

  int treeHigh(TreeNode* root) {
  	//用层次遍历求树的高度
  	queue<TreeNode*> que;
  	int num = 0;
  	if (root != NULL) {
  		que.push(root);
  	}
  	TreeNode* temp;
  	while (!que.empty()) {
  		int size = que.size();
  		for (int i = 0; i < size; i++) {
  			temp = que.front();
  			que.pop();
  			if (temp->left != NULL) {
  				que.push(temp->left);
  			}
  			if (temp->right != NULL) {
  				que.push(temp->right);
  			}
  		}
  		//执行一次for循环就证明遍历了一个层
  		num++;
  	}
  	return num;
  }
  bool isBalanced(TreeNode* root) {
  	//递归出口
  	if (root == NULL) {
  		return true;
  	}
  	else {
  		int lefthigh = treeHigh(root->left);
  		int righthigh = treeHigh(root->right);
  		if (lefthigh >= righthigh) {
  			if (lefthigh - righthigh > 1) {
  				return false;
  			}
  		}
  		else {
  			if (righthigh - lefthigh > 1) {
  				return false;
  			}
  		}
  	}
  	bool right = isBalanced(root->right);
  	bool left = isBalanced(root->left);
  	return right && left;
  }
  

二叉树的所有路径

• 思路：

  回溯

  回溯和递归是一一对应的，有一个递归就要有一个回溯，递归和回溯要永远在一起

  这道题目要求从根节点到叶子的路径，用前序遍历

  递归：

  1.要传入根节点，记录每一条路径的path和存放结果集的string

  2.确定递归的终止条件

  本题是要找到叶子节点，不让cur指向NULL

  中止的时候，把vector中的数据转化称string存入vector数组中，函数进行回溯调用，继续寻找下一条路径。

  3.先存根节点

  如果根节点的左右节点为控，递归的时候就不进行下一层递归了

  否则将左右节点加入，进行下一层递归，当达成判出条件的时候，要进行回溯

  一个递归一个回溯，因此这里递归要加在花括号之前

  //错误写法
  //只有一条路径，最后pop_back一个数据，并没有起到回溯的作用
  if (cur->left) {
   traversal(cur->left, path, result);
  }
  if (cur->right) {
   traversal(cur->right, path, result);
  }
  path.pop_back();
  
  //正确写法
  //回溯的时候，先往右走，然后右节点如果存在，再递归加入右节点的路径
  if (cur->left) {
   traversal(cur->left, path, result);
   path.pop_back(); // 回溯
  }
  if (cur->right) {
   traversal(cur->right, path, result);
   path.pop_back(); // 回溯
  }
  

• 注意：

  精简代码，二刷时候看一下

• 代码：

  	void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
  		//将cur压入栈中
  		path.push_back(cur->val);
  		//判出条件
  		if (cur->left == NULL && cur->right == NULL) {
  			string spath;
  			for (int i = 0; i < path.size() - 1; ++i) {
  				spath += to_string(path[i]);
  				spath += "->";
  			}
  			spath += to_string(path[path.size() - 1]);
  			result.push_back(spath);
  		}
  		//递归体
  		//左
  		if (cur->left != NULL) {
  			traversal(cur->left, path, result);
  			path.pop_back();
  		}
  		//右
  		if (cur->right != NULL) {
  			traversal(cur->right, path, result);
  			path.pop_back();
  		}
  	}
  	vector<string> binaryTreePaths(TreeNode* root) {
  		vector<int> path;
  		vector<string> result;
  		if (root == NULL) {
  			return result;
  		}
  		traversal(root, path, result);
  		return result;
  	}
  

左叶子之和

• 思路：

  首先判断什么是左叶子，左叶子首先是左孩子，其次左右节点为空

  因此判断是不是左叶子要看它的父节点

• 注意：

• 代码：

  	int sumOfLeftLeaves(TreeNode* root) {
  		//判出条件
  		if (root == NULL) {
  			return 0;
  		}
  		if (root->left == NULL && root->right == NULL) {
  			return 0;
  		}
  		//递归体
  		int leftValue = sumOfLeftLeaves(root->left);
  		//当左子树是左叶子的时候，修改左子树的值
  		if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) {
  			leftValue = root->left->val;
  		}
  		int rightValue = sumOfLeftLeaves(root->right);
  		return leftValue + rightValue;
  	}
  

找树左下角的值（二刷用递归写）

• 思路：

  层序遍历：最后一层中的第一个节点

  递归：

  递归到最左边要判断是不是最后一行

  1.确定递归函数的参数和返回值

  2.确定终止条件

  3.确定单层递归的逻辑

• 注意：

• 代码：

  层序遍历

  int findBottomLeftValue(TreeNode* root) {
          queue<TreeNode*> que;
          int result;
          que.push(root);
          while (!que.empty()) {
              int size = que.size();
              TreeNode* left = que.front();
              result = left->val;
              for (int i = 0; i < size; i++) {
                  TreeNode* temp = que.front();
                  que.pop();
                  if (temp->left != NULL) {
                      que.push(temp->left);
                  }
                  if (temp->right != NULL) {
                      que.push(temp->right);
                  }
              }
          }
          return result;
      }
  

  递归

路径总和

• 思路：

  递归+回溯

  如果父节点不拎出来判断，root = NULL并不是返回的条件，叶子节点才是返回的条件

  栈模拟：有空写一下

• 注意：

• 代码：

  bool travel(TreeNode* root, int count) {
  	//递归出口
  	if (root->left == NULL && root->right == NULL) {
  		return count == 0;
  	}
  	//左节点
  	if (root->left != NULL) {
  		count -= root->left->val;
  		if (travel(root->left, count)) {
  			return true;
  		}
  		//如果到这一步证明该节点下不存在路径，回溯
  		count += root->left->val;
  	}
  	//右节点
  	if (root->right != NULL) {
  		count -= root->right->val;
  		if (travel(root->right, count)) {
  			return true;
  		}
  		count += root->right->val;
  	}
  	//遍历到这证明左右子树都没有路径
  	return false;
  }
  bool hasPathSum(TreeNode* root, int targetSum) {
  	if (root == NULL) {
  		return false;
  	}
  	//这个时候已经把根节点加入路径了
  	return travel(root, targetSum - root->val);
  }
  

路经总和II

• 思路：

  同路径总和不同的是，这个需要找出所有的路径，递归不要返回值

• 注意：

  注意根节点的处理，先把根节点放入path中，如果path递归到最后count不为0，这个path不会放到result中。

• 代码：

  class Solution {
  private:
  	vector<vector<int>> result;
  	vector<int> path;
      void travel(TreeNode* root, int count) {
  	//当遇到叶子节点的时候
  	if (!root->left && !root->right && count == 0) {
  		//路径结束，且是正确路径
  		result.push_back(path);
  	}
  	//左节点
  	if (root->left) {
  		//先将左节点入栈
  		path.push_back(root->left->val);
  		count -= root->left->val;
  		travel(root->left, count);
  		count += root->left->val;
  		path.pop_back();
  	}
  	//右节点
  	if (root->right) {
  		path.push_back(root->right->val);
  		count -= root->right->val;
  		travel(root->right, count);
  		count += root->right->val;
  		path.pop_back();
  	}
  	return;
  }
  public:
  vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
  	if (root == NULL) {
  		return result;
  	}
      path.push_back(root->val);
  	travel(root, targetSum - root->val);
  	return result;
  }
  };
  

从中序与后序遍历序列构造二叉树

• 思路：

  • 后序的最后一个元素确定根
  • 中序根据根进行切分，然后将后序分成两个部分
  • 递归，分成的左右两个部分分别重复1，2步骤直到后序剩最后一个元素

• 注意：

  • 切割数组的时候要遵循一个原则，不然会漏掉元素，和二分法的准则一样。
  • 中序数组和后序数组的大小相等。

• 代码：

  • 代码遵循左闭右开 的原则。

class Solution
{
private:
    // traversal函数的目的是找到当前队列的根节点，并且返回的是左右指针已经链接好的根节点
    TreeNode *traversal(vector<int> &inorder, int inorderBegin, int inorderEnd, vector<int> &postorder, int postorderBegin, int postorderEnd)
    {
        // 判出条件
        if (postorderEnd - postorderBegin == 0)
        {
            return NULL;
        }

        // 取出后序遍历的最后一个节点
        int rootValue = postorder[postorderEnd-1];
        TreeNode *root = new TreeNode(rootValue); // 构造函数初始化就是左右指针指向空

        // 当后序遍历只剩下这一个节点的时候证明是叶子节点，入队
        if (postorderEnd - postorderBegin == 1)
        {
            return root;
        }

        // 找到中序遍历的切割点下标
        int inorderIndex;
        for (inorderIndex = 0; inorderIndex < inorder.size(); ++inorderIndex)
        {
            if (inorder[inorderIndex] == rootValue)
                break;
        }

        // 切割中序数组，得到中序左数组和中序右数组
        // 左中序区间
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = inorderIndex;
        // 右中序区间
        int rightInorderBegin = inorderIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割后序数组，得到后序左数组和后序右数组
        // 后序左数组
        int leftPostorderBegin = postorderBegin;
        int leftPostorderEnd = postorderBegin + leftInorderEnd - leftInorderBegin; // 起始位置加上中序遍历的元素个数
        // 后序右数组
        int rightPostorderBegin = postorderBegin + leftInorderEnd - leftInorderBegin ;
        int rightPostorderEnd = postorderEnd - 1;

        // 遍历得到左右子树
        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);

        return root;
    }

public:
    //buildTree返回的就是要入队的根节点
    TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder)
    {
        if(inorder.size() == 0||postorder.size() == 0){
            return NULL;
        }
        return traversal(inorder,0,inorder.size(),postorder,0,postorder.size());
    }
};

补充：105.从前序与中序遍历序列构造二叉树

最大二叉树

• 思路：

  • 构造二叉树一般采用前序遍历，先遍历根节点再设置左右节点。

• 注意：

  • 采用传一个数组+传数组下标值的范围，避免数组的来回拷贝。

• 代码：

class Solution
{
private:
    TreeNode *traversal(vector<int> &nums, int left, int right)
    {
        // 构造二叉树一般用前序遍历，先构造根节点，再构造左右子树的节点

        // 递归出口
        if (left >= right)
        {
            return NULL;
        }
        // 找出这个数组区间内的最大值，保持左闭右开的原则
        //最右边的那个数已经被用了
        int maxIndex = left;
        for (int i = left + 1; i < right; ++i)
        {
            if(nums[i]>nums[maxIndex]){
                maxIndex = i;
            }
        }
        //找到最大值和分割下标
        int rootValue = nums[maxIndex];
        TreeNode* root = new TreeNode(rootValue);
        
        root->left = traversal(nums,left,maxIndex);
        root->right = traversal(nums,maxIndex+1,right);
        return root;
    }

public:
    TreeNode *constructMaximumBinaryTree(vector<int> &nums)
    {
        return traversal(nums,0,nums.size());
    }
};

合并二叉树

• 思路：

  • 二叉树使用递归就要优先想使用前中后哪种遍历方式
  • 构建和操作二叉树用前序遍历的比较多

• 注意：

• 代码：

class Solution
{
private:
    
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1 == NULL){
            return root2;
        }
        if(root2 == NULL){
            return root1;
        }
        //两个都不为空的时候
        TreeNode* root = new TreeNode(root1->val+root2->val);
        root->left = mergeTrees(root1->left,root2->left);
        root->right = mergeTrees(root1->right,root2->right);
        return root;
    }
};

二叉搜索树中的搜索

• 思路：

  • 二叉搜索数是有序的数组，左小右大
  • 利用递归的方式写

• 注意：

• 代码：

class Solution
{
private:
    
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        //确定递归的判出条件
        if(root == NULL||root->val == val){
            return root;
        }

        if(root->val > val){
            return searchBST(root->left,val);
        }
        if(root->val < val){
            return searchBST(root->right,val);
        }
        return NULL;
    }
};

验证二叉搜索树

• 思路：

  • 中序遍历二叉搜索树，就变成了检验一个数组是不是递增的。

• 注意：

  • 在判断是不是递增序列的时候，最好用i和i-1进行判断，防止数组越界。

• 代码：

class Solution
{
private:
    vector<int> result;
    void traversal(TreeNode* root){
        //递归出口
        if(root == NULL){
            return;
        }
        //左
        traversal(root->left);
        //根
        result.push_back(root->val);
        traversal(root->right);
    }
public:
    bool isValidBST(TreeNode* root) {
        //中序遍历数组
        traversal(root);
        //判断数组是不是递增的数组
        for(int i = 1;i < result.size();++i){
            if(result[i] <= result[i-1]){
                return false;
            }
        }
        return true;
    }
};

二叉搜索树的最小绝对差

• 思路：

  • 二叉搜索树求边的最小值

• 注意：

• 代码：

class Solution
{
private:
    int result = INT_MAX;
    TreeNode *pre = NULL;
    void traversal(TreeNode *cur)
    {
        if (cur == NULL)
        {
            return;
        }
        // 左
        traversal(cur->left);
        // 中
        if (pre != NULL)
        {
            result = min(result, cur->val - pre->val);
        }
        pre = cur;
        // 右
        traversal(cur->right);
    }

public:
    int getMinimumDifference(TreeNode *root)
    {
        traversal(root);
        return result;
    }
};

二叉搜索树中的众数

• 思路：

  • 重点是把数组遍历一遍，用哪种遍历都行
  • 考虑到二叉搜索树的特殊性质，中序遍历统计相同的元素出现的次数就可以了
  • 考虑众数可能有多个，设置数组存储结果集
  • 当出现次数相同且当前次数最大的时候，将元素当如结果集，当出现更大的元素的时候要清空结果集

• 注意：

• 代码：

class Solution
{
private:
    //出现的最大的次数
    int maxCount = 0;
    //统计出现的次数
    int count = 0;
    //结果数组集
    vector<int> result;
    //记录父节点
    TreeNode* pre = NULL;
    //递归
    void traversal(TreeNode* root){
        //递归出口
        if(root == NULL){
            return;
        }
        //左
        traversal(root->left);
        //中
        //第一个节点
        if(pre == NULL){
            count = 1;
        }else if(pre->val == root->val){
            //相同的话计数器++
            ++count;
        }else{
            //不同的话直接从1开始计数
            count = 1;
        }
        pre = root;
        if(count == maxCount){
            result.push_back(root->val);
        }
        if(count > maxCount){
            maxCount = count;
            result.clear();
            result.push_back(root->val);
        }
        //右
        traversal(root->right);
        return;
    }

public:
    vector<int> findMode(TreeNode* root) {
        count = 0;
        maxCount = 0;
        pre = NULL;
        result.clear();
        traversal(root);
        return result;
    }
};

二叉树的最近公共祖先

• 思路：

  • 左右根的回溯过程
  • 判出条件：当当前节点是p/q/NULL时，直接返回节点，找到了/没找到/遍历到叶子节点
  • 判断当前根的左子树是不是p/q，如果有的话直接返回p/q的值代表找到了
  • 判断当前根的右子树是不是p/q，如果有的话直接返回p/q的值代表找到了
  • 如果当前根的左右子树找到了p和q，那证明这个就是最近的公共节点
  • 如果当前根的左/右子树只找到了一个节点，那就返回p/q节点，代表找到了p/q节点
  • 如果左右子树都没找到，就返回NULL，代表没找到

• 注意：

  • 🔔递归函数有返回值时
    • 遍历某条边：

      if (递归函数(root->left)) return ;
      
      if (递归函数(root->right)) return ;
      

    • 搜索整棵树：

      left = 递归函数(root->left);  // 左
      right = 递归函数(root->right); // 右
      left与right的逻辑处理;         // 中 
      

  • 🔔后序遍历是天生的回溯，左右根。

• 代码：

class Solution
{
private:
    
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //判出条件，代表找没找到
        if(root == p||root == q||root == NULL){
            return root;
        }
        //遍历左子树
        TreeNode* left = lowestCommonAncestor(root->left,p,q);
        //遍历右子树
        TreeNode* right = lowestCommonAncestor(root->right,p,q);
        //中
        if(left!=NULL&&right!=NULL){
            return root;
        }else if(left == NULL&&right!=NULL){
            return right;
        }else if(left != NULL && right == NULL){
            return left;
        }else{
            return NULL;
        }
    }
};

二叉搜索树的最近公共祖先

• 思路：

  • 二叉搜索树的性质是有大小的，因此从上向下进行遍历，遇到数值在p，q之间证明这个节点是p，q的公共祖先
  • 并且因为此时这个节点在p，q中间，p，q一定在它的左右子树上，所以这个节点就是最近的公共祖先

• 注意：

• 代码：

class Solution
{
private:
    
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //遍历整个树要把left和right接住
        //递归出口
        if(root == NULL){
            return NULL;
        }
        //左
        if(root->val>max(p->val,q->val)){
            TreeNode* left = lowestCommonAncestor(root->left,p,q);
            if(left!=NULL){
                return left;
            }
        }
        if(root->val<min(p->val,q->val)){
            TreeNode* right = lowestCommonAncestor(root->right,p,q);
            if(right!=NULL){
                return right;
            }
        }
    return root;
    }
};

二叉搜索树中的插入操作

• 思路：

  • 只要是二叉搜索树就可以，不用调节平衡，题目就被简化很多
  • 遍历节点，直到节点到达NULL的时候，在当前NULL节点的父节点上添加节点
  • 单层递归的逻辑：根据二叉搜索树的性质确定遍历的方向

• 注意：

  • 此递归函数可以不用返回父节点，，但是不返回父节点的话就要设置单独的节点进行存储，设置返回父节点比较容易懂一些。

• 代码：

class Solution
{
private:
    
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        //递归出口
        if(root == NULL){
            //返回插入的节点
            TreeNode* node = new TreeNode(val);
            return node;
        }
        //寻找插入节点的位置
        if(root->val > val){
            root->left = insertIntoBST(root->left,val);
        }
        if(root->val < val){
            root->right = insertIntoBST(root->right,val);
        }
        return root;
    }
};

删除二叉搜索树中的节点

• 思路：

  • 找到节点
  • 删除节点，并且保证二叉搜索树的性质不变
  • 递归三部曲：
    • 确定递归函数的参数以及返回值
    • 确定终止条件
    • 确定单层递归的逻辑

• 🔔注意：

  • 单层递归删除的逻辑总共有五种：
    • 第一种：没有找到删除的节点
    • 第二种：左右孩子都为空，直接删除节点，返回NULL为根节点
    • 第三种：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子节点为根节点
    • 第四种：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子节点为根节点
    • 第五种：左右孩子节点都不为空，左小右大，将删除节点的左子树放到删除节点右子树的最左侧叶子节点的左。

• 代码：

class Solution
{
private:
public:
    TreeNode *deleteNode(TreeNode *root, int key)
    {
        // 递归出口
        // 第一种情况，没有找到要删除的节点，直接返回NULL
        if (root == NULL)
        {
            return NULL;
        }
        // 要删除的节点是当前节点时，四种情况
        if (root->val == key)
        {
            // 第二种情况，删除节点为叶子节点吗，直接删除
            if (root->left == NULL && root->right == NULL)
            {
                delete root;
                return NULL;
            }
            // 第三种情况，删除节点有左节点无右节点
            if (root->left != NULL && root->right == NULL)
            {
                TreeNode *left = root->left;
                delete root;
                return left;
            }
            // 第四种情况，删除节点有右节点无左节点
            if (root->left == NULL && root->right != NULL)
            {
                TreeNode *right = root->right;
                delete root;
                return right;
            }
            // 第五种情况，删除节点有左右节点
            if (root->left != NULL && root->right != NULL)
            {
                TreeNode *left = root->left;
                // 找到右节点的最左叶子节点
                TreeNode *returnRight = root->right;
                TreeNode *right = root->right;
                while (right->left != NULL)
                {
                    right = right->left;
                }
                // 将左子树赋值给右子树的最左叶子节点的左
                right->left = left;
                delete root;
                return returnRight;
            }
        }
        // 要删除节点不是当前节点时
        if (root->val > key)
        {
            root->left = deleteNode(root->left, key);
        }
        if (root->val < key)
        {
            root->right = deleteNode(root->right, key);
        }
        return root;
    }
};

修剪二叉搜索树

• 思路：

  • 考虑情况
    
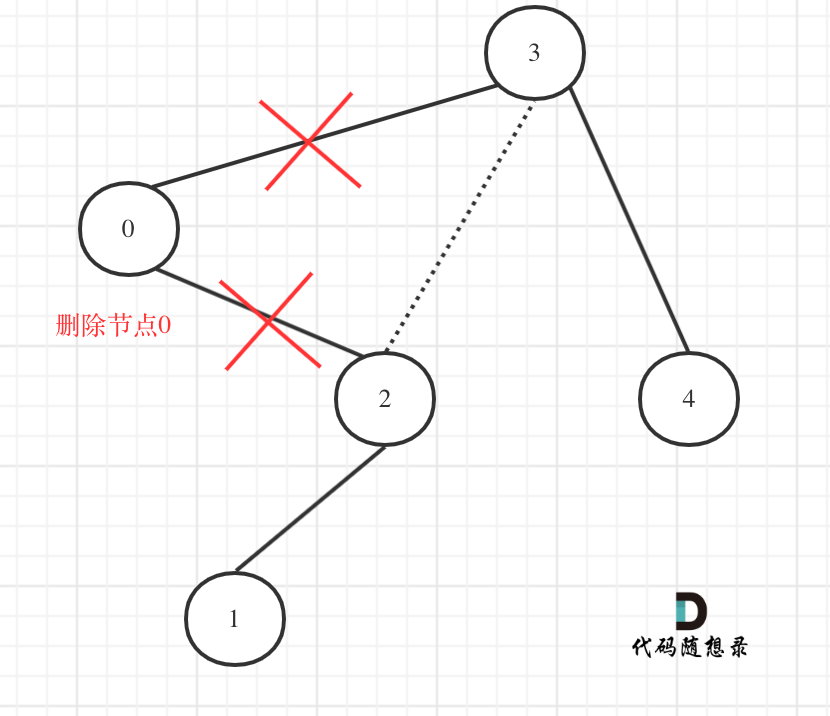
  • 直接将此节点的右子树连到父节点上即可。

• 注意：

• 代码：

class Solution
{
private:
    
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        //递归的出口
        if(root == NULL){
            return NULL;
        }
        //当当前节点超出范围，寻找要删除的节点有没有符合范围的节点值
        if(root->val < low){
            TreeNode* right = trimBST(root->right,low,high);
            return right;
        }
        if(root->val > high){
            TreeNode* left = trimBST(root->left,low,high);
            return left;
        }
        //遍历节点的左子树
        root->left = trimBST(root->left,low,high);
        //遍历节点的右子树
        root->right = trimBST(root->right,low,high);
        //当root节点以及root节点的左右子树都设置好之后，返回根节点
        return root;
    }
};

将有序数组转换为二叉搜索树

• 思路：

  • 构建高度平衡的二叉搜索树，取有序数组的中位数作为根节点
  • 递归遍历构建左右子树
  • 构建二叉树一般采用前序遍历

• 注意：

• 代码：

class Solution
{
private:
    //用左右的值来计算当前节点的下标，避免数组的反复拷贝
    TreeNode* traversal(vector<int>& nums,int left,int right){
        //递归出口，数组保持左闭右开原则
        if(left >= right){
            return NULL;
        }
        //根
        //创建新的节点
        int middle = (left + right)/2;
        TreeNode* node = new TreeNode(nums[middle]);

        //递归调用创建左子树
        node->left = traversal(nums,left,middle);
        node->right = traversal(nums,middle+1,right);
        return node;
    }
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return traversal(nums,0,nums.size());        
    }
};

把二叉搜索树转换为累加树

• 思路：

  • 首先确定遍历的顺序——由最大值累加，右中左
  • 这里也需要一个pre指针，累加的是当前节点和其pre的值

• 🔔注意：

  • 如果用一个返回值接住遍历右子树的值，无法处理右子树遍历到NULL的时候
  • 可以用判断右子树是不是NULL是NULL的话返回0，来解决

• 代码：

class Solution
{
private:
    int pre = 0;
    TreeNode* traversal(TreeNode* root){
        //判出条件
        if(root == NULL){
            return NULL;
        }
        //右
        // error，如果遇到空指针，会引发未定义行为，这也就是为什么要定义一个pre节点
        // int right = traversal(root->right)->val;
        //中
        traversal(root->right);
        root->val += pre;
        pre = root->val;
        //左
        traversal(root->left);
        return root;
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        return traversal(root);
    }
};

🌈 二叉树总结

• 涉及到二叉树的构造，无论普通二叉树还是二叉搜索树一定前序，都是先构造中节点
• 求普通二叉树的属性，一般是后序，一般要通过递归函数的返回值做计算
• 求二叉搜索树的属性，一定是中序，要充分利用二叉搜索树的有序性

回溯

🌈 回溯算法理论基础

• 回溯是递归的副产品，只要有回溯就会有递归

• 回溯的效率

  • 回溯的本质是穷举
  • 优化是剪枝

• 回溯法解决的问题

  • 组合问题：N个数里面按一定规则找出K个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 棋盘问题：N皇后，解数独等等

• 如何理解回溯法

  • 回溯法的问题都可以抽象理解为树形结构
  • 集合的大小就构成了树的宽度，递归的深度就构成了树的深度

• ⭐ 回溯法的模板

  • 类递归三部曲——确定函数返回值和参数、确定终止条件、确定单层递归逻辑。
  • 回溯函数模板返回值以及参数：回溯的参数不像二叉树递归一样比较容易确定，一般是先写逻辑，然后需要什么参数就填什么参数

    void backtracking(参数)
    

  • 回溯函数的终止条件

    if(终止条件){
    	存放结果；
    	return；
    }
    

  • 回溯搜索的遍历过程
    • 集合的大小构成了树的深度，递归的深度构成了树的深度

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
    }
    

    • 回溯完整模板

    void backtracking(参数) {
    	if (终止条件) {
    		存放结果;
    		return;
    	}
    
    	for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    		处理节点;
    		backtracking(路径，选择列表); // 递归
    		回溯，撤销处理结果
    	}
    }
    

组合

• 思路：

  • 暴力嵌套层数太多，难以写出来
  • 将组合问题抽象为树
    
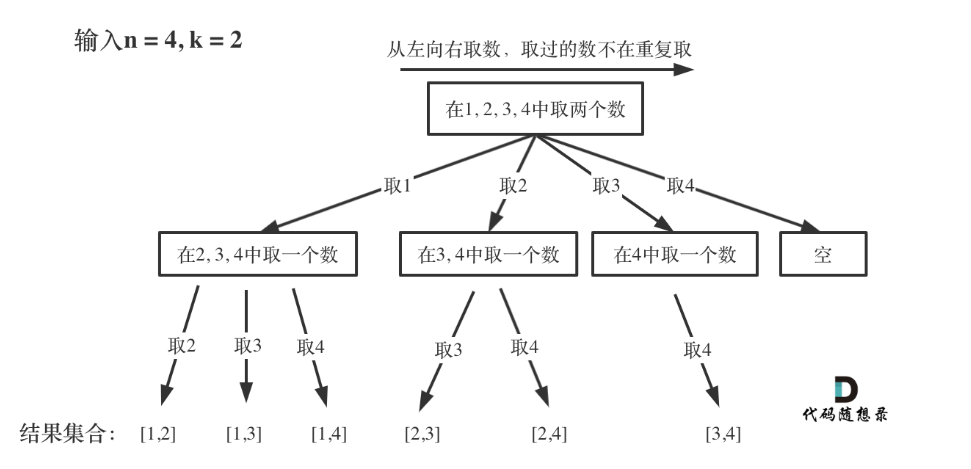
  • 图中可以发现n相当于树的宽度，k相当于树的深度
  • 图每次搜索到了叶子节点，就找到了一个结果。

• 🔔 注意：

  • 剪枝优化： 如果n = 4，k = 4的话，第一层for循环的时候，从元素2开始的遍历就都没有意义了，在第二层for循环，从元素3开始的遍历就都没有意义了。
    】

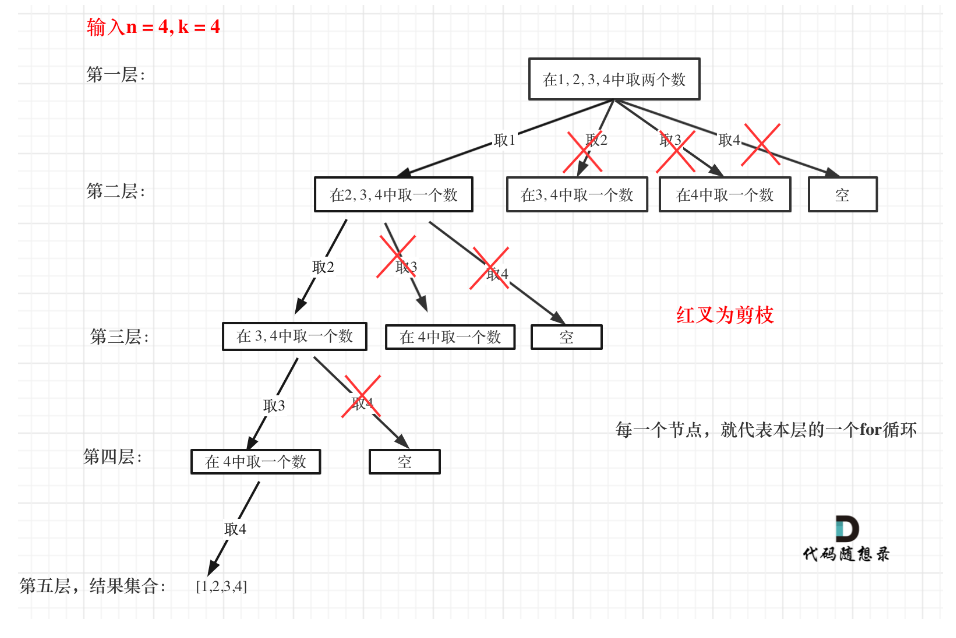    //剩下的还可以选就继续选，如果剩下的已经不足够达到目标的叶子节点的高度就剪枝
    for(int i = startIndex; i <= n - (k - path.size()) +1; i++)
    

• 代码：

class Solution
{
private:
    //定义两个数组，一个存放当前的结果，一个存放所有的结果
    vector<int> path;
    vector<vector<int>> result;
    //startIndex记录当前正在处理的节点
    void backtracking(int n, int k, int startIndex){
        //每次从startIndex开始遍历，然后用path保存取到的路径
        //中止条件，当path的值已经达到个数之后
        if(path.size() == k){
            result.push_back(path);
            return;
        }
        //回溯
        for(int i = startIndex;i<=n;i++){
            //处理节点
            path.push_back(i);
            //递归
            backtracking(n,k,i+1);
            //回溯，撤销处理结果
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
};

组合总和III

• 思路：

  • k个数代表了遍历的时候需要深度为k
  • 剪枝操作： 当当前的和已经大于sum的时候就不再进行遍历，可以加载递归函数开始的位置

• 注意：

• 代码：

class Solution
{
private:
    int sum = 0;
    vector<int> path;//记录结果的路径
    vector<vector<int>> result;//记录结果的集合
    void backtracking(int k,int n,int startIndex){
        //判出条件：当遍历的深度达到k的时候，判断path是不是要入栈，然后再返回
        if(path.size()==k){
            if(sum == n){
                result.push_back(path);
            }
            return;
        }
        //递归+回溯
        for(int i = startIndex; i <= 9 - (k - path.size()) + 1;++i){
            sum += i;//处理
            path.push_back(i);//处理
            //剪枝
            if(sum>n){
                sum -= i;
                path.pop_back();
                return;
            }
            //递归
            //这里是i+1而不是startIndex+1是因为是深度的扩展，而不是改变子树
            backtracking(k,n,i+1);
            //回溯
            //回溯的时候sum值也要回溯
            sum -= i;
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum3(int k, int n) {
        backtracking(k,n,1);
        return result;
    }
};

电话号码的字母组合

• 思路：

  • 字符串的size就是k，也就是二叉树的深度
  • 字符串的宽度是固定的每一个数字所对应的字母个数
  • 数字和字母建立映射

• 注意：

• 代码：

class Solution
{
private:
    const string map[10] = {
    "", // 0
    "", // 1
    "abc", // 2
    "def", // 3
    "ghi", // 4
    "jkl", // 5
    "mno", // 6
    "pqrs", // 7
    "tuv", // 8
    "wxyz", // 9
};
string s;
vector<string> result;
void backtracking(string digits,int startIndex){
    //判出条件，达到深度就判出
    if(s.size() == digits.size()){
        result.push_back(s);
        return;
    }
    //递归
    //取出digit
    int digit = digits[startIndex] - '0';
    //取出当前层要遍历的字符串
    string letters = map[digit];
    //对这一层去进行选择，因为是穷举，不用判断直接往里面填
    for(int i = 0;i<letters.size();i++){
        //处理节点
        s.push_back(letters[i]);
        backtracking(digits,startIndex+1);
        s.pop_back();
    }
}

public:
    vector<string> letterCombinations(string digits) {
        //一定要加这个判空判断，不然如果第一个元素没有意义，那就无法跳出递归
        if(digits.size() == 0){
            return result;
        }
        backtracking(digits,0);
        return result;
    }
};

组合总和

• 思路：

  • 在进行选择的时候要先将待选择的元素进行排序
  • 每次进行下一层待选择的元素是当前元素以及以后的元素，之前的元素不能被选择，不然会造成结果集重复

• 注意：

  • 在求和问题中，排序之后加剪枝是常见的套路

• 代码：

class Solution
{
private:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& candidates,int target,int sum,int startIndex){
        //判出条件
        if(sum == target){
            result.push_back(path);
            return;
        }
        //循环
        for(int i = startIndex;i < candidates.size() && sum + candidates[i] <= target;++i){
            //处理
            sum += candidates[i];
            path.push_back(candidates[i]);
            //递归
            //元素可以重复选择但是为了保证结果集并不重复度，允许选当前值以及其以后的东西，而不允许选择之前的
            backtracking(candidates,target,sum,i);
            //回溯
            sum -= candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        //需要先将candidate排序，不然会出现答案不是顺序出现的情况
        sort(candidates.begin(),candidates.end());
        backtracking(candidates,target,0,0);
        return result;
    }
};

组合总和II

• 思路：

  • 组合里面可能有相同的元素，要对结果进行去重
  • 这个去重指的是同一数层下不可以取相同的元素
  • 也就是说相同的元素只能组成一个组合，但是不可以组成多个组合
  • 用一个bool型数组used，用来记录同一层上的元素是否使用过
    • 如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]

• 注意：

  • 在递归的时候，用的是i+1表示元素不可以重复使用
  • 用i表示元素可以重复使用
  • 不可以用startIndex+1，startIndex只表示这一层从哪里开始，i表示这一层具体遍历到了那个树枝
  • 去重直接使用startIndex去重也是可以的

     if (i > startIndex && candidates[i] == candidates[i -1]){
                continue;
      }
    

• 代码：

class Solution
{
private:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& candidates,int target,int sum,int startIndex,vector<bool>& used){
        //判出条件
        if(sum == target){
            result.push_back(path);
            return;
        }
        //循环
        for(int i = startIndex;i < candidates.size() && sum + candidates[i] <= target; ++i){
            //去重操作，同一层相同的元素只可以被使用一次
            //同一层相等，上一个用过，这一个没用过，跳过
            if(i>0 && candidates[i] == candidates[i-1]&& used[i-1] == false){
                continue;
            }
            sum += candidates[i];
            used[i] = true;
            path.push_back(candidates[i]);
            //递归
            backtracking(candidates,target,sum,i + 1,used);
            //回溯
            used[i] = false;
            sum -= candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        path.clear();
        result.clear();
        vector<bool> used(candidates.size(),false);
        sort(candidates.begin(),candidates.end());
        backtracking(candidates,target,0,0,used);
        return result;
    }
};

分割回文串

• 思路：

  • 遍历举出所有分割好的字符串
  • 判断是不是回文串，如果是的话加入result的集合中
  • 判出条件：
    

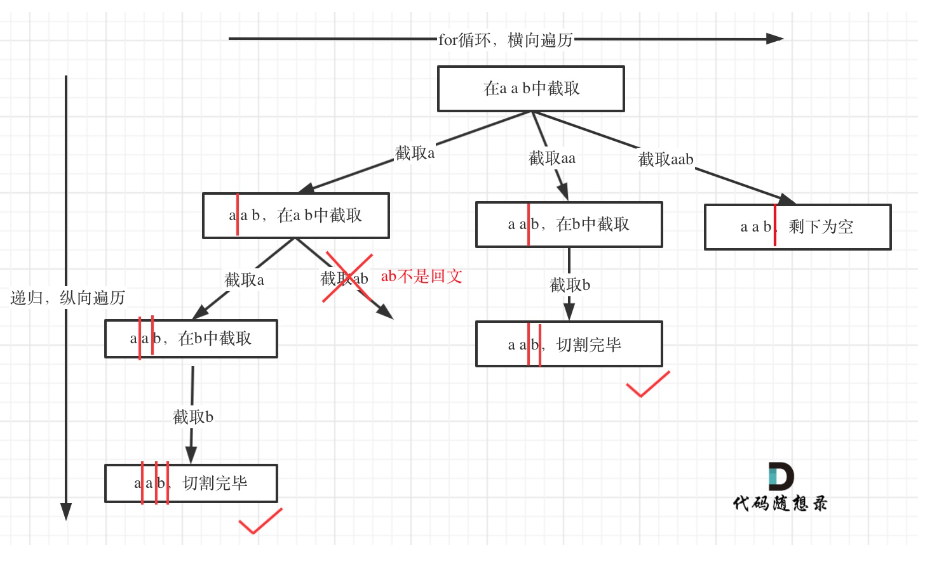
• 注意：

  • 优化：动态规划（待补充）

• 代码：

class Solution
{
private:
    vector<string> path;
    vector<vector<string>> result;
    // 判断是不是回文串用双指针法
    bool isPalindrome(string s, int begin, int end)
    {
        for (int i = begin, j = end; i < j; i++, j--)
        {
            if (s[i] != s[j])
            {
                return false;
            }
        }
        return true;
    }
    // startIndex记录每一层是从哪里开始的，如果startIndex已经到达字符串的最后，证明这一层都遍历完成了
    // 是出口
    void backtracking(string s, int startIndex)
    {
        // 判出条件
        if (startIndex >= s.size())
        {
            result.push_back(path);
            return;
        }
        // 循环遍历每一层
        // 分割线是每次循环时候的i
        for (int i = startIndex; i < s.size(); ++i)
        {
            //处理
            if(isPalindrome(s,startIndex,i)){
                //如果是回文串
                //取出此回文串
                string str = s.substr(startIndex,i - startIndex +1);
                path.push_back(str);
            }else{
                //如果不是回文串的话，直接进入下一个循环
                continue;
            }
            //递归遍历剩下的字符串
            backtracking(s,i+1);
            //回溯
            path.pop_back();
        }
    }

public:
    vector<vector<string>> partition(string s)
    {
        result.clear();
        path.clear();
        backtracking(s,0);
        return result;
    }
};

复原IP地址

• 思路：

  • 分割回文串的加强版

• 注意：

• 代码：

• 思路：

• 注意：

• 代码：

🌈 回溯法总结

• 回溯法抽象为树形之后，遍历过程就是
  • for循环横向遍历
  • 递归纵向遍历
  • 回溯不断调整结果集

贪心算法

🌈 贪心算法理论基础

• 贪心的本质是选择每一阶段的局部最优，从而达到全局最优
• 贪心的套路（什么时候用贪心）
  • 最好的策略就是举反例
• 贪心算法的一般解题步骤分为如下四步：
  • 将问题分解为若干子问题
  • 找出适合的贪心策略
  • 求解每一个子问题的最优解
  • 将局部最优解堆叠成全局最优解

分发饼干

• 思路：

  • 每次都用最大的饼干去满足最大胃口的孩子

• 注意：

  • 注意代码中if条件的判断的顺序

• 代码：

class Solution
{
private:
    
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        //饼干数组的下标
        int index = s.size() - 1;
        int result = 0;
        for(int i = g.size() - 1;i >= 0; i--){
            //如果饼干大于胃口
            if(index >= 0 && s[index] >= g[i]){
                result++;
                index--;
            }
        }
        return result;
    }
};

• 思路：

• 注意：

• 代码：

• 思路：

• 注意：

• 代码：

动态规划

🌈 动态规划理论基础

• DP动态规划的解题步骤
  • 确定dp数组（dp table）以及下标的含义
  • 确定递推公式
  • dp数组如何初始化
  • 确定遍历顺序
  • 举例推导dp数组

斐波那契数

• 思路：

  • 确定dp数组以及下标的含义：第i个数的斐波那契数值是dp[i]
  • 确定递推公式：dp[i] = dp[i - 1] + dp[i - 2]
  • dp数组初始化：dp[0] = 0 dp[1] = 1
  • 确定遍历顺序：dp[i]是依赖dp[i - 1]和dp[i - 2]，那么遍历的顺序一定是从前到后遍历的
  • 举例推导dp数组

• 注意：

• 代码：

class Solution
{
private:
    
public:
    int fib(int n) {
        if(n <= 1) return n;
        vector<int> dp(n + 1);
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2;i <= n;i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};

爬楼梯

• 思路：

• 注意：

  • 分析递推公式的时候看，着眼于当前的方法有多少种
  • 注意递推是从第二个开始的，因此必须大于等于1，需要在开始循环之前增加if判断

• 代码：

class Solution
{
private:
    
public:
    int climbStairs(int n) {
        if(n <= 1){
            return n;
        }
        vector<int> dp(n+1);
        dp[1] = 1;
        dp[2] = 2;
        //dp数组从2开始遍历
        for(int i = 3;i<=n;i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};

使用最小花费爬楼梯

• 思路：

  • 着眼于每一个台阶
  • 一个台阶选择的是一步还是两步，往回推

• 注意：

• 代码：

class Solution
{
private:
    
public:
    int minCostClimbingStairs(vector<int>& cost) {
        //dp数组
        vector<int> dp(cost.size() + 1);
        //初始化，起始台阶选择的时候不需要支付费用
        dp[0] = 0;
        dp[1] = 0;
        //推断到达第二个节点的最小花费
        for(int i = 2;i <= cost.size(); i++){
            dp[i] = min(dp[i - 1] + cost[i - 1],dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.size()];
    }
};

不同路径

• 思路：

  • 用深度优先搜索的时候会超时，上下抽象为两个子树，重点抽象为叶子节点
  • 动态规划
    • 确定dp数组：dp[i][j]表示从(0,0)出发到(i,j)有dp[i][j]条不同的路径
    • 确定递推公式
    • dp数组的初始化
    • 确定遍历顺序，从左到右一层一层的遍历就可以了
    • 举例推导dp数组

• 注意：

• 代码：

class Solution
{
private:
    
public:
    int uniquePaths(int m, int n) {
        //dp[i][j]代表着(0,0)到(i,j)的路径有多少条
        vector<vector<int>> dp(m,vector<int>(n,0));
        //初始化
        //(i,0)都是1，(0,j)都是1，一个方向只有一条
        for(int i = 0;i < m;i++){
            dp[i][0] = 1;
        }
        for(int j = 0;j < n;j++){
            dp[0][j] = 1;
        }
        //遍历
        for(int i = 1;i < m;i++){
            for(int j =1;j < n;j++){
                //当前节点最多的路径只能来自两个方向
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

不同路径II

• 思路：

  • 有障碍就是这个的路径数位0
  • 障碍的初始化为0，其他的初始化为1

• 注意：

  • dp数组初值初始化的时候，如果遇到了障碍，那这个障碍之后的非障碍的路径值也是0

• 代码：

class Solution
{
private:
public:
    int uniquePathsWithObstacles(vector<vector<int>> &obstacleGrid)
    {
        // dp数组
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
         //最开始就应该判断头尾是不是障碍，不能等初始化之后再判断
        if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1)
        {
            return 0;
        }
        vector<vector<int>> dp(m, vector<int>(n, 0));
        // 初始化，非障碍设为1
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++)
        {
                dp[i][0] = 1;
        }
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++)
        {
                dp[0][j] = 1;
        }
        // 遍历
        for (int i = 1; i < m; i++)
        {
            for (int j = 1; j < n; j++)
            {
                // dp公式递推
                if (obstacleGrid[i][j] == 1)
                {
                    continue;
                }
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

整数拆分

• 思路：

  • 拆分之后最大，一定是拆分成了近似相同的数才最大的
  • 用贪心也可以，每次拆分成n个3，如果剩下的是4，则保留4，然后相乘

• 注意：

• 代码：

class Solution
{
private:
    
public:
    int integerBreak(int n) {
        if(n == 2) return 1;
        if(n == 3) return 2;
        if(n == 4) return 4;
        int result = 1;
        while (n > 4){
            result *= 3;
            n -= 3;
        }
        result *= n;
        return result;
    }
};

不同的二叉搜索树

• 思路：

  • 找到dp关系式：关键是看每一步之间的关系
  • dp[i]的含义：1到i为节点组成的二叉搜索树的个数为dp[i]

• 注意：

  • 空结点也是一个二叉搜索树
  • 如果dp[0]为0的话，递推公式就都是0，因此初始化为1

• 代码：

class Solution
{
private:
public:
    int numTrees(int n)
    {
        // 定义dp数组
        vector<int> dp(n + 1);
        // 初始化
        dp[0] = 1;
        // 循环
        for (int i = 1; i <= n; i++)
        {
            // 循环每一个二叉树子树的可能值
            // j从1开始是因为i从1开始的
            for (int j = 1; j <= i; j++)
            {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};

动态规划：01背包理论基础

• 01背包：
  • 问题描述： 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
  • 二维dp数组01背包
    • dp[i][j]表示从下标为[0-i]的物品中任意选取。放进容量为j的背包中，价值总和最大是多少
    • 可以由两个方向去推导出来dp[i][j]：放物品i，不放物品i。
    • dp数组的初始化要根据定义来，如果背包容量为0的话，即dp[i][0]，无论是选取哪些物品，背包总价值一定是0，当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。
    • 递归公式是从左上推导出来的，因此其他下标初始值是什么都没关系，就初始化为0
    • 确定遍历的顺序：有两个遍历的维度，物品和背包重量。两种思路都可以，遍历物品比较好理解

动态规划：01背包理论基础（滚动数组）

• 与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）
• 也就是说上一层的数据是可以重复利用的，那就不用拷贝了，直接用一维数组进行覆盖就可以了
• 一维数组的时候是倒序遍历，因为倒序遍历是为了保证物品i只被放入一次，相当于背包最开始的时候容量是最满的，一点点的往里面加东西。因为对于二维dp，dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖！

分割等和子集

• 思路：

  • 是不是可以分割成两子集元素和相等的元素可以转化成，是不是有元素和为sum/2
  • 用回溯法暴力穷举会超时，选动态规划。每个元素只能用1次，选0/1背包

• 注意：

  • 注意dp数组的下标含义和存储的数据的含义
  • dp数组的下标的含义是背包的容量
  • dp数组内装的是现在背包内的容量
  • 循环递归的时候是一个一个背包遍历往数组里面添加更新的

• 代码：

class Solution
{   
private:
    
public:
    bool canPartition(vector<int>& nums) {
        int n = nums.size();
        //计算素所有的数值的sum
        int sum = 0;
        for(int i = 0;i<n;i++){
            sum+=nums[i];
        }
        if(sum % 2 == 1) return false;
        int m = sum/2;
        //dp数组的下标代表的是背包中的数值数
        //dp数组中存的是当前的value值
        vector<int> dp(10001,0);
        //i代表从第一个物品开始，放不放进去
        for(int i = 0; i < n;i++){
            //递推从后往前开始，当前背包的总容量是m
            //背包容量逐渐减少，直到第一个物品遍历完数组
            //然后开始递归第二个数组，最后dp[m]中存的就是遍历完的总value
            for(int j = m;j>=nums[i];j--){
                //递推公式
                dp[j] = max(dp[j],dp[j - nums[i]]+nums[i]);
            }
        }
        if(dp[m] == m) return true;
        return false;
    }
};

最后一块石头的重量II

• 思路：

  • 可以转化为，尽量将石头分成重量相同的两堆，相撞之后剩下的石头最小。
  • 最平均的就是sum/2

• 注意：

• 代码：

class Solution
{   
private:
    
public:
    int lastStoneWeightII(vector<int>& stones) {
        int n = stones.size();
        int sum  = 0;
        for(int i = 0;i < n;i++){
            sum += stones[i];
        }
        int m = sum/2;
        //定义dp数组
        vector<int> dp(15000,0);
        //循环
        for(int i = 0;i < n;i++){
            //背包最开始的容量是m
            for(int j = m;j >= stones[i];j--){
                //状态方程,加入背包，不加入背包就不变
                dp[j] = max(dp[j],dp[j - stones[i]] + stones[i]);
            }
        }
        return sum - dp[m]*2;
    }
};

目标和

• 思路：

  • 回溯算法会超时，回溯算法的思路补充
  • 动态规划
    • 假设加法的总和为x，那么减法对应的总和就是sum - x
    • 所以我们要求的是 x - (sum - x) = target，x = (target + sum) / 2
    • 此时问题就转化为，装满容量为x的背包，有几种方法

• 注意：

  • x = (target + sum) / 2如果不能整除，那就是没有解
  • 第二层循环的时候，如果背包容量不足现在要加入的nums[i]，那就不应该继续加入

• 代码：

class Solution
{   
private:
    
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        //将求target转化成求(sum+target)/2
        int sum = 0;
        for(int i = 0;i < nums.size();i++){
            sum += nums[i];
        }
        int x = (sum + target)/2;
        ///排除掉没有结果的答案
        if(abs(target) > sum) return 0;
        if((sum + target)%2 == 1) return 0;
        //背包,dp数组的含义：容量为j的背包里面最多放多少东西
        //初始化
        vector<int> dp(x + 1,0);
        //如果和为0的话，证明一半一半，只有1种可能
        dp[0] = 1;
        //循环
        for(int i = 0;i < nums.size();i++){
            for(int j = x; j >= nums[i];j--){
                //递推公式
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[(sum+target)/2];
    }
};

一和零

• 思路：

  • 由于每个物品只能选择一次，因此是01背包
  • 由于是两个因素的背包，因此是二维背包

• 注意：

  • 二维背包和一维背包用二维数组是不一样的
    • 二维背包要两层都从后往前遍历
    • 一维背包用二维数组，第一层物品可以从前往后遍历，第二层背包需要从后往前遍历，可以改用动态数组。

• 代码：

class Solution
{   
private:
    
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        //二维dp数组
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        //strs字符串数组中的字符串相当于是物品，01数量相当于容量
        for(string str : strs){
            int oneNum = 0, zeroNum = 0;
            //开始计算是不是将当前的物品放进去
            for(char c : str){
                if(c == '0') zeroNum++;
                else oneNum++;
            }
            //遍历背包且从后向前遍历
            //m是0的个数，n是1的个数
            for(int i = m;i>=zeroNum;i--){
                for(int j = n;j>=oneNum;j--){
                    dp[i][j] = max(dp[i][j],dp[i-zeroNum][j - oneNum]+1);
                }
            }
        }
        return dp[m][n];
    }
};

动态规划：完全背包理论基础

• 完全背包：有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大
  • 完全背包和01背包问题唯一不同的地方就是，每种物品有无限件
  • 在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！

零钱兑换II

• 思路：

  • 无限多个硬币可以选择用完全背包
  • 纯完全背包是凑出总和，本题的是求组合数（不是排序数），需要去重
  • 先遍历钱币再遍历背包：求出的是组合数
  • 先遍历背包再遍历钱币：求出的是排序数

• 注意：

  • 第二层递推表达式

• 代码：

class Solution
{   
private:
    
public:
    int change(int amount, vector<int>& coins) {
        //定义dp数组
        vector<int> dp(amount+1,0);
        //初始化dp数组，如果第一个值为0，后面推导出来的所有值都为0，就没有意义了
        dp[0] = 1;
        //求组合数，先遍历硬币
        for(int i = 0;i < coins.size();i++){
            for(int j = coins[i];j<=amount;j++){
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
};

组合总和 Ⅳ

• 思路：

  • 本题主要是求组合的个数，如果本题要把排列都列出来的话，只能使用回溯算法爆搜

• 注意：

  • 本题求的是排列，应该先遍历容量再遍历物品

• 代码：

class Solution
{   
private:
    
public:
    int combinationSum4(vector<int>& nums, int target) {
        //dp数组
        vector<int> dp(target+1,0);
        //初始化
        dp[0] = 1;
        //求的是排列数
        for(int i = 0;i<=target;i++){
            for(int j = 0;j < nums.size();j++){
                //如果这个数值可以放进这个背包
                if(i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]]){
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
};

爬楼梯（进阶版）

• 思路：

  • 转化成背包容是楼梯的总数量，物品价值为1/2，物品可以无限量的选取的完全背包 问题
  • dp[i] 爬到有i个台阶的楼梯，有dp[i]种方法

• 注意：

• 代码：

零钱兑换

• 思路：

  • 要求最小的硬币的个数，状态方程是最小的

• 注意：

• 代码：

class Solution
{   
private:
    
public:
    int coinChange(vector<int>& coins, int amount) {
        //dp数组
        //这个时候求的是最小值，所以定义的是最大值
        vector<int> dp(amount+1, INT_MAX);
        //初始化
        dp[0] = 0;
        //循环，滚动数组
        for(int i = 0;i < coins.size();i++){
            for(int j = coins[i];j<=amount;j++){
                //如果是初始值则跳过
                if(dp[j - coins[i]] != INT_MAX){
                    dp[j] = min(dp[j - coins[i]]+1,dp[j]);
                }
            }
        }
        if(dp[amount] == INT_MAX) return -1;
        return dp[amount];
    }
};

完全平方数

• 思路：

  • 完全平方数相当于物品
  • 凑正整数n相当于背包

• 注意：

• 代码：

class Solution
{   
private:
    
public:
    int numSquares(int n) {
        //dp数组
        vector<int> dp(n+1,INT_MAX);
        //初始化
        dp[0] = 0;
        //遍历背包
        for(int i  = 0;i <= n;i++){
            //遍历物品
            for(int j = 1; j*j <= i;j++){
                    dp[i] = min(dp[i - j*j]+1,dp[i]);
            }
        }
        if(dp[n] == INT_MAX) return 0;
        return dp[n];
    }
};

单词拆分

• 思路：

  • 动态规划：字典中的单词相当于物品，背包相当于s，可以多次选择是完全背包，选择的时候不同顺序是不同的，排序背包在外，物品在里
  • 回溯算法：暴力枚举多有的字符串的分割情况，可以用记忆化数组进行优化
    • 回溯算法会超时
    • 记忆化递归 递归的过程中有很多重复计算，可以用数组保存一下递归过程中计算的结果

• 回溯法未优化的代码

class Solution {
private:
    bool backtracking (const string& s, const unordered_set<string>& wordSet, int startIndex) {
        if (startIndex >= s.size()) {
            return true;
        }
        for (int i = startIndex; i < s.size(); i++) {
            string word = s.substr(startIndex, i - startIndex + 1);
            if (wordSet.find(word) != wordSet.end() && backtracking(s, wordSet, i + 1)) {
                return true;
            }
        }
        return false;
    }
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
        return backtracking(s, wordSet, 0);
    }
};

• 回溯法已优化的代码（有时间补充）

• 背包问题

  • 拆分的时候可以重复使用字典中的单词，说明是完全背包
  • 求得是排列数而不是组合数，先遍历背包再遍历物品

• 注意：

• 代码：

class Solution {
private:

public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(),wordDict.end());
        vector<bool> dp(s.size() + 1,false);
        dp[0] = true;
        //遍历背包
        for(int i = 1;i <= s.size();i++){
            //遍历物品
            for(int j = 0;j<i;j++){
                string word = s.substr(j,i-j);
                if(wordSet.find(word) != wordSet.end() && dp[j]){
                    dp[i] = true;
                }
            }
        }
        return dp[s.size()];
    }
};

多重背包理论基础

• 多重背包同一价值物品有多件可以使用，把多件进行摊开，类似于01背包

• 思路：

• 注意：

• 代码：

打家劫舍

• 思路：

• 注意：

• 代码：

class Solution
{
private:
    
public:
    int rob(vector<int>& nums) {
        if(nums.size() == 0) return 0;
        if(nums.size() == 1) return nums[0];
        vector<int> dp(nums.size());
        //初始化
        dp[0] = nums[0];
        dp[1] = max(nums[0],nums[1]);
        //遍历
        for(int i = 2;i < nums.size();i++){
            //递推式
            dp[i] = max(dp[i-1],dp[i-2] + nums[i]);
        }
        return dp[nums.size() - 1];
    }
};

打家劫舍II

• 思路：

  • 这里面成环了
  • 首尾元素只考虑一个就可以了，因为选了首元素就不可能选择尾元素，选择尾元素就不可能选择首元素

• 注意：

• 代码：

class Solution
{
private:
    
public:
    //标准的打家劫舍，然后进行抽离
    int robRange(vector<int>& nums,int begin,int end) {
        if(begin == end) return nums[begin];
        if(end - begin == 1) return max(nums[begin],nums[end]);
        vector<int> dp(nums.size());
        //初始化
        dp[begin] = nums[begin];
        dp[begin + 1] = max(nums[begin],nums[begin + 1]);
        //循环
        for(int i = begin + 2; i <= end; i++){
            dp[i] = max(dp[i-1],dp[i-2]+nums[i]);
        }
        return dp[end];
    }
    int rob(vector<int>& nums) {
        //考虑选头和考虑选尾两种情况
        if(nums.size() == 0) return 0;
        if(nums.size() == 1) return nums[0];
        int head = robRange(nums,0,nums.size()-2);
        int end = robRange(nums,1,nums.size() - 1);
        return max(head,end);
    }
};

• 思路：

• 注意：

• 代码：

• 思路：

• 注意：

• 代码：

单调栈

• 思路：

• 注意：

• 代码：

图论

深度优先搜索理论基础

• dfs和bfs的区别
  • dfs是可一个方向去搜索，然后回溯
  • bfs是把本节点所有的节点都遍历一遍
• dfs
  • 代码框架
  • 深搜三部曲
    • 确认递归函数，参数
    • 确认终止条件
    • 处理目前搜索节点出发的路径

void dfs(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

所有可能的路径

• 思路：

• 注意：

• 代码：

class Solution
{
private:
    //收集符合条件的路径
    vector<vector<int>> result;
    //收集0节点到终点的路径
    vector<int> path;
    //x代表的是目前遍历的节点
    //graph代表的是边
    void dfs(vector<vector<int>>& graph,int x){
        //判出条件
        //当遍历的节点来到了最后一个节点，输出
        if(x == graph.size() - 1){
            result.push_back(path);
            return;
        }
        //回溯
        //for代表同一层内有多少个节点可以供选择
        for(int i = 0;i < graph[x].size();i++){
            path.push_back(graph[x][i]);
            dfs(graph,graph[x][i]);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        //无论什么路径都是从0节点出发
        path.push_back(0);
        //开始遍历
        dfs(graph,0);
        return result;
    }
};

广度优先搜索理论基础

• bfs的使用场景

  • 解决两个点之间的最短路径问题
  • 岛屿问题不涉及具体的遍历方式，只要能把相邻且相同属性的节点标记上就行

• 广度优先搜索的代码模板

  • 广度有限搜索用队列或者用栈都是可以的
  • 用队列的话就是往同一个方向去转
  • 用栈的话就是第一圈顺时针，第二圈逆时针，因为栈是后进先出

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图，也就是一个二维数组
// visited标记访问过的节点，不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
    queue<pair<int, int>> que; // 定义队列
    que.push({x, y}); // 起始节点加入队列
    visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
    while(!que.empty()) { // 开始遍历队列里的元素
        pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
        int curx = cur.first;
        int cury = cur.second; // 当前节点坐标
        for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过
            if (!visited[nextx][nexty]) { // 如果节点没被访问过
                que.push({nextx, nexty});  // 队列添加该节点为下一轮要遍历的节点
                visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
            }
        }
    }
}

岛屿数量（深搜版）

• 思路：

  • 用遇到一个没有遍历过的节点陆地，计数器就加一，然后把该节点陆地所能遍历到的陆地都标记上
  • 在遇到标记过的陆地节点和海洋节点的时候直接跳过。

• 注意：

• 代码：

class Solution
{
private:
    //代表方向的意思
    int dir[4][2] = {0,1,1,0,-1,0,0,-1};
    //dfs的目的是标记所有和其相连的陆地
    //传入的参数是处理的当前的节点和原数组和原数组的使用情况
    void dfs(vector<vector<char>>& grid,vector<vector<bool>>& used,int x,int y){
        //判出条件
        if(used[x][y] || grid[x][y] == '0'){
            return;
        }
        used[x][y] = true;
        //递归，遍历四个方向
        for(int i = 0;i < 4;i++){
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            //判断是否越界
            if(nextx < 0|| nextx >= grid.size()||nexty < 0 || nexty >= grid[0].size()){
                continue;
            }
            dfs(grid,used,nextx,nexty);
        }
    }
public:
    int numIslands(vector<vector<char>>& grid){
        int n = grid.size();
        int m = grid[0].size();

        vector<vector<bool>> used = vector<vector<bool>>(n,vector<bool>(m,false));
        int num = 0;
        for(int i = 0;i<n;i++){
            for(int j = 0;j < m;j++){
                if(!used[i][j] && grid[i][j] == '1'){
                    num++;
                    dfs(grid,used,i,j);
                }
            }
        }
        return num;
    }
};

岛屿数量（广搜版）

• 思路：

• 注意：

• 代码：

岛屿的最大面积

• 思路：

  • 普通的dfs题目

• 注意：

• 代码：

class Solution
{
private:
    int count;
    int dir[4][2] = {0,1,1,0,-1,0,0,-1};
    void dfs(vector<vector<int>>& grid,vector<vector<bool>>& used,int x,int y){
        //判出条件
        if(used[x][y] || grid[x][y] == 0){
            return;
        }
        //处理
        used[x][y] = true;
        count++;
        //递归
        for(int i = 0;i < 4; ++i){
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            //边界处理
            if(nextx<0||nextx>=grid.size()||nexty<0||nexty>=grid[0].size()){
                continue;
            }
            dfs(grid,used,nextx,nexty);
        }
    }
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int result = 0;
        int n = grid.size();
        int m = grid[0].size();
        vector<vector<bool>> used = vector<vector<bool>>(n,vector<bool>(m,false));
        //遍历
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                if(!used[i][j] && grid[i][j] == 1){
                    count = 0;
                    dfs(grid,used,i,j);
                    result = max(result,count);
                }
            }
        }
        return result;
    }
};

飞地的数量

• 思路：

  • 从周边进入，讲所有的陆地都变成海洋
  • 重新遍历，统计所有的陆地数

• 注意：

• 代码：

class Solution
{
private:
    int dir[4][2] = {-1, 0, 0, -1, 0, 1, 1, 0};
    int count;
    void dfs(vector<vector<int>> &grid, int x, int y)
    {
        // 将遍历过的陆地都变成海洋
        grid[x][y] = 0;
        count++;
        for (int i = 0; i < 4; i++)
        {
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            // 判断边界
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size())
                continue;
            if (grid[nextx][nexty] == 0)
                continue;
            dfs(grid, nextx, nexty);
        }
        return;
    }

public:
    int numEnclaves(vector<vector<int>> &grid)
    {
        int m = grid.size();
        int n = grid[0].size();
        // 上和下，x值固定
        for (int i = 0; i < n; i++)
        {
            if (grid[0][i] == 1)
                dfs(grid, 0, i);
            if (grid[m - 1][i] == 1)
                dfs(grid, m - 1, i);
        }
        // 左和右，y值固定
        for (int i = 0; i < m; i++)
        {
            if (grid[i][0] == 1)
                dfs(grid, i, 0);
            if (grid[i][n - 1] == 1)
                dfs(grid, i, n - 1);
        }
        count = 0;
        for(int i = 0;i<m;i++){
            for(int j = 0;j<n;j++){
                if(grid[i][j] == 1) dfs(grid,i,j);
            }
        }
        return count;
    }
};

被围绕的区域

• 思路：

  • 节约空间，直接把符合的数据改成其他的值

• 注意：

• 代码：

class Solution
{   
private:
    int dir[4][2] = {-1,0,0,-1,1,0,0,1};
    void dfs(vector<vector<char>>& board,int x,int y){
        board[x][y] = 'A';
        for(int i = 0;i<4;i++){
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            //判断边界
            if(nextx < 0 || nextx >= board.size() || nexty < 0 || nexty >= board[0].size()) continue;
            //处理
            if(board[nextx][nexty] == 'X' || board[nextx][nexty] == 'A') continue;
            dfs(board,nextx,nexty);
        }
        return;
    }
public:
    void solve(vector<vector<char>>& board) {
        int m = board.size();
        int n = board[0].size();
        for(int i = 0;i < m;i++){
            if(board[i][0] == 'O') dfs(board,i,0);
            if(board[i][n-1] == 'O') dfs(board,i,n-1);
        }
        for(int i = 0;i < n;i++){
            if(board[0][i] == 'O') dfs(board,0,i);
            if(board[m-1][i] == 'O') dfs(board,m-1,i);
        }
        for(int i = 0;i<m;i++){
            for(int j = 0;j<n;j++){
                if(board[i][j] == 'O') board[i][j] = 'X';
                if(board[i][j] == 'A') board[i][j] = 'O';
            }
        }
    }
};

太平洋大西洋水流问题

• 思路：

• 注意：

• 代码：