7D

D. Palindrome Degree

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

String s of length n is called k-palindrome, if it is a palindrome itself, and its prefix and suffix of length 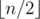 are (k - 1)-palindromes. By definition, any string (even empty) is 0-palindrome.

Let's call the palindrome degree of string s such a maximum number k, for which s is k-palindrome. For example, "abaaba" has degree equals to 3.

You are given a string. Your task is to find the sum of the palindrome degrees of all its prefixes.

Input

The first line of the input data contains a non-empty string, consisting of Latin letters and digits. The length of the string does not exceed 5·106. The string is case-sensitive.

Output

Output the only number — the sum of the polindrome degrees of all the string's prefixes.

Sample test(s)

input

a2A

output

1

input

abacaba

output

6

 

 

#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<climits>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<stack>
#include<set>
#include<map>
#define INF 0x3f3f3f3f
using namespace std;

const int MAXN=5100000;
char s[MAXN<<1];
int p[MAXN<<1];
int rank[MAXN];

int main()
{
    while(~scanf("%s",s))
    {
        int n=strlen(s);
        s[2*n+2]='\0';
        for(int i=n-1; i>=0; i--)
        {
            s[2*i+2]=s[i];
            s[2*i+3]='*';
        }
        s[0]='$';
        s[1]='*';
        memset(p,0,sizeof(p));
        int maxn=0,maxi=0;
        long long ans=0LL;
        for(int i=1; i<2*n+2; i++)
        {
            p[i]=maxn>i?min(p[2*maxi-i],maxn-i):1;
            while(s[i+p[i]]==s[i-p[i]])p[i]++;
            if(maxn<i+p[i])
            {
                maxn=i+p[i];
                maxi=i;
            }
        }
        memset(rank,0,sizeof(rank));
        for(int i=0; i<n; i++)
        {
            if(p[i+2]!=i+2)
            {
                rank[i]=0;
            }
            else
            {
                if(i)
                {
                    rank[i]=rank[(i-1)/2]+1;
                }
                rank[i]=max(rank[i],1);
            }
            ans+=rank[i];
        }
        printf("%I64d\n",ans);
    }
    return 0;
}

　　不好想( ╯□╰ )，用macacher 算法，判断p[i]是否为i，若想等说明是回文，i为中心，更新 rank[i]=rank[(i-1)/2]+1;