(搜索)cf 486D

D. Valid Sets

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As you know, an undirected connected graph with n nodes and n - 1 edges is called a tree. You are given an integer d and a tree consisting of n nodes. Each node i has a value ai associated with it.

We call a set S of tree nodes valid if following conditions are satisfied:

1. S is non-empty.
2. S is connected. In other words, if nodes u and v are in S, then all nodes lying on the simple path between u and v should also be presented in S.
3. .

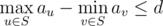Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo 1000000007 (109 + 7).

Input

The first line contains two space-separated integers d (0 ≤ d ≤ 2000) and n (1 ≤ n ≤ 2000).

The second line contains n space-separated positive integers a1, a2, ..., an(1 ≤ ai ≤ 2000).

Then the next n - 1 line each contain pair of integers u and v (1 ≤ u, v ≤ n) denoting that there is an edge between u and v. It is guaranteed that these edges form a tree.

Output

Print the number of valid sets modulo 1000000007.

Sample test(s)

input

1 4
2 1 3 2
1 2
1 3
3 4

output

8

input

0 3
1 2 3
1 2
2 3

output

3

input

4 8
7 8 7 5 4 6 4 10
1 6
1 2
5 8
1 3
3 5
6 7
3 4

output

41

Note

In the first sample, there are exactly 8 valid sets: {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {3, 4} and {1, 3, 4}. Set {1, 2, 3, 4} is not valid, because the third condition isn't satisfied. Set {1, 4} satisfies the third condition, but conflicts with the second condition.

 

 

#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;

typedef long long ll;
const ll mod = 1e9 + 7;
const int maxn = 2005;

int N, D, W[maxn];
vector<int> G[maxn];

ll dfs(int u, int f, int rt) {
    int n = G[u].size();
    ll ret = 1;

    for (int i = 0; i < n; i++) {
        int v = G[u][i];

        if (v == f || W[rt] < W[v] || (W[rt] == W[v] && v > rt) || W[rt] - W[v] > D)
            continue;
        ret = ret * (dfs(v, u, rt) + 1) % mod;
    }
    return ret;
}

int main () {
    scanf("%d%d", &D, &N);
    for (int i = 1; i <= N; i++)
        scanf("%d", &W[i]);
    int u, v;
    for (int i = 1; i < N; i++) {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
    }

    ll ans = 0;
    for (int i = 1; i <= N; i++)
        ans = (ans + dfs(i, -1, i)) % mod;
    printf("%lld\n", ans);
    return 0;
}