决策树算法
决策树算法历史：
简单实例：
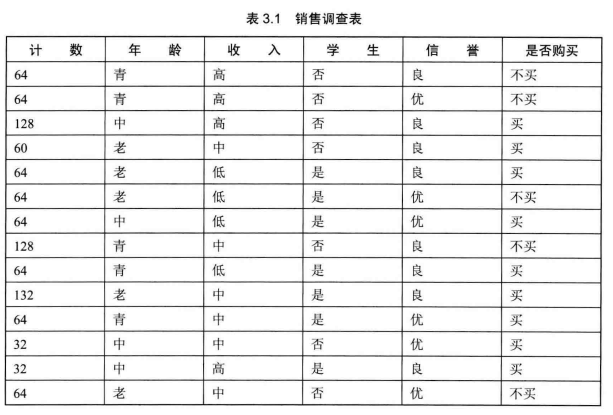
Q1:如何对客户分类？
Q2:如何根据分类的依据，对销售人员给出销售意见？
已该种方式选取各节点产生树形图：(怎么选取节点会更优？)
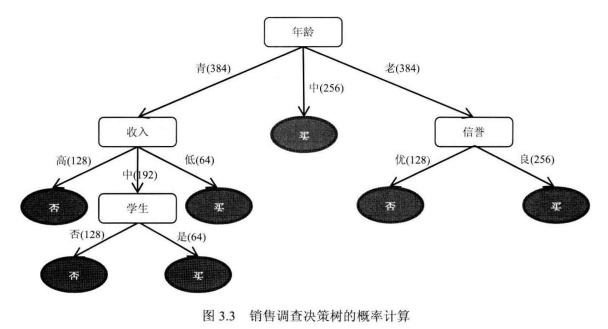
二、决策树算法框架
1、决策树主函数
各种决策树主函数都大同小异，本质上是一个递归函数。其主要有如下几个功能：
- 1、输入需要分类的数据集合类别标签
- 2、根据某种分类规则得到最优的划分特征，并创建特征的划分节点--计算最优特征子函数。
- 3、按照该特征的每个取值划分数据集为若干部分--划分数据集子函数
- 4、根据划分子函数的计算结果构建出新的节点，作为数生长出新的分支
- 5、检验是否符合递归的终止条件
- 6、将划分的新节点包含的数据集和类别标签作为输入，递归执行上述步骤
2、计算最优特征子函数
计算最优特征子函数是除主函数外最重要的函数，构建的决策树不同，一般是因为最优特征标准有差异，例如 ID3的最优特征选择标准是信息增益、C4.5是信息增益率、CART是节点方差的大小
在算法逻辑上，一般选择最优特征要遍历整个数据集，评估每个特征，返回最优特征。
3、划分数据集
4、分类器
决策树的分类器基石通过遍历整个决策树，找到测试集中叶子节点对应的类别标签
5、信息熵测度
一般在数据集中经常有一些定型的字符串数据，也就是标称数据，直接只用这些数据会使得算法缺乏泛化能力，在实际计算中需要定量化为数字，也就是离散化。
通常一个信源发出时什么事件是不确定的，可以根据其出现的概率来度量。概率越大，发生的机会就越大，不确定性小；反之不确定就大。 # 单调递减性质，事件独立要可加
不确定性函数 I 就称为事件的信息量，是事件U发生概率p的单调递减函数；两个独立事件所产生的不确定性等于各不确定性之和，即 I(p1,p2) = I(p1) + I(p2),
这称为可加性，同时满足这两个条件的函数 I 是对数函数。
I(U) = Log(1/p) = -Log(p) # 满足单调递减可加
在一个信源(数据集)中，要考虑所有信源可能情况的不确定性。假设信源有n中情况，对应发生的概率也有n种，且各事件独立，信源的平均不确定性为各事件不确定性的平均值
，可称为信息熵。
H(U) = E[-Log(p_i)]
在决策树中，信息熵可以用来度量包含不同特征(多列)的数据样本与类别(标签)的不确定性，即某个特征列向量的信息熵越大，说明该向量的不确定性程度越大，即混乱程度越大
，就应该优先从该向量着手进行划分。信息熵为决策树的划分提供了最重要的依据和标准。
假设数据集S有s个样本，m 个标签类别，s_m对应某个标签类别数据集个数，
某类标签的信息熵如下式：
I(s_m) = -p_i * Log_2(p_i) # 计算整个数据集的信息熵
p_i是某类标签对应样本发生的概率，p_i = s_i / S -- S属于样本总数
然后计算每个特征列的信息熵：以上述数据为例，计算 “年龄” 的信息熵
先将年龄分为三类，青年；中年；老年，计算出各类年龄段的 买或不买的数量，以青年年龄段为例，计算出青年买的数量 S(青年/买) ，S(青年/不买)
P(青年/买) = S(青年/买) / S(青年/总)， P(青年/不买) = S(青年/不买) / S(青年/总)
青年对应的信息增益为：I(青年) = --P(青年/买) * log2(P(青年/买))
同样方法算出其他年龄段的信息熵， I(中年)， I(老年)，特征年龄的信息熵为各年龄段平均信息熵(信息熵的可加性)， E(年龄) = (I(青年) + I(中年) + I(老年)) / 3
然后计算出该特征的信息增益，他是确定决策树分支的划分依据，是决策树某个分支上整个数据集信息熵与当前节点信息熵的差值：
Gain(A) =I(s1, s2..s_m) -- E(A)
具有最高信息增益的特征可选做给定集合 S 的测试属性
根据上述同样方法算出其他特征列的信息增益
