软工个人项目博客
软工个人项目作业
教学班级:005(周三上午三四节)
项目地址:https://github.com/a458269373/software_first
PSP2.1表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 100 | 150 |
| · Design Spec | · 生成设计文档 | 50 | 60 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 15 | 15 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 15 | 15 |
| · Design | · 具体设计 | 60 | 80 |
| · Coding | · 具体编码 | 30 | 30 |
| · Code Review | · 代码复审 | 40 | 40 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 200 | 250 |
| Reporting | 报告 | 100 | 100 |
| · Test Report | · 测试报告 | 30 | 30 |
| · Size Measurement | · 计算工作量 | 20 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 50 | 60 |
| - | 合计 | 720 | 860 |
解题思路
本次作业只完成了求直线交点部分:
直线方程使用\(ax+by+c=0\)的形式,可以很好的规避斜率问题,进而减少分类讨论。
可以很容易的得到,直线给出两点\((x1,y1)、(x2,y2)\),则直线方程中的参数可以表示为:
\(\begin{cases} a = y1-y2\\ b = x1 - x2\\c = y2 * x1 - y1 * x2\end{cases}\)
求两直线相交时,直线方程为\(a1x+b1y+c1=0\)、\(a2x+b2y+c2=0\),根据公式推导可得:
\(\begin{cases} x = (b1 * c2 - b2 * c1)/(a1 * b2 - a2 *b1)\\ y = (a2 *c1 - a1 * c2 )/(a1 * b2 - a2 *b1)\\\end{cases}\)
最终,去重后交点个数即为所求。
实现思路与实现结构
本次作业我使用了两种思路:
第一种思路:两点确定一条直线,每次读入一条直线,将已求出的交点代入新读入的直线中,情况有以下几种:
1、有两个点及以上在新直线上,则新直线必于之前读入的某条直线重合,所以可以直接放弃新直线。
2、只有一点在新直线上,则找到经过该点的所有直线,新直线与这些直线不会产生新的交点,省去了一批重复运算。
3、无交点在新直线上,则新直线计算与全部已有直线的焦点。
性能改进:通过查阅资料了解到,直线求交点问题无法逃出遍历的牢笼,只能在去重这一点上做出优化。
具体实现:
struct point {
double x; // 横坐标
double y;//纵坐标
vector<int> belong;//直线下标
};
class line {
public:
//ax+by+c=0
long long a = 0;
long long b = 0;
long long c = 0;
static void calInteract(line l1, line l2);
line(long long x1, long long y1, long long x2, long long y2);
};
//main 逻辑
line templine(x1, y1, x2, y2);
if(addInteract(templine,lineNum) < 2){
//只有小于2,新直线才不重合
for (int j = 0; j < lineNum; j++) {
if(find(InteractLine.begin(),InteractLine.end() == InteractLine.begin()){
//去重逻辑,两直线不相交于已计入的焦点。
line::calInteract(templine, lines[j]);
}
}
lines.push_back(templine);
lineNum++;
}
一个类line,一个结构体point。
第二种思路:暴力运算,每条直线实现简单的相交运算:
使用pair<double,double>来表示每一个点,使用map的key的不可重复性来去重。
具体实现过程:
vector<line> lines;
map<pair<double, double>,int> points;
class line {
public:
//ax+by+c=0
long long a = 0;
long long b = 0;
long long c = 0;
static void calInteract(line l1, line l2);
line(long long x1, long long y1, long long x2, long long y2);
};
//关键函数逻辑:
//使用公式代入
long long temp = a1 * b2 - a2 * b1;
pair<double,double> ans;
if (temp != 0) {
x = (1.0 * (c2 * b1 - c1 * b2)) / (1.0 * temp);
y = (1.0 * (a2 * c1 - a1 * c2)) / (1.0 * temp);
ans = pair<double, double>(double(x), double(y));
points.insert(pair<pair<double, double>, int>(ans, 1));
}
改进程序性能的过程
最初我使用了第一种实现思路,但是发现没有办法很好地实现浮点数部分的去重,所以我使用了第二种实现策略,第二种实现策略的好处在于,map自身集成了去重的功能,所以可以很好的利用这一点,达到一个简化代码提高效率的目的。
当测试数据为2000条数据时,性能测试如下:
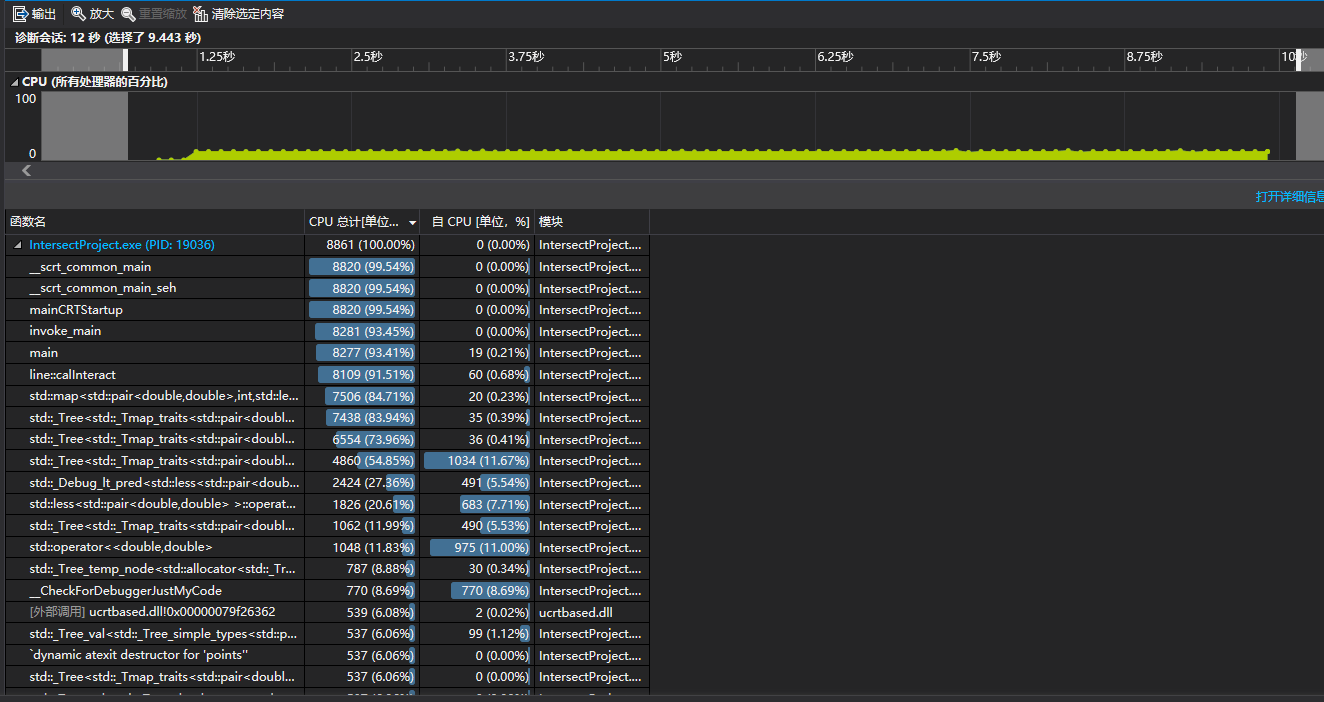
调用细节如下:
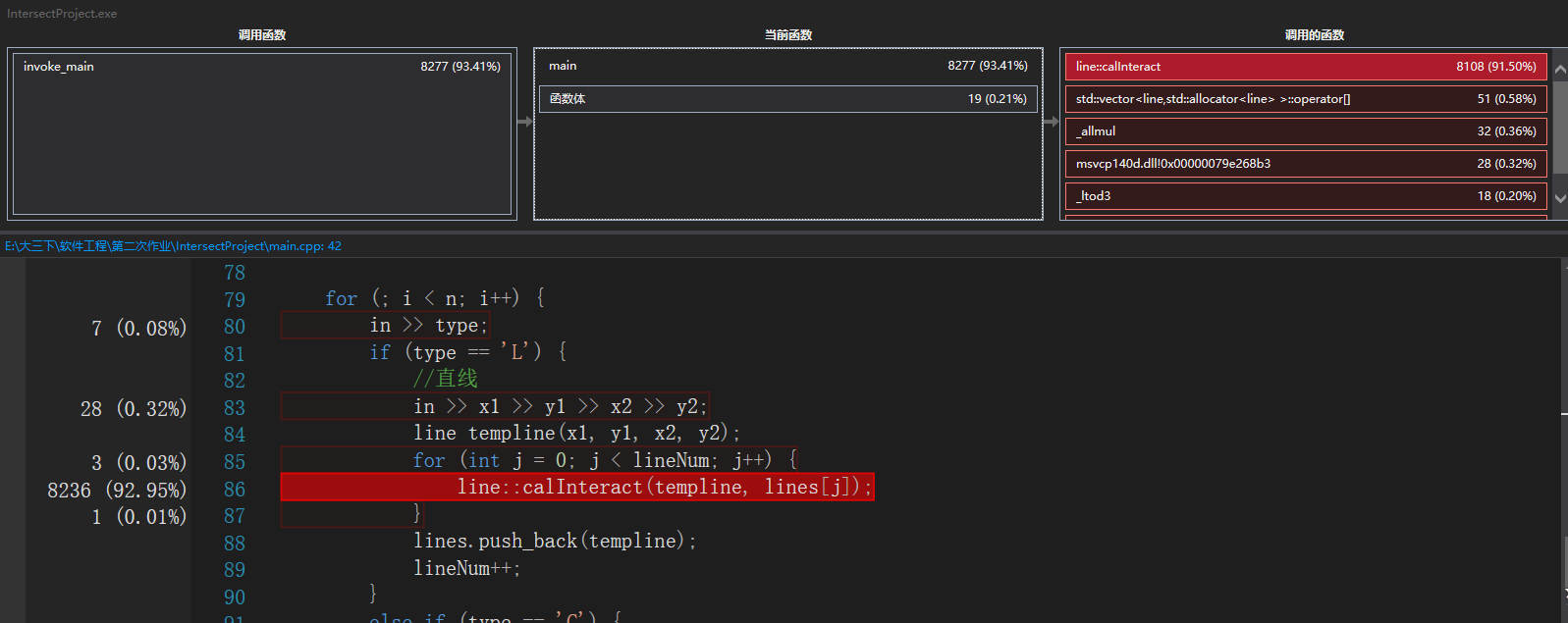
可以看到具体调用最为频繁的是核心算法,计算相交直线的部分。
代码说明
直线交点计算部分,为了简化斜率的讨论,直接采用了直线方程的一般式(\(ax+by+c=0\)):

代码管理部分:
消除warning:

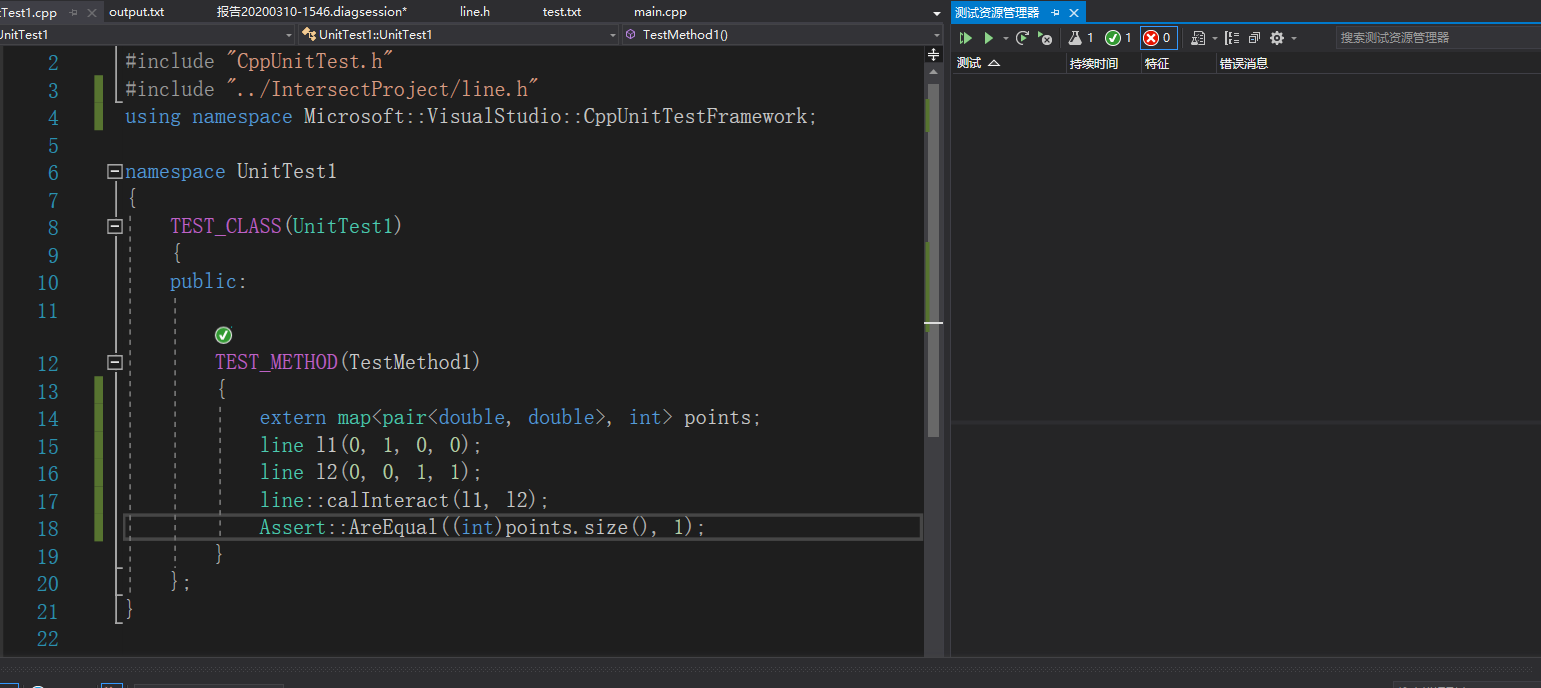
单元测试: