Educational Codeforces Round 41 (Rated for Div. 2)D. Pair Of Lines

D. Pair Of Lines

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given n points on Cartesian plane. Every point is a lattice point (i. e. both of its coordinates are integers), and all points are distinct.

You may draw two straight lines (not necessarily distinct). Is it possible to do this in such a way that every point lies on at least one of these lines?

Input

The first line contains one integer n (1 ≤ n ≤ 10⁵) — the number of points you are given.

Then n lines follow, each line containing two integers x_i and y_i (|x_i|, |y_i| ≤ 10⁹)— coordinates of i-th point. All n points are distinct.

Output

If it is possible to draw two straight lines in such a way that each of given points belongs to at least one of these lines, print YES. Otherwise, print NO.

Examples

Input

Copy

5
0 0
0 1
1 1
1 -1
2 2

Output

Copy

YES

Input

Copy

5
0 0
1 0
2 1
1 1
2 3

Output

Copy

NO

Note

In the first example it is possible to draw two lines, the one containing the points 1, 3 and 5, and another one containing two remaining points.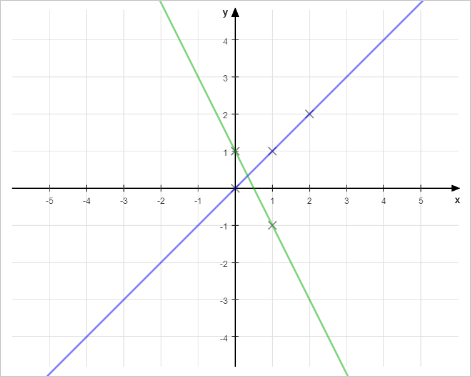

题意 给出n个点的横纵坐标，问能否用两条直线覆盖所有的点

分析： 如果是5个点以下，则一定可以用两条直线表示

            当为5个点及以上时候，先选出5个点，如果成立的话，则在其中一定有三个点共线，确立了第一条直线。

            这时候找出共线的这三个点，枚举其他的点，如果出现与这三个点不共线的两个点之后，将这两个点看作另一条直线。

            随后继续枚举其他的点，如果出现不在这两条直线上的点，则一定不成立。

 

代码如下：

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
const int MAXN=1e5+100;
typedef long long LL;
struct node
{
    LL x;
    LL y;
}poi[MAXN];
bool check(node a,node b,node c)
{
   if((a.y-b.y)*(b.x-c.x)==(b.y-c.y)*(a.x-b.x))
    return true;
   return false;
}
int n;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    scanf("%lld%lld",&poi[i].x,&poi[i].y);
    if(n<=4)
     puts("YES");
    else
    {
      int flag=0;
      int a,b,c,d,e,tel;
      d=-1,e=-1;
      for(int i=1;i<=5;i++)
        for(int j=1;j<=5;j++)
      {
          if(j==i)continue;
          for(int k=1;k<=5;k++)
          {
              if(k==j||k==i)continue;
              if(check(poi[i],poi[j],poi[k]))
              {
                 flag=1;
                 a=i;
                 b=j;
                 c=k;
                 break;
              }
          }
      }

      if(flag==0)
      puts("NO");
      else
      {
          for(int i=1;i<=n;i++)
          {
             if(i==a||i==b||i==c)
              continue;
             if(!check(poi[a],poi[b],poi[i]))
             {
                 if(d==-1)
                 d=i;
                 else
                 {
                   e=i;
                   tel=i+1;
                   break;
                 }
             }
          }
          if(d==-1||e==-1)
           puts("YES");
          else
          {
             int flag2=1;
             for(int i=tel;i<=n;i++)
             {
                if(!check(poi[a],poi[b],poi[i])&&!check(poi[d],poi[e],poi[i]))
                {
                    flag2=0;
                    break;
                }
             }
             if(flag2==1)puts("YES");
             else puts("NO");
          }

      }
    }

    return 0;
}