codeforce 932E Team Work(第二类斯特林数）

E. Team Work

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You have a team of N people. For a particular task, you can pick any non-empty subset of people. The cost of having x people for the task is x^k.

Output the sum of costs over all non-empty subsets of people.

Input

Only line of input contains two integers N (1 ≤ N ≤ 10⁹) representing total number of people and k (1 ≤ k ≤ 5000).

Output

Output the sum of costs for all non empty subsets modulo 10⁹ + 7.

Examples

Input

Copy

1 1

Output

1

Input

Copy

3 2

Output

24

Note

In the first example, there is only one non-empty subset {1} with cost 1¹ = 1.

In the second example, there are seven non-empty subsets.

- {1} with cost 1² = 1

- {2} with cost 1² = 1

- {1, 2} with cost 2² = 4

- {3} with cost 1² = 1

- {1, 3} with cost 2² = 4

- {2, 3} with cost 2² = 4

- {1, 2, 3} with cost 3² = 9

The total cost is 1 + 1 + 4 + 1 + 4 + 4 + 9 = 24.

 分析：

表达式中出现了i的k次方，且n的值十分的大，k很小。

所以尝试用第二类斯特林的公式展开i的k次方。

 

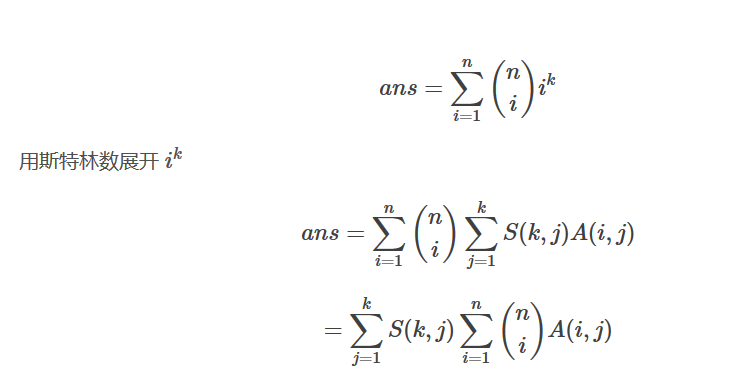
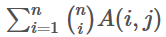是在n里面选i个，再在这i个里面选j个并排序的方案数。

相当于在n个里面取j个，然后考虑剩下的数取或者不取

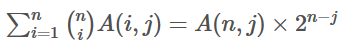
故最终结果为

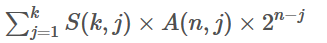
代码如下：

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
typedef long long LL;
const LL MOD=1e9+7;
const int MAXN=5010;
LL stl2[MAXN][MAXN];
LL n,k;
void stl2_init()
{
  for(int i=1;i<=5000;i++)
  stl2[i][i]=1;

  for(int i=1;i<=5000;i++)
   for(int j=1;j<i;j++)
     stl2[i][j]=(stl2[i-1][j-1]+j*stl2[i-1][j]%MOD)%MOD;
}
LL quick_pow(LL a,LL b)
{
    LL ans=1;
    a%=MOD;
    while(b>0)
    {
      if(b&1) ans=(ans*a)%MOD;
      b>>=1;
      a=(a*a)%MOD;
    }
    return ans;
}
LL A(LL n,LL m)
{
    LL ans=1;
  for(int i=n;i>n-m;i--)
   ans=(ans*i)%MOD;
  return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    stl2_init();
    cin>>n>>k;
    LL ans=0;
    for(int j=1;j<=k;j++)
    {
      LL tmp=stl2[k][j]*A(n,j)%MOD*quick_pow(2,n-j)%MOD;
      ans+=tmp;
      ans%=MOD;
    }
    cout<<ans<<endl;
    return 0;
}

 

 

ans=∑i=1n(ni)

ans=∑i=1n(ni)ik