Codeforces Round #409 (rated, Div. 2, based on VK Cup 2017 Round 2) C. Voltage Keepsake

C. Voltage Keepsake

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You have n devices that you want to use simultaneously.

The i-th device uses a_i units of power per second. This usage is continuous. That is, in λ seconds, the device will use λ·a_i units of power. The i-th device currently has b_i units of power stored. All devices can store an arbitrary amount of power.

You have a single charger that can plug to any single device. The charger will add p units of power per second to a device. This charging is continuous. That is, if you plug in a device for λ seconds, it will gain λ·p units of power. You can switch which device is charging at any arbitrary unit of time (including real numbers), and the time it takes to switch is negligible.

You are wondering, what is the maximum amount of time you can use the devices until one of them hits 0 units of power.

If you can use the devices indefinitely, print -1. Otherwise, print the maximum amount of time before any one device hits 0 power.

Input

The first line contains two integers, n and p (1 ≤ n ≤ 100 000, 1 ≤ p ≤ 10⁹) — the number of devices and the power of the charger.

This is followed by n lines which contain two integers each. Line i contains the integers a_i and b_i (1 ≤ a_i, b_i ≤ 100 000) — the power of the device and the amount of power stored in the device in the beginning.

Output

If you can use the devices indefinitely, print -1. Otherwise, print the maximum amount of time before any one device hits 0 power.

Your answer will be considered correct if its absolute or relative error does not exceed 10^- 4.

Namely, let's assume that your answer is a and the answer of the jury is b. The checker program will consider your answer correct if .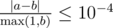

Examples

Input

2 1
2 2
2 1000

Output

2.0000000000

Input

1 100
1 1

Output

-1

Input

3 5
4 3
5 2
6 1

Output

0.5000000000

Note

In sample test 1, you can charge the first device for the entire time until it hits zero power. The second device has enough power to last this time without being charged.

In sample test 2, you can use the device indefinitely.

In sample test 3, we can charge the third device for 2 / 5 of a second, then switch to charge the second device for a 1 / 10 of a second.

 

分析：       首先判断 每秒的供给量与每秒的总消耗量的大小关于 如果大于等于 那么就代表 永远不会消耗完

       否则 二分 完全消耗的的时间，如果能达到就加长时间，不能就缩短时间。

     需要注意的是上界和下界：

     下界可以看作0

    上界详细计算的话是1e10(在n=100000,p==99999,所有的a=1 b=100000下达到）

 自己的问题：

一看题总感觉要么卡时间要么卡精度- -（自己对时间复杂度和double的理解太差了吧）

 赛后发现 即使times=1000 也不会超时

即使上界取到 1e20也没有被精度卡住。。。

代码如下：

#include <bits/stdc++.h>
using namespace std;
#define INF 0x7fffffff
typedef long long ll;
double a[100010];
double b[100010];
int main()
{
   int n,times;    
   double p,mid,l,r;
   while(scanf("%d%lf",&n,&p)!=EOF)
   {
        times=100;
   double    maxt=1e10,mint=0,sum;
   sum=0;
        for(int i=0;i<n;i++)
        {
            scanf("%lf%lf",&a[i],&b[i]);
            sum+=a[i];
        }
        mint=0;   
        if(p>=sum)
        {
        cout<<"-1"<<endl;
        continue;
         }
        l=mint;
        r=maxt;
         // cout<<l<<" "<<r<<endl;
        while(times--)
        {
            mid=(l+r)/2;
            sum=p*mid;
            for(int i=0;i<n;i++)
             {
                 if(mid*a[i]>b[i])
                 sum=sum-(mid*a[i]-b[i]);
             }
             if(sum>0)
             l=mid;
             else
             r=mid;
        }
        printf("%.9f\n",mid);
   }
    return 0;
}