博客作业03--栈和队列
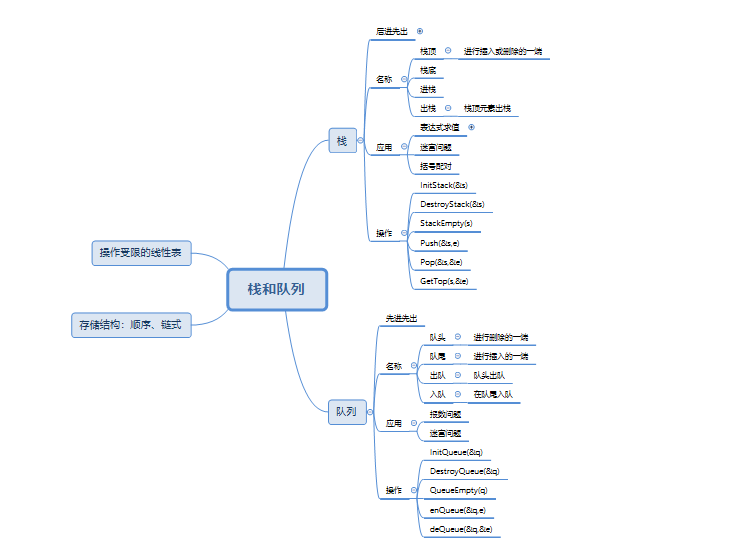
1.学习总结
2.PTA实验作业
2.1 题目1:
7-1 jmu-字符串是否对称
2.2 设计思路
定义ElemType变量e,定义一个栈s,定义整型变量i,flag
为栈创建空间
for i=0 to str[i]不等于'\0'
将字符数组里的字符一一存放入栈
end for
for i=0 to str[i]不等于'\0'
将栈顶元素出栈,赋值给e
如果 str[i]跟e不相等
flag=1
end for
如果flag等于0
说明对称,输出yes
否则,输出no
2.3 代码截图

2.4 PTA提交列表说明

编译器忘了改成c++
2.1 题目2:
7-3 表达式转换
2.2 设计思路
定义栈S,定义整型变量i,j,定义字符变量e和字符数组str
读取字符串
创建栈S并申请空间
while str[i]不等于'\0'
如果是小数点,直接输出
如果是数字,直接输出
否则,如果是+
判断如果是代表正号,直接输出
如果是运算符,当栈顶运算符的优先级高于或等于该运算符则将栈顶运算符输出,直到栈顶运算符的优先级小于该运算符
否则压入栈
否则,如果是-
判断如果是代表负号,直接输出
如果是运算符,当栈顶运算符的优先级高于或等于该运算符则将栈顶运算符输出,直到栈顶运算符的优先级小于该运算符
否则压入栈
否则,如果是(
直接压入栈
否则,如果是)
将遇到第一个左括号之前的运算符都输出
否则,如果是*或/
如果栈顶运算符的优先级高于或等于该运算符则将栈顶运算符输出,直到栈顶运算符的优先级小于该运算符
否则压入栈
end while
当栈不为空时,将栈里的元素都输出
2.3 代码截图





2.4 PTA提交列表说明
第一次没有考虑到小数时的情况,修改过后这个测试点就对了。
运算数前有正负号这个测试点改了蛮久的,不知道正号不用输出来,后面百度题目的时候,看到别人列了测试数据出来,就尝试了一下,没想到就这样对了
2.1 题目3:
7-1 jmu-报数游戏
2.2 设计思路
定义整型变量count=0,e,k,i,n,m,定义队列game
输入n、m的值
如果n小于m
输出error!
否则
初始化队列game
for i=1 to i小于等于n
按顺序入队列
end for
while队列不为空
第一个元素出队列并报数count++
如果报的数count为m
将这个元素输出
count重新赋值为0
否则这个元素继续进入队列
end while
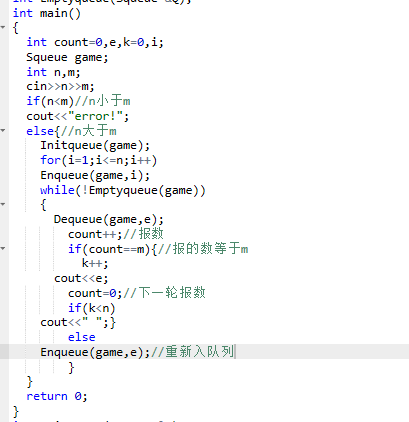
2.3 代码截图
2.4 PTA提交列表说明

第一次做用的是以前的方法,听老师讲了类似的题目后,忽然就懂了怎么用队列做
3.截图本周题目集的PTA最后排名
3.1 栈PTA排名


3.2 队列PTA排名


3.3 我的总分:
209
4. 阅读代码
/*
借助栈 非递归遍历二叉树
2018.4.1
*/
#include<stdio.h>
#include<stdlib.h>
//返回的结果
typedef enum{
ERROR,SUCCESS
}STATUS;
//结点的数据类型
typedef char TREEELEM;
//二叉树结点
typedef struct BinTreeNode{
TREEELEM data;
struct BinTreeNode* lChild,*rChild;
}BinTreeNode,*PtrToBinTree;
typedef PtrToBinTree STACKELEM;
//栈结点
typedef struct StackLinkNode{
STACKELEM data;
struct StackLinkNode * next;
}StackLinkNode,*PtrToLinkStack;
//////////////////////栈//操//作//开//始/////////////////////////////////////
//创建栈
STATUS CreateStackLink(PtrToLinkStack *S){
*S = (PtrToLinkStack)malloc(sizeof(StackLinkNode));
if(*S){
(*S)->next = NULL;
return SUCCESS;
}
return ERROR;
}
//栈判空
bool EmptyStack(PtrToLinkStack S){
if(S->next){
return false;
}
return true;
}
//压栈
STATUS Push(PtrToLinkStack S,STACKELEM e){
PtrToLinkStack temp = (PtrToLinkStack)malloc(sizeof(StackLinkNode));
if(!temp){
return ERROR;
}
temp->data = e;
temp->next = S->next;
S->next = temp;
return SUCCESS;
}
//出栈
STACKELEM Pop(PtrToLinkStack S){
if(EmptyStack(S)){
return NULL;
}
PtrToLinkStack temp = S->next;
S->next = temp->next;
STACKELEM data = temp->data;
free(temp);
return data;
}
//获取栈顶元素
STACKELEM GetTop(PtrToLinkStack S){
return S->next->data;
}
//测试栈操作
//void TestStack(){
// PtrToLinkStack S;
// CreateStackLink(&S);
// int n;
// char c;
// scanf("%d",&n);
// getchar();
// while(n--){
// scanf("%c",&c);
// Push(S,c);
// }
// c = GetTop(S);
// printf("%c\n",c);
// while(!EmptyStack(S)){
// c = Pop(S);
// printf("%c ",c);
// }
// printf("\n");
//}
//////////////////////栈//操//作//结//束/////////////////////////////////////
///////////////////////树//操//作//开//始/////////////////////////////////////
/*
按先序序列输入,如果结点为空请输入“#”
*/
void Create(PtrToBinTree *T){
char c;
scanf("%c",&c);
if(c == '#'){
*T = NULL;
return ;
}
*T = (PtrToBinTree)malloc(sizeof(BinTreeNode));
(*T)->data = c;
Create(&((*T)->lChild));
Create(&((*T)->rChild));
}
/*
访问树结点
*/
void Visit(PtrToBinTree p){
if(p){
printf("%c ",p->data);
}
}
/*
中序遍历非递归算法
*/
void NRInOrd(PtrToBinTree T){
PtrToLinkStack S;
CreateStackLink(&S);
PtrToBinTree p = T;
while(p || !EmptyStack(S)){
if(p){
Push(S,p);
p = p->lChild;
} else {
p = Pop(S);
Visit(p);
p = p->rChild;
}
}
printf("\n");
}
/*
先序遍历非递归算法
*/
void NRPreOrd(PtrToBinTree T){
PtrToLinkStack S;
CreateStackLink(&S);
PtrToBinTree p = T;
while(p || !EmptyStack(S)){
if(p){
Visit(p);
Push(S,p);
p = p->lChild;
} else {
p = Pop(S);
p= p->rChild;
}
}
printf("\n");
}
/*
后序遍历非递归算法
*/
void NRPostOrd(PtrToBinTree T){
PtrToLinkStack S;
CreateStackLink(&S);
PtrToBinTree p,r;
p = T;
r = NULL;
while(p || !EmptyStack(S)){
if(p){
Push(S,p);
p = p->lChild;
} else {
p = GetTop(S);
if(p->rChild && p->rChild!=r){
p = p->rChild;
Push(S,p);
p = p->lChild;
} else{
p = Pop(S);
Visit(p);
r = p;
p = NULL;
}
}
}
printf("\n");
}
int main(){
//TestStack();
PtrToBinTree T;
Create(&T);
//中序非递归遍历
NRInOrd(T);
//先序非递归遍历
NRPreOrd(T);
//后序非递归遍历
NRPostOrd(T);
return 0;
}
代码地址
https://gitee.com/MoZhaMiao/codes/qhol864mxi31dzbegnjr244
该代码用栈的方法实现二叉树的先序、中序、后序遍历,最近正好在学二叉树,学习的时候课本用的是递归的方法。
5. 代码Git提交记录截图





 浙公网安备 33010602011771号
浙公网安备 33010602011771号