双端队列
给出一个长度为n的数列\(\{a_i\}\),从左至右进行操作,假设是对第i个数操作,你有以下选择
- 创建一个新的双端队列,并将\(a_i\)入队
- 入队一个已有的双端队列
最后需要满足所有的双端队列会有一种方案首尾相接形成一个新的数列,这个数列单调递增,\(n\leq 2\times 10^5\)。
解
从答案的角度思考问题,最后的数列是一个单调递增的数列,双端队列类似这个数列中的一个一个区间,于是又像是一道区间划分问题,很快反应出这个问题的一个通用性质,也就是一般可以递推。
先构造数列\(\{b_i\}\),令\(b_i=a_i\),再把\(\{b_i\}\)按从小到大排序,构造一个\(\{c_i\}\),\(c_i\)表示\(b_i\)在\(\{a_i\}\)中出现的位置。
现在我们就只要合法地将\(\{b_i\}\)划分成尽可能少的区间,于是根据\(\{c_i\}\),我们发现把\(i\)作为自变量,\(c_i\)作为因变量,那么此时形成一个有一个最低点,最低点两端的图像都是单调的图像,这一段区间就可以作为一个双端队列中的元素,如图。
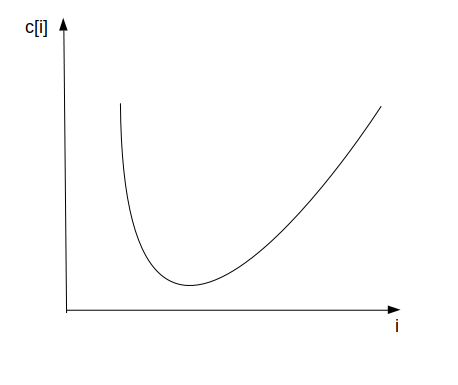
把\(c_i\)看做入队的时间的话,原因在于最低点\(c_i\)表示入队早,而\(b_i\)前的元素都要比\(b_i\)小,而且后入队,因此放在双端队列前面,而\(b_i\)后的元素都要比\(b_i\)大,入队时间靠后,因此后来可以放在双端队列后面,于是\(b_i\)的这样根据\(c_i\)的合法划分,恰恰对应了一个双端队列的操作,再进一步,你会发现实际上我们的考虑角度是针对一个双端队列应该怎么放,而不是一开始传统的思路,一个数字该放在哪个双端队列。
于是问题就变成寻找这样一个图形的最少的个数的问题,而又注意到\(\{b_i\}\)相同的一段元素时,它们的\(\{c_i\}\)中的元素可以自由交换,我们不妨将之看成一个整体,内部按\(\{c_i\}\)排序,也就是刚开始\(\{b_i\}\)排序的时候先按大小为关键字排序,相同时再按位置排序,于是它可以形成一下两幅图的图形,记这段相同的元素的位置为\(i\sim j\),
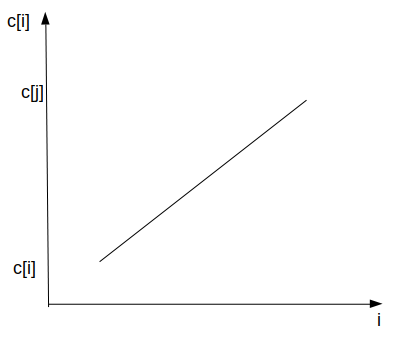
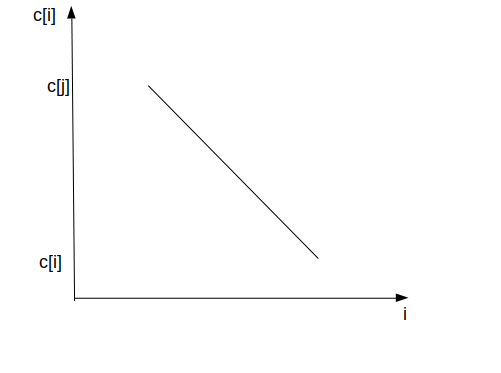
容易知道图形的最大值为\(c_j\),最小值为\(c_i\),设l表示前\(i-1\)个元素的最后一个区间的最后一个元素的所对应的因变量,设j为前i-1个元素最后一个区间所需要表现的状态(0表示接下来这个函数要表现递减,1表示要递增),于是我们可以进行分类讨论,如果
- j=0
\(c[j]<l\),那么此时区间\(i\sim j\)可以接上前面的函数图像保证图像合法,仍然保证函数在递减,对应了这两个区间可以合并成一个区间,对应下图
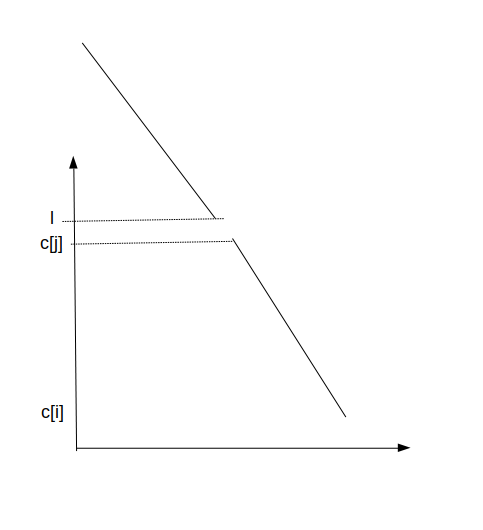
\(c[j]>l\),此时区间\(i\sim j\)可以接上前面的函数,但是不能保证函数一直单调递减,于是后面一截需要单调递增
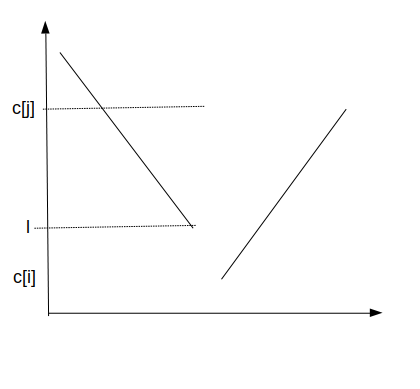
- j=1
\(c[i]>l\),于是后面的函数可以接上前面的函数,仍然保持单调递增。
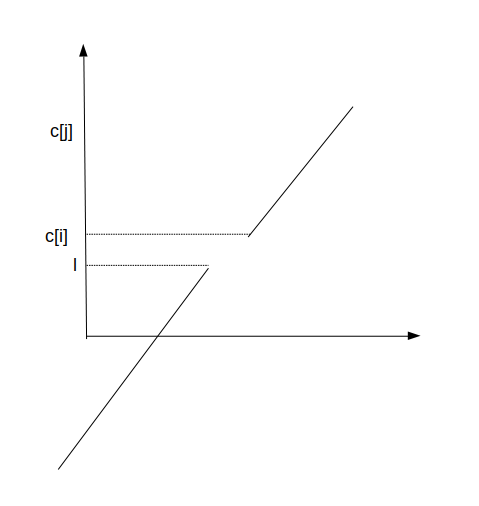
\(c[i]<l\),于是后面的函数无论如何也接不上前面的函数,故需要开一个新的区间。
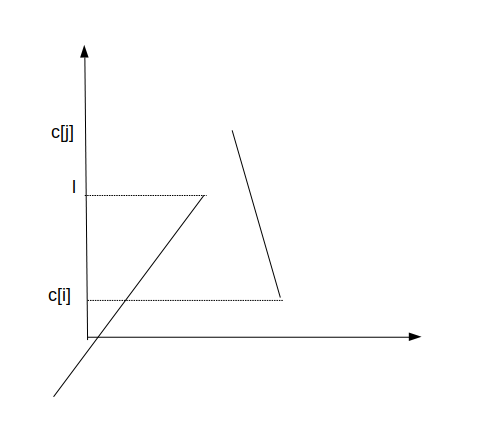
因此,我们就可以在\(O(nlog(n))\)解决这道题目。
最后,注意到这是一个数列的问题,不妨总结一下数列问题的解决办法
从性质上看,一可以根据逆序对个数和奇偶性与问题的关系,二可以把\(a_i\)排序构造一个新的数列\(\{b_i\}\),再构造一个\(\{c_i\}\)记录\(\{b_i\}\)第i个元素在\(\{a_i\}\)中出现的位置,三是构造数列\(\{b_i\}\),令\(b_i=a_i-i\),四是最长上升子序列的长度和个数与原问题的关系。
从角度入手可以考虑第i个位置,前i个位置,相邻位置,常用办法是微扰法,集合问题可以通过排序转成数列问题。
代码很简单,思维很难,多看几遍就可以了,实在看不懂可以问我。
参考代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#define il inline
#define ri register
#define Size 200050
#define intmax 0x7fffffff
using namespace std;
struct D{
int a,b;
il bool operator<(const D&x)const{
return a==x.a?b<x.b:a<x.a;
}
}d[Size];
il void read(int&);
int main(){
int n,ans(0);read(n);
for(int i(1);i<=n;++i)
read(d[i].a),d[i].b=i;
sort(d+1,d+n+1),d[n+1].a=intmax;
for(int i(1),j,k(1),l(intmax);i<=n;i=j+1){
j=i;while(d[j].a==d[j+1].a)++j;
if(k){
if(d[i].b>=l)l=d[j].b;
else ++ans,k^=1,l=d[i].b;
}
else{
if(d[j].b<=l)l=d[i].b;
else k^=1,l=d[j].b;
}
}printf("%d",ans);
return 0;
}
il void read(int &x){
x^=x;ri char c;while(c=getchar(),c==' '||c=='\n'||c=='\r');
ri bool check(false);if(c=='-')check|=true,c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
if(check)x=-x;
}

