Computer
给出一棵有n个节点的无根树，给出\(w[x][y]\)表示x与y的边权，现在询问每个点的到达其他点的最长路径长度（显然不能选它自己）,\(n\leq 10000\)。
解
思维预处理
显然为树形递推题目，又要求多个节点的性质，考虑二次递推+换根法，没有根节点，先钦定1为根节点，设\(A[x]\)为以x为根的子树内x的最大路径长度，显然有
边界：根节点为0
于是来考虑换根
发现问题
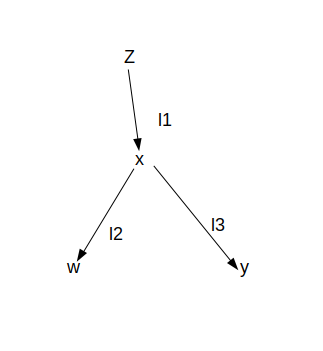
按照老套路，设\(B[x]\)为x的最长路径长度，如图，显然当\(B[x]\)的最优解又y求出，那么求\(B[y]\)时，就不能使用\(\max(B[x],A[x])\)了。
解决问题
理解一：不包括思想（lsy大帝）
既然最优解不能包括y的话，我们设\(b[x][y]\)为求\(B[x]\)的最优解不使用y的值，初始化为求\(A[x]\)时不用y的最优解，如果处理出了这个，那么从x换到y时，\(B[y]=\max(b[x][y]+l3,A[y])\)。
现在考虑如何快速求出\(b[x][y]\)，注意到求A时，我们枚举x的子节点时，如果y成为最优解的决策，那么记录下它，枚举一下它的兄弟，这个因为y只有一个，故为\(O(n)\)，然后就可以暴力求出\(b[x][y]\)，对于w，y的兄弟，它不是最优解，所以显然\(b[x][w]=A[y]+l3\)。
于是对于在换根时的处理，我们就要只要把它和从x上面引入来的z的路径长度取个max即可正确求出\(c[x][y]\)，而这个是很好维护的。
理解二：最优解次优解（czf大神）
既然最优解包括了y，我就想办法用最少的空间不包括y，显然次优解可以解决这个问题，设\(a[x]\)为求\(A[x]\)的次优解，同含义\(b[x]\)，对于\(a[x]\)不难得知求出为\(O(n)\)，用它初始化\(b[x]\),现在考虑维护在从x换到y时的\(b[y]\)，于是发现构成\(b[y]\)的可能性，只有它经过兄弟到y的距离，和从z上面引入的路径，理解1已经告诉我们是\(O(n)\)了，于是可以求出\(b[y]\)。
理解三：暴力维护（一个蠢的要死已经失去所有潜力的菜鸡）
发现事实上这样的这样的难处理点很少，一个节点的儿子中有且仅有一个这样满足条件的点，于是考虑暴力维护它，兄弟照套路维护，在从x换到y的时候，y的最优解的组成只有从经过z从上面来的路径，还有经过它的兄弟到达y的路径，和y以下的路径（\(A[y]\)已经保存了这个），前两者去个max，记做\(czf\),设个数组\(lsy[x]\)表示求\(B[x]\)所用的决策节点，特别地，当\(lsy[x]=0\)，代表接下来的换根操作无需考虑，先用\(A[x]\)的最有决策点初始化它，于是当\(czf>A[y]\)时，令\(B[y]=czf,pre[y]=0\),否则\(B[y]=A[y],pre[y]\)不变。
参考代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#define il inline
#define ri register
#define ll long long
using namespace std;
struct point{
int next,to,w;
}ar[20050];
bool check[10015];
ll dp[10015],db[10015];
int at,head[10015],pre[10015];
void dfs1(int),dfs2(int,ll);
il void link(int,int,int);
int main(){
int n;
while(scanf("%d",&n)!=EOF){
memset(dp,0,sizeof(dp));
at&=0,memset(head,0,sizeof(head));
for(int i(2),u,l;i<=n;++i)
scanf("%d%d",&u,&l),
link(i,u,l),link(u,i,l);
dfs1(1),dfs2(1,0);
for(int i(1);i<=n;++i)
printf("%lld\n",db[i]);
}
return 0;
}
void dfs2(int x,ll lsy){
check[x]&=0;ll czf(0);
for(ri int i(head[x]);i;i=ar[i].next)
if(check[ar[i].to]){
if(pre[x]==i)continue;
if(db[ar[i].to]<db[x]+ar[i].w)
db[ar[i].to]=db[x]+ar[i].w,pre[ar[i].to]=0;
czf=max(czf,dp[ar[i].to]+ar[i].w);
dfs2(ar[i].to,db[x]+ar[i].w);
}
if(pre[x]){
czf=max(lsy+ar[pre[x]].w,czf+ar[pre[x]].w);
if(db[ar[pre[x]].to]<czf)
db[ar[pre[x]].to]=czf,pre[ar[pre[x]].to]=0;
dfs2(ar[pre[x]].to,czf);
}
}
void dfs1(int x){
check[x]|=true;
for(int i(head[x]);i;i=ar[i].next){
if(check[ar[i].to])continue;dfs1(ar[i].to);
if(dp[ar[i].to]+ar[i].w>dp[x])
dp[x]=dp[ar[i].to]+ar[i].w,pre[x]=i;
}db[x]=dp[x];
}
il void link(int u,int v,int w){
ar[++at].to=v,ar[at].w=w;
ar[at].next=head[u],head[u]=at;
}
