[NOI2001]炮兵阵地
有一个\(n\times m\)的网格，第i行第j列有一个字符\(c[i][j]\)=P or H,分别表示此处为平原和山，只有平原才能放炮，炮的攻击范围为向上下左右2格，如图黑色为攻击范围，灰色为放炮的位置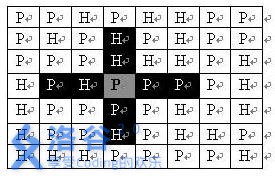
，现在要求求出网格图中最多可以放炮的个数，并保证炮炮之间不能互相攻击，\(n\leq 100,m\leq 10\)。
解
m的范围已经告诉你可以进制压缩，但是状态却有三种，于是延伸两种办法
法一：二进制压缩
二进制当然是最快的，于是可以设\(f[i][j][k]\)表示处理到第i行且第i行的状态为j,第i-1行状态为k的能放的最多的炮的数量，显然设j中有1的位置为有炮的位置，而注意到这样做会超时，非法状态太多，于是可以预处理每一行合法的状态，以此作为转移依据，设\(a[i][j]\)为第i行第j个合法状态的二进制数，自然\(f[i][j][k]\)的j对应的是\(a[i][j]\)，k对应的是\(a[i-1][k]\)，并预处理\(B[i]\)表示i的二进制位下有多少个1,于是我们有
\[f[i][j][k]=\max_{l=0}^{2^m-1}(f[i-1][k][l])+B[a[i][j]](!(a[i][j]\&a[i-1][k])\&\&!(a[i][j]\&a[i-2][l])\&\&!(a[i-1][k]\&a[i-2][l]))
\]
边界：\(f[1][i][0]=bit[a[1][i]],i=1,2,..,|a[1]|\)
答案：\(\max_{i=j=0}^{2^m-1}(f[n][i][j])\)
参考代码：
#include <iostream>
#include <cstdio>
#define il inline
#define ri register
using namespace std;
char M[15];
int a[101][501],at[101],
dp[101][501][501],bit[2048];
il int max(int,int);
int main(){
int n,m,li;
scanf("%d%d",&n,&m),li=(1<<m)-1;
for(int i(0);i<=li;++i)
for(int j(m-1);j>=0;--j)
if(i>>j&1)++bit[i];
for(int i(1);i<=n;++i){
scanf("%s",M);
for(int j(0),k,l;j<=li;++j){
for(l=100,k=m-1;k>=0;--k)
if(j>>k&1){if(M[k]=='H'||l-k<3)break;l=k;}
if(k<0)a[i][++at[i]]=j;
}
}++at[0];
for(int i(1);i<=at[1];++i)dp[1][i][1]=bit[a[1][i]];
for(int i(2);i<=n;++i)
for(int j(1);j<=at[i];++j)
for(int k(1);k<=at[i-1];++k){
if(a[i][j]&a[i-1][k])continue;
for(int l(1);l<=at[i-2];++l){
if(a[i-2][l]&a[i][j]||a[i-2][l]&a[i-1][k])continue;
dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][l]);
}dp[i][j][k]+=bit[a[i][j]];
}
int ans(0);
for(int i(1);i<=at[n];++i)
for(int j(1);j<=at[n-1];++j)
ans=max(ans,dp[n][i][j]);
printf("%d\n",ans);
return 0;
}
il int max(int a,int b){
return a>b?a:b;
}
法二：三进制压缩
因为存在三种状态，所以自然的想法是三进制压缩，2表示有炮，1表示炮的上下左右的一格攻击范围，因为多进制的合法判断的速度远远不如二进制，于是我们需要dfs实现转移，而且要尽可能地多多特判非法状态。
#include <iostream>
#include <cstdio>
#include <cstring>
#define il inline
#define ri register
using namespace std;
char M[11];
int bit[101],dp[101][59050],
b2[59051],y,e,m;
void dfs(int,int,int);
il void read(int&);
int main(){
int n;read(n),read(m),bit[0]=1;
for(int i(1);i<=10;++i)bit[i]=bit[i-1]*3;
for(int i(0),j;i<bit[m];++i)
for(j=0;j<m;++j)
if(i/bit[j]%3==2)++b2[i];
memset(dp,-127,sizeof(dp)),dp[0][0]=0;
for(y=0;y<n;++y){
scanf("%s",M);
for(e=0;e<bit[m];++e){
if(dp[y][e]<0)continue;
dp[y][e]+=b2[e],dfs(0,0,-100);
}
}int ans(0);
for(int i(0);i<bit[m];++i)
if((dp[n][i]+=b2[i])>ans)ans=dp[n][i];
printf("%d",ans);
return 0;
}
void dfs(int x,int f,int l){
if(x==m)
return (void)(dp[y+1][f]=max(dp[y][e],dp[y+1][f]));
if(e/bit[x]%3==2)dfs(x+1,f+bit[x],l);
else{
dfs(x+1,f,l);
if(!(e/bit[x]%3)&&M[x]=='P')
if(x-l>2)dfs(x+1,f+bit[x]*2,x);
}
}
il void read(int &x){
x&=0;ri char c;while(c=getchar(),c<'0'||c>'9');
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
}
