[AHOI2012]树屋阶梯

[AHOI2012]树屋阶梯

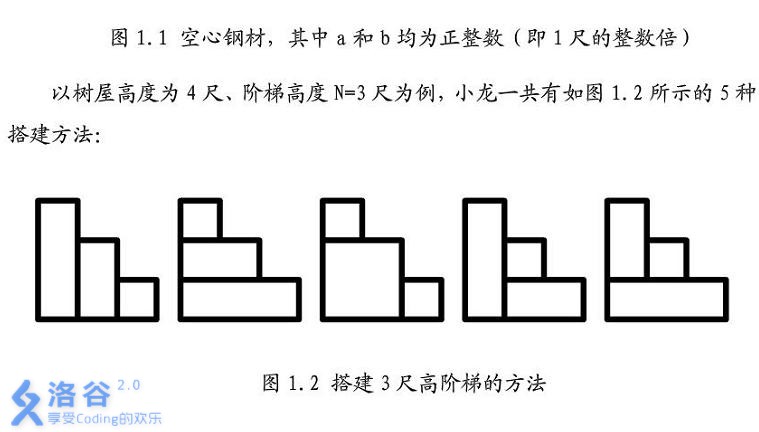
要构成一个\(n\times n\)的阶梯形图形，如图，但你只能用n个长方形构成这个图形，询问其方案数，\(1<=N<=500\)。

解

其实注意到题目很简单，而且还是很奇怪的组合计数，在加上样例\(1,2,5,14\),你就能猜到这是一个catalan数列。

但还是按照正规的思路来，组合计数问题，显然无法推出通项公式，于是考虑递推方程，设\(f[n]\)表示长度为n的阶梯形图形划分方案数，问题在于接下无法根据策略转移，考虑划分，尝试把它划分成两个完整的阶梯，于是我们完全可以利用一个端点在最左下角的，一个端点在阶梯上的点的正方形划分问题，于是有

\(f[n]=f[1]f[n-1]+f[2]f[n-2]+...f[n-1][1]\)

边界:\(f[1]=1\)

于是很快反应过来，这就是catalan数的递推公式，于是不用递推方程，它只是负责证明，接下来套用其公式，利用高精阶乘分解质因数的方法即可。

参考代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#define il inline
#define ri register
using namespace std;
struct lll{
    short num[5000];
    il lll(){num[0]=1;}
    il void clear(){
        memset(num,0,sizeof(num)),num[0]=1;
    }
    il void read(){
        string s;cin>>s,num[0]=s.size();
        for(ri int i(1);i<=num[0];++i)
            num[i]=s[num[0]-i]-48;
    }
    il void print(){
        for(ri int i(num[0]);i;--i)
            putchar(num[i]+48);
    }
    il void operator=(int x){
        num[0]&=0;
        while(x)num[++num[0]]=x%10,x/=10;
    }
    il lll operator*(lll x){
        lll y;y.clear();
        for(ri int i(1),j,k;i<=num[0];++i){
            k&=0;
            for(j=1;j<=x.num[0];++j)
                y.num[i+j-1]+=num[i]*x.num[j]+k,
                    k=y.num[i+j-1]/10,y.num[i+j-1]%=10;
            y.num[i+x.num[0]]+=k;
        }y.num[0]=num[0]+x.num[0];
        while(!y.num[y.num[0]]&&y.num[0]>1)--y.num[0];
        return y;
    }template<class free>
    il lll operator^(free y){
        lll x(*this),ans;ans=1;
        while(y){
            if(y&1)ans=ans*x;
            x=x*x,y>>=1;
        }return ans;
    }
}xdk[201];
bool check[1001];
int prime[201],pt;
il void cat(int),sieve(int);
int main(){
    int n;scanf("%d",&n);
    sieve(n<<1),cat(n);
    return 0;
}
il void sieve(int n){
    check[1]|=true;
    for(ri int i(2),j;i<=n;++i){
        if(!check[i])prime[++pt]=i,xdk[pt]=i;
        for(j=1;j<=pt&&i*prime[j]<=n;++j){
            check[i*prime[j]]|=true;
            if(!(i%prime[j]))break;
        }
    }
}
il void cat(int n){
    lll ans;ans=1;
    int n2(n<<1),i,j,wch(n+1),tr;
    for(i=1;i<=pt;++i){
        tr&=0;
        for(j=n2;j;j/=prime[i])tr+=j/prime[i];
        for(j=n;j;j/=prime[i])tr-=j/prime[i]<<1;
        while(!(wch%prime[i]))wch/=prime[i],--tr;
        ans=ans*(xdk[i]^tr);
    }ans.print();
}