诸侯放置

诸侯放置

给你一个长n网格图，还给你k个棋子，放入格子中，询问保证任意一行一列不存在2个及以上的棋子的方案数\(mod\ 504\)，如图所示为一长3的网格图和2个棋子的方案，n≤l00，k≤2n2-2n+1。

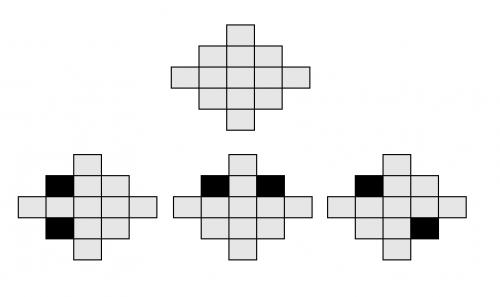
解

显然是错排问题，关键在于构造出高度递增，而根据错排自由定理，错拍问题中，行列交换互不影响，于是可以构造成高度递增，接下来直接套错排问题经典递推方程(f[i][j]表示填到i列，已经填了j颗棋子的方案数，h[i]表示第i列的高度)即可。

\[f[i][j]=f[i-1][j]+f[i-1][j-1]\times(h[i]-j+1) \]

边界:\(f[0][0]=1\)

答案:\(f[2n-1][k]\)

参考代码：

#include <iostream>
#include <cstdio>
#define il inline
#define ri register
#define yyb 504
using namespace std;
int dp[205][205],h[205];
int main(){
    int n,k,i,j,ans(0),li;
    scanf("%d%d",&n,&k),li=(n<<1)-1;
    if(k>li)return puts("0"),0;
    for(i=1;i<li;i+=2)h[i]=i,h[i+1]=i;h[li]=i;
    for(i=-1;i<=li;++i,dp[i][0]=1)
        for(j=1;j<=i&&j<=k;++j)
            dp[i][j]=(dp[i-1][j]+dp[i-1][j-1]*(h[i]-j+1)%yyb)%yyb;
    printf("%d",dp[li][k]);
    return 0;
}