车的放置

车的放置

有如下网格，a，b，c，d代表网格数

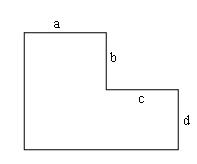
现在有k辆车放入这个棋盘，要求每一行每一列不超过一辆车，询问其方案数mod 100003,a，b，c，d，k≤1000。

解

法一：通项公式

注意到从左边开始划分问题，会存在分类讨论的麻烦，于是考虑从右边开始分类讨论，显然我们需要枚举有多少辆车方法右半部分，设其为i，然后它的方案数为\(C_c^iP_d^i\),接着剩下的车放入左半部分必然会受到右半部分的影响，所以只能有\(C_a^{k-i}P_{b+d-i}^{k-i}\),总上有

\[ans=\sum_{i=0}^{k}C_c^iP_{d}^{i}C_{a}^{k-i}P_{b+d-i}^{k-i} \]

预处理出阶乘以及逆元，套公式枚举即可，时间复杂度\(O(k)\)。

参考代码：

#include <iostream>
#include <cstdio>
#define il inline
#define ri register
#define ll long long
#define gzy 2000
#define yyb 100003
using namespace std;
int jc[2001],jv[2001];
il void prepare();
il int pow(int,int),C(int,int),P(int,int);
int main(){
    int a,b,c,d,k,ans(0),i;
    scanf("%d%d%d%d%d",&a,&b,&c,&d,&k),prepare();
    for(i=0;i<=k;++i)
        (ans+=(ll)C(c,i)*P(d,i)*C(a,k-i)%yyb*P(d+b-i,k-i)%yyb)%=yyb;printf("%d",ans);
    return 0;
}
il int P(int n,int r){
    if(n<r)return 0;
    return (ll)jc[n]*jv[n-r]%yyb;
}
il int C(int n,int r){
    if(n<r)return 0;
    return (ll)jc[n]*jv[r]*jv[n-r]%yyb;
}
il void prepare(){
    int i;
    for(i=jc[0]=1;i<=gzy;++i)jc[i]=(ll)jc[i-1]*i%yyb;
    jv[gzy]=pow(jc[gzy],yyb-2);
    for(i=gzy,jv[0]=1;i>1;--i)jv[i-1]=(ll)jv[i]*i%yyb;
}
il int pow(int x,int y){
    int ans(1);while(y){
        if(y&1)ans=(ll)ans*x%yyb;
        x=(ll)x*x%yyb,y>>=1;
    }return ans;
}

法二：递推方程

显然要表现出车的个数，还要表现出填到第几列，在进行排列，于是设
\(f[i][j]\)表示后i列，填了j辆车的方案数，因为左边必然受到右边影响，而影响因素存在高度，还设\(h(i)\)表示第i列高度，于是我们有

\[f[i][j]=f[i+1][j-1]\times (h(i)-j+1)+f[i+1][j] \]

边界：\(f[a+c+1][0]=1\)

答案：\(f[1][k]\)

参考代码：

#include <iostream>
#include <cstdio>
#define il inline
#define ri register
#define ll long long
#define yyb 100003
using namespace std;
int v[2001],dp[2001][2001];
int main(){
    int a,b,c,d,k,i,j;
    scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
    for(i=1;i<=c;++i)v[i]=d;
    for(i=c+1;i<=a+c;++i)v[i]=b+d;
    for(j=-1;j<=a+c;++j,dp[j][0]=1)
        for(i=1;i<=k&&i<=j;++i)
            (dp[j][i]=dp[j-1][i]+(ll)dp[j-1][i-1]*(v[j]-i+1)%yyb)%=yyb;
    printf("%d",dp[a+c][k]);
    return 0;
}