决策树

认识决策树

决策树思想的来源非常朴素，程序设计中的条件分支结构就是if-then结构，最早的决策树就是利用这类结构分割数据的一种分类学习方法

怎么理解这句话？通过一个对话例子

 

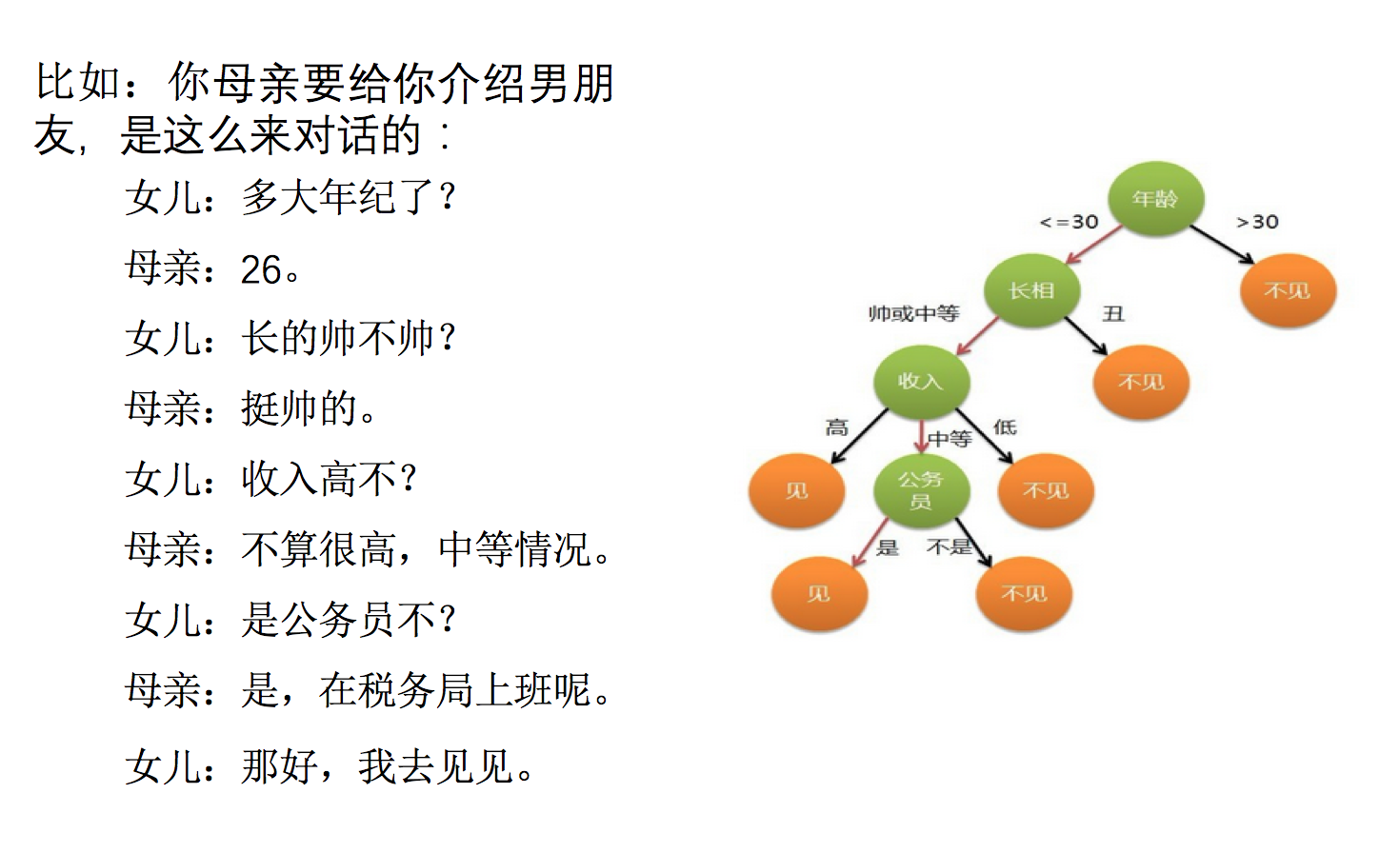
 想一想这个女生为什么把年龄放在最上面判断！！！！！！！！！

决策树分类原理详解

为了更好理解决策树具体怎么分类的，我们通过一个问题例子？

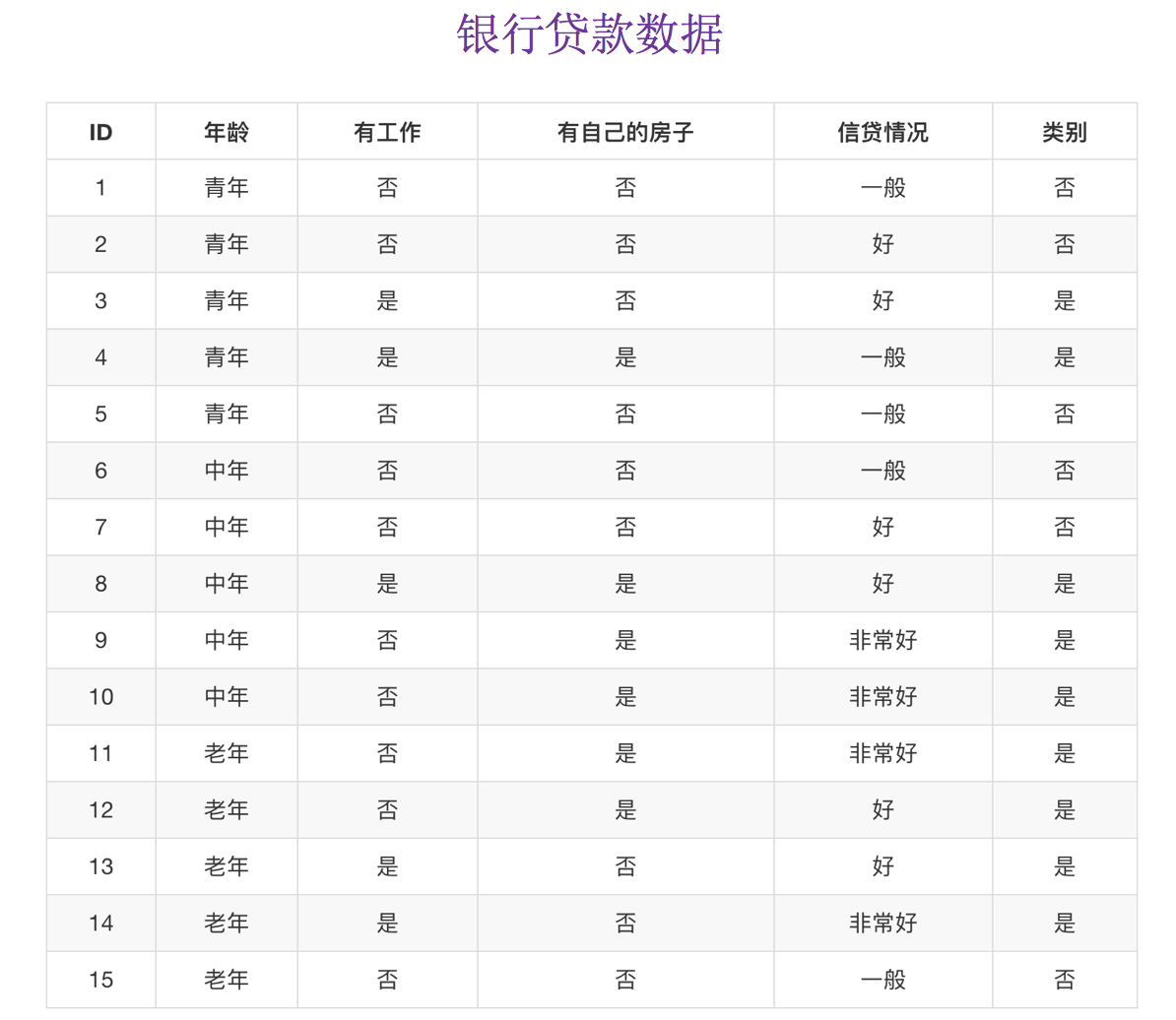
如何对这些客户进行分类预测？你是如何去划分？

有可能你的划分是这样的

 

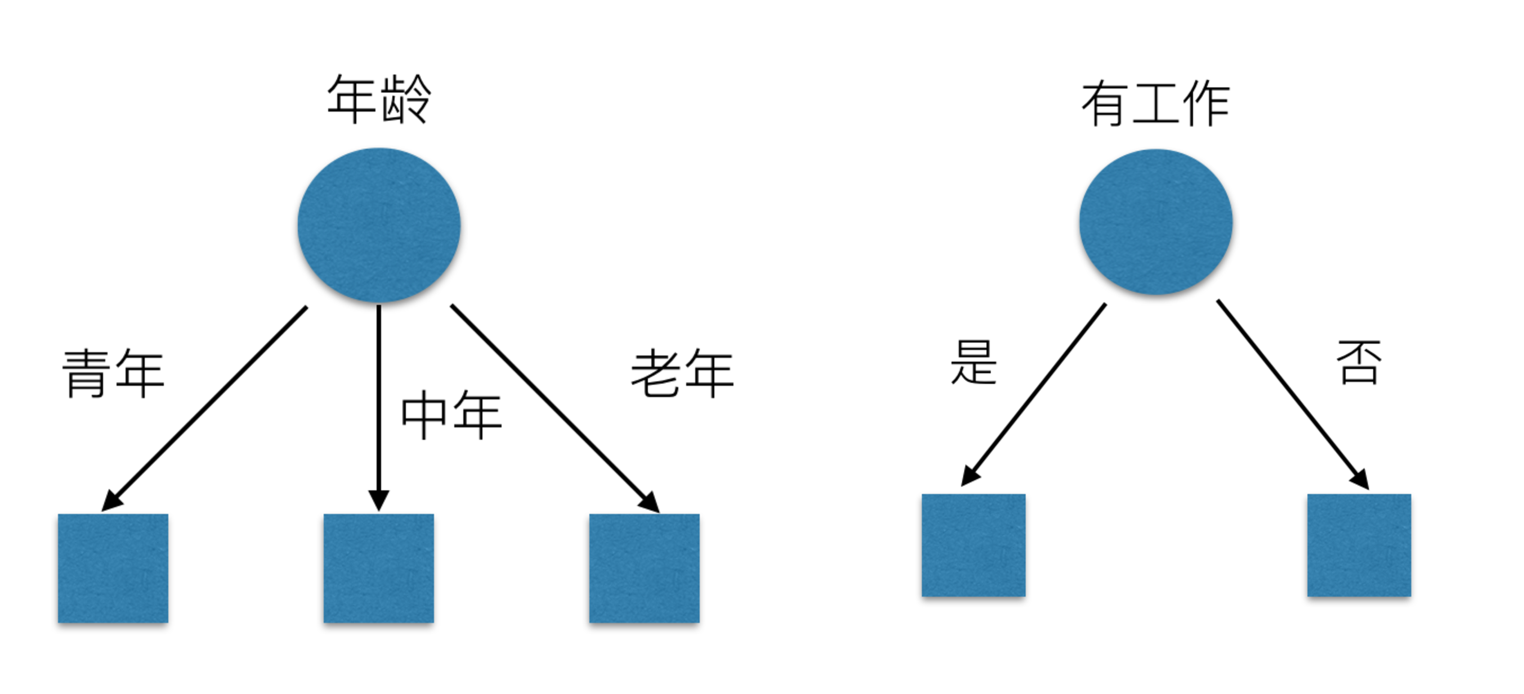
 那么我们怎么知道这些特征哪个更好放在最上面，那么决策树的真是划分是这样的

 

 

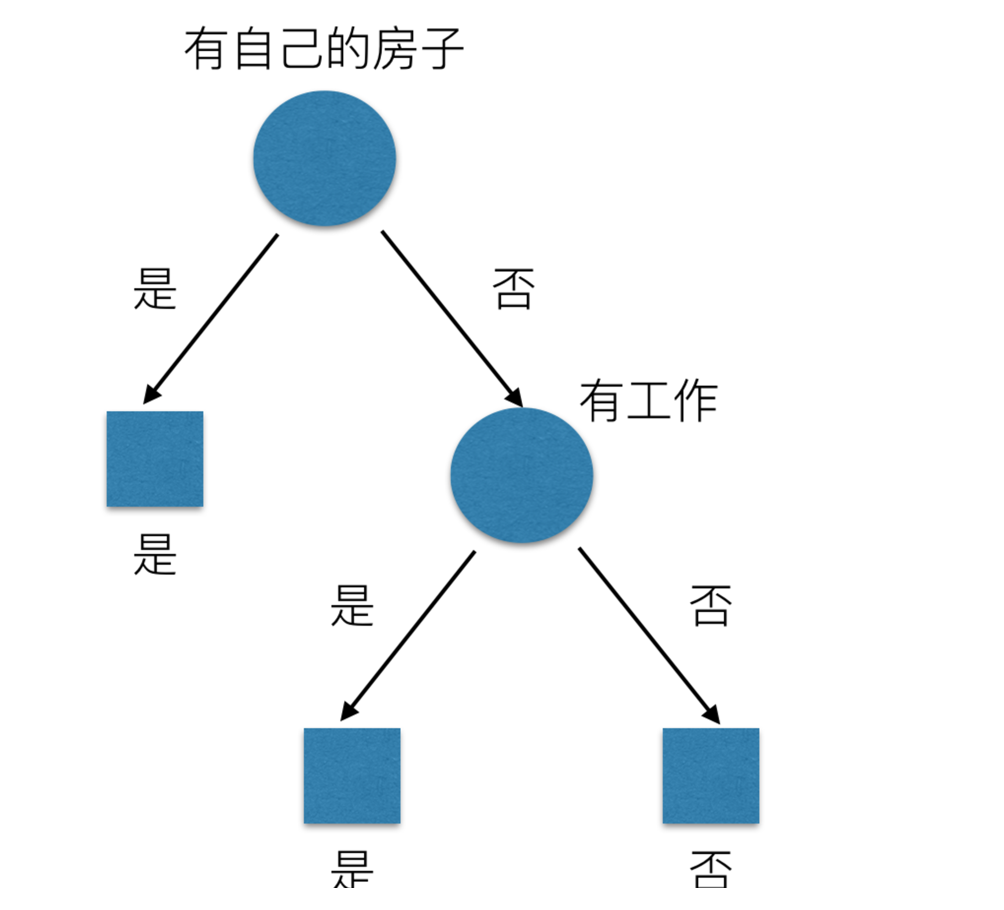
原理

• 信息熵、信息增益等

信息熵

H的专业术语称之为信息熵，单位为比特

总结（重要）

• 信息和消除不确定性是相联系的

当我们得到的额外信息（球队历史比赛情况等等）越多的话，那么我们猜测的代价越小（猜测的不确定性减小）

问题： 回到我们前面的贷款案例，怎么去划分？可以利用当得知某个特征（比如是否有房子）之后，我们能够减少的不确定性大小。越大我们可以认为这个特征很重要。那怎么去衡量减少的不确定性大小呢？

决策树的划分依据之一------信息增益

定义与公式

特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差，即公式为：

 

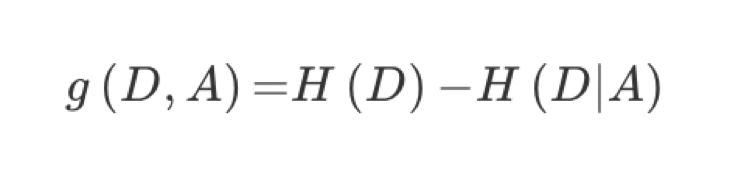
 公式的详细解释：

 

 注：信息增益表示得知特征X的信息而息的不确定性减少的程度使得类Y的信息熵减少的程度

贷款特征重要计算

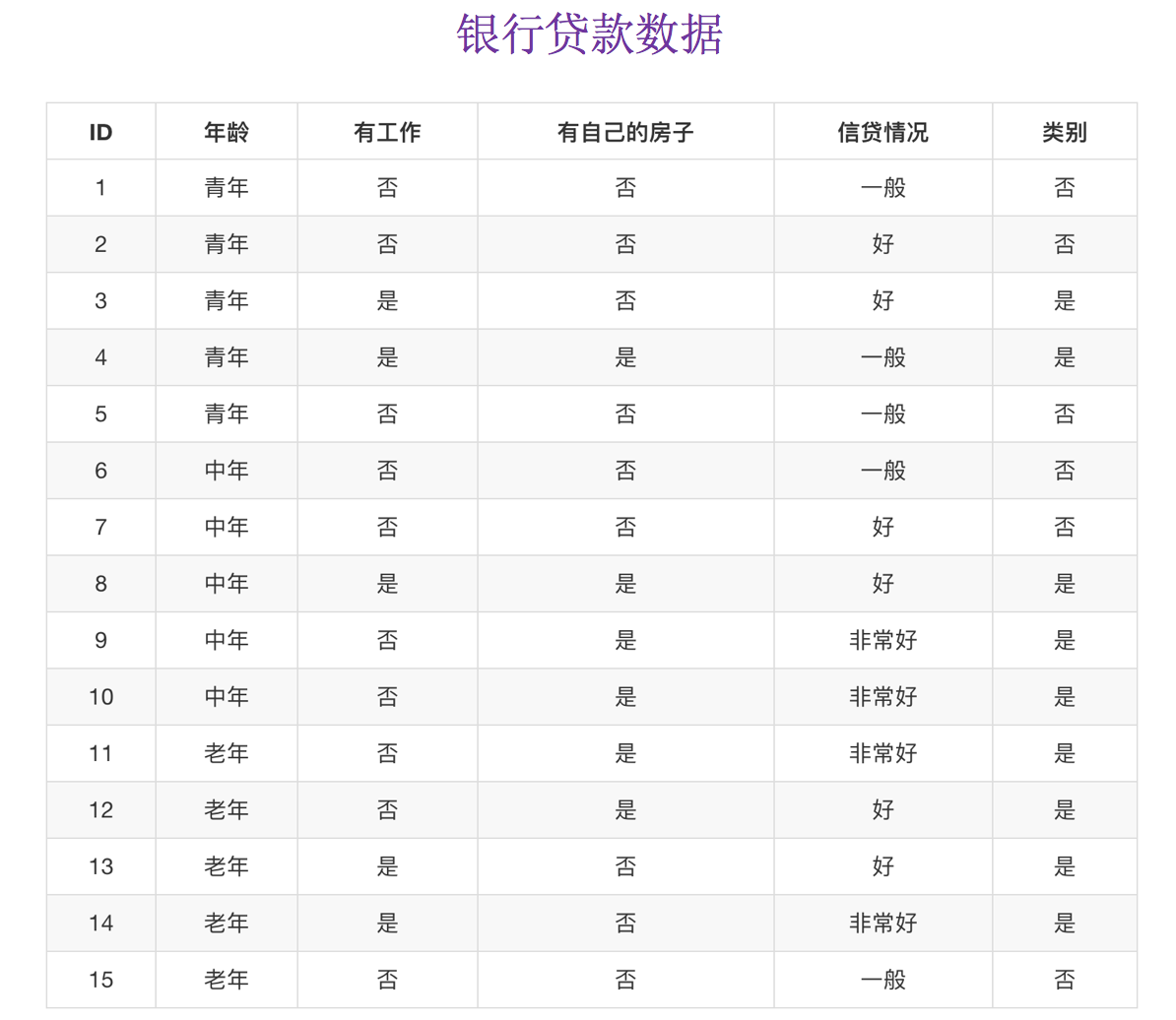
• 我们以年龄特征来计算：

1、g(D, 年龄) = H(D) -H(D|年龄) = 0.971-[5/15H(青年)+5/15H(中年)+5/15H(老年]

2、H(D) = -(6/15log(6/15)+9/15log(9/15))=0.971

3、H(青年) = -(3/5log(3/5) +2/5log(2/5))
H(中年)=-(3/5log(3/5) +2/5log(2/5))
H(老年)=-(4/5og(4/5)+1/5log(1/5))

我们以A1、A2、A3、A4代表年龄、有工作、有自己的房子和贷款情况。最终计算的结果g(D, A1) = 0.313, g(D, A2) = 0.324, g(D, A3) = 0.420,g(D, A4) = 0.363。所以我们选择A3 作为划分的第一个特征。这样我们就可以一棵树慢慢建立

决策树的三种算法实现

当然决策树的原理不止信息增益这一种，还有其他方法。但是原理都类似，我们就不去举例计算。

• ID3
  • 信息增益 最大的准则
• C4.5
  • 信息增益比 最大的准则
• CART
  • 分类树: 基尼系数 最小的准则 在sklearn中可以选择划分的默认原则
  • 优势：划分更加细致（从后面例子的树显示来理解）

决策树API

class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)

• 决策树分类器
• criterion:默认是’gini’系数，也可以选择信息增益的熵’entropy’
• max_depth:树的深度大小
• random_state:随机数种子

其中会有些超参数：max_depth:树的深度大小

• 其它超参数我们会结合随机森林讲解

案例：

鸢尾花种类预测

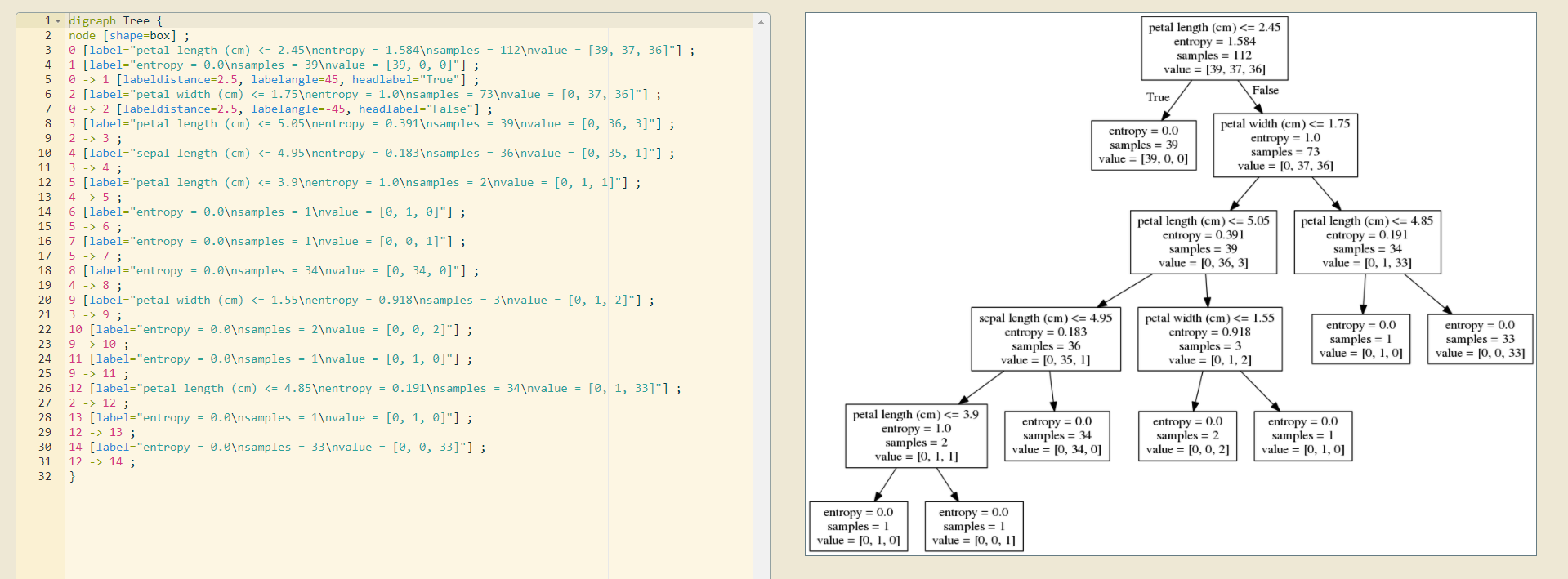
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz
def decision_iris():
    """
    用决策树对鸢尾花进行分类
    :return:
    """
    # 1）获取数据集
    iris = load_iris()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

    # 3）决策树预估器
    estimator = DecisionTreeClassifier(criterion="entropy")
    estimator.fit(x_train, y_train)

    # 4）模型评估
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    # 可视化决策树
    export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)

    return None

if __name__ == "__main__":
    # 代码4：用决策树对鸢尾花进行分类
    decision_iris()

 

 

 

 

 

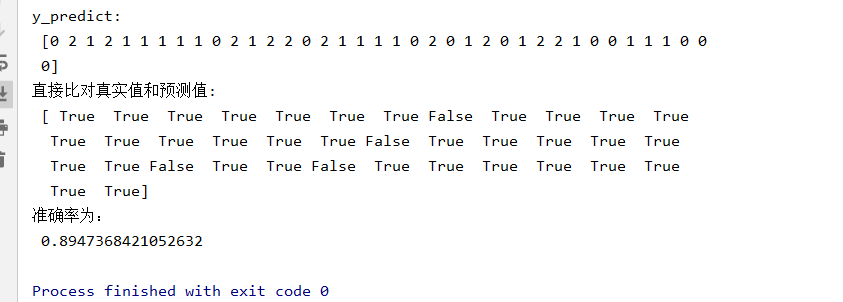
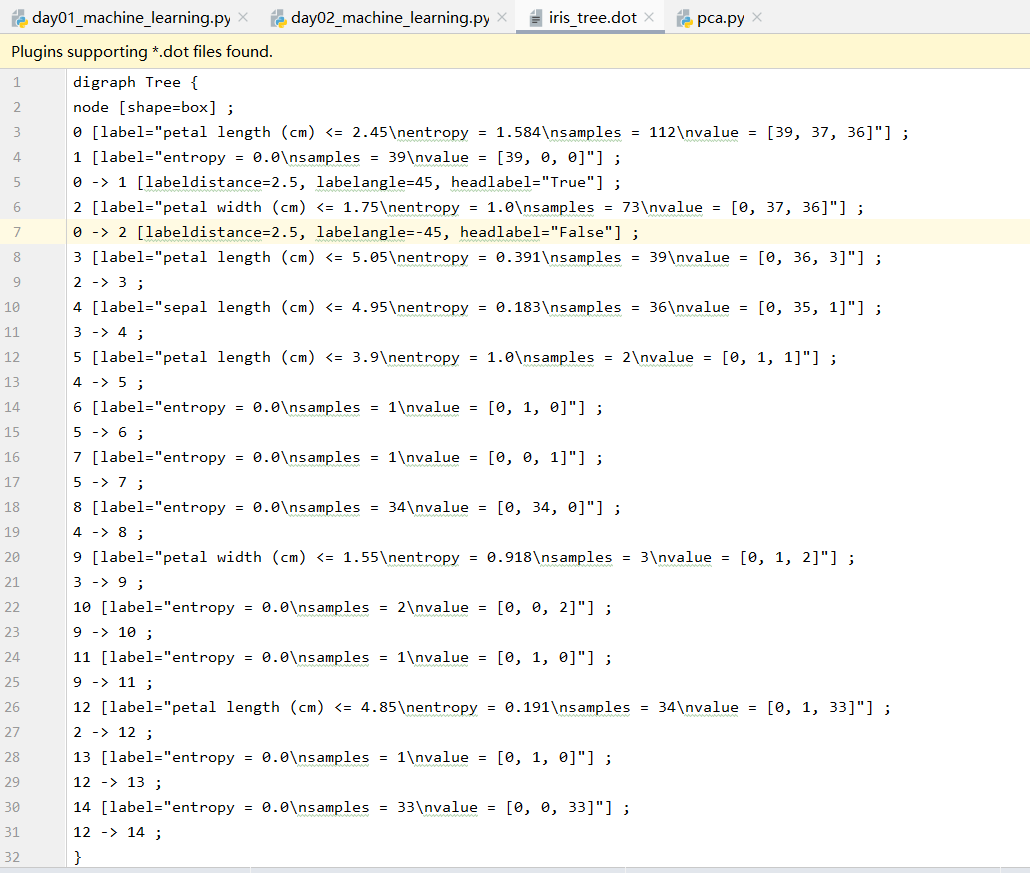
 决策树可视化：

网址：

http://graphviz.herokuapp.com/

 

案例：泰坦尼克号乘客生存预测

泰坦尼克号数据

在泰坦尼克号和titanic2数据帧描述泰坦尼克号上的个别乘客的生存状态。这里使用的数据集是由各种研究人员开始的。其中包括许多研究人员创建的旅客名单，由Michael A. Findlay编辑。我们提取的数据集中的特征是票的类别，存活，乘坐班，年龄，登陆，home.dest，房间，票，船和性别。

乘坐班是指乘客班（1，2，3），是社会经济阶层的代表。

其中age数据存在缺失

 

 

分析

• 选择我们认为重要的几个特征 ['pclass', 'age', 'sex']
• 填充缺失值
• 特征中出现类别符号，需要进行one-hot编码处理(DictVectorizer)
  • x.to_dict(orient="records") 需要将数组特征转换成字典数据
• 数据集划分
• 决策树分类预测

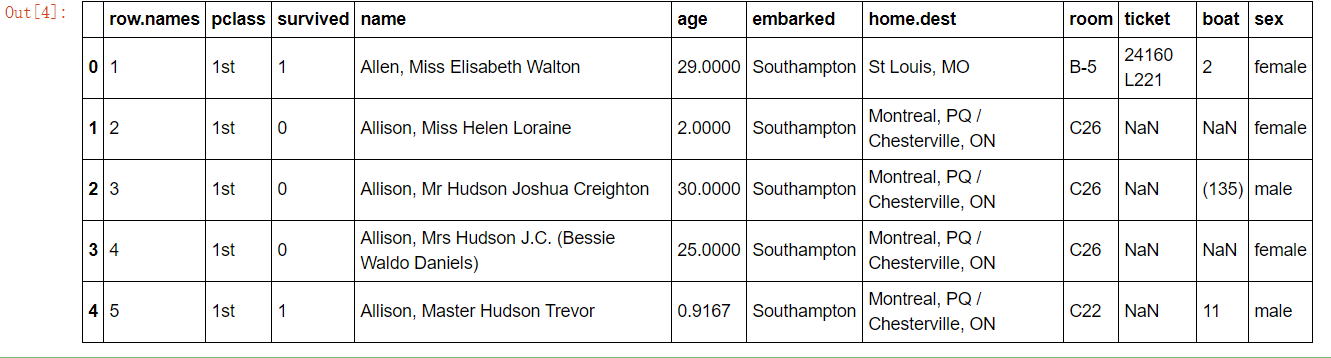
import pandas as pd
# 1、获取数据
path = "http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt"
titanic = pd.read_csv(path)
titanic.head()

 

 

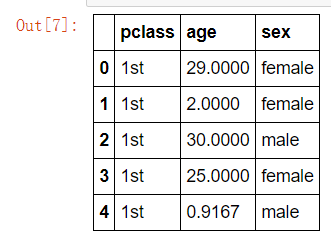
# 筛选特征值和目标值
x = titanic[["pclass", "age", "sex"]]
y = titanic["survived"]
x.head()
y.head()

 

 

 

 

# 2、数据处理
# 1）缺失值处理
x["age"].fillna(x["age"].mean(), inplace=True)
# 2) 转换成字典
x = x.to_dict(orient="records")
from sklearn.model_selection import train_test_split
# 3、数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
# 4、字典特征抽取
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier, export_graphviz
transfer = DictVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 3）决策树预估器
estimator = DecisionTreeClassifier(criterion="entropy", max_depth=8)
estimator.fit(x_train, y_train)

# 4）模型评估
# 方法1：直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)

# 方法2：计算准确率
score = estimator.score(x_test, y_test)
print("准确率为：\n", score)

# 可视化决策树
export_graphviz(estimator, out_file="titanic_tree.dot", feature_names=transfer.get_feature_names())

结果：

y_predict:
 [0 0 0 0 1 1 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0
 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0
 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1
 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1
 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 1 0 0 0 0 0 1 1 1 1 0 0 0 0 0
 0 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 0
 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
 0 1 1 1 0 0 1 1 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1
 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1]
直接比对真实值和预测值:
 831      True
261      True
1210     True
1155     True
255      True
762      True
615      True
507      True
1175     True
301      True
1134     True
177     False
183     False
125     False
1093     True
1304    False
1124     True
798     False
1101     True
1239    False
1153     True
1068    False
846      True
148      True
478      True
642      True
1298     True
540      True
28       True
130      True
        ...  
194      True
663      True
1209     True
117     False
595     False
1151    False
1143     True
1216     True
874      True
246      True
160      True
1208     True
682      True
307      True
67       True
961      True
400      True
923     False
866      True
134      True
613      True
242      True
320     False
829      True
94       True
1146     True
1125    False
386      True
1025    False
337      True
Name: survived, Length: 329, dtype: bool
准确率为：
 0.7811550151975684