Java实现 LeetCode第198场周赛 （题号5464，5465，5466，5467）
这次的题感觉比往常难度大多了
小区便利店正在促销，用 numExchange 个空酒瓶可以兑换一瓶新酒。你购入了 numBottles 瓶酒。
如果喝掉了酒瓶中的酒，那么酒瓶就会变成空的。
请你计算 最多 能喝到多少瓶酒。
示例 1：
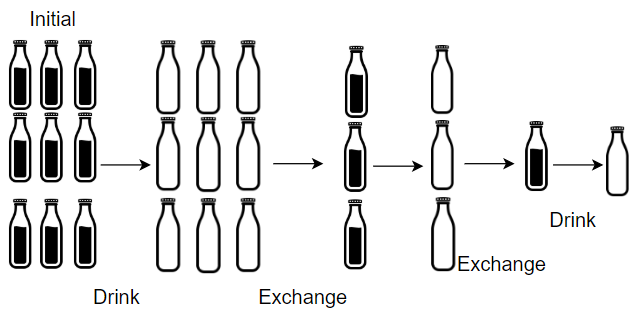
输入：numBottles = 9, numExchange = 3
输出：13
解释：你可以用 3 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 9 + 3 + 1 = 13 瓶酒。
示例 2：
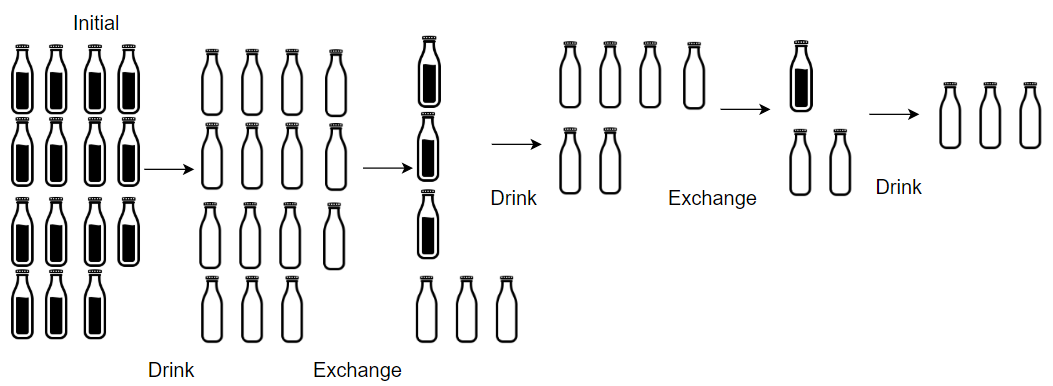
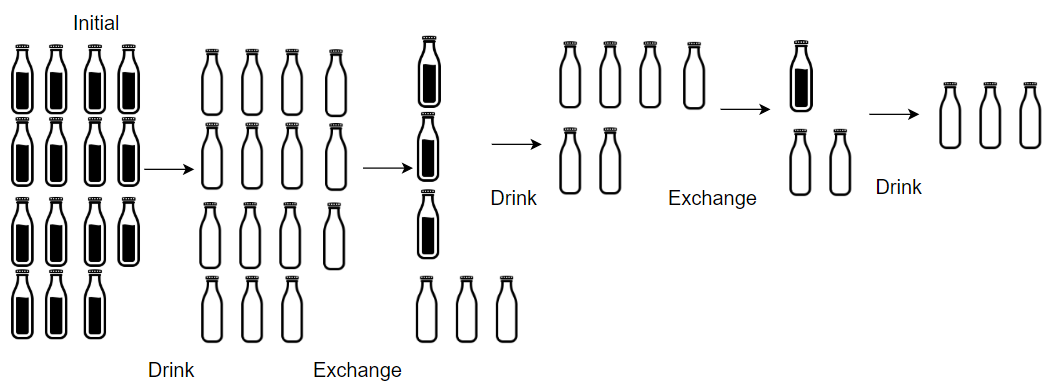
输入：numBottles = 15, numExchange = 4
输出：19
解释：你可以用 4 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 15 + 3 + 1 = 19 瓶酒。
示例 3：
输入：numBottles = 5, numExchange = 5 输出：6
示例 4：
输入：numBottles = 2, numExchange = 3 输出：2
提示：
1 <= numBottles <= 1002 <= numExchange <= 100
这个代码注释比较好，我的那个没写注释，但又懒得加了，该说不说，这个题我小学见过，哈哈😄
class Solution { public int numWaterBottles(int numBottles, int numExchange) { int sum = 0; //空瓶数 int cin = 0; //可喝的酒不为 0 while(numBottles != 0){ sum += numBottles; //空瓶子数 int temp = numBottles + cin; //可换酒 的个数 numBottles = temp / numExchange; //剩余空瓶数 cin = temp % numExchange; } return sum; } }
给你一棵树（即，一个连通的无环无向图），这棵树由编号从 0 到 n - 1 的 n 个节点组成，且恰好有 n - 1 条 edges 。树的根节点为节点 0 ，树上的每一个节点都有一个标签，也就是字符串 labels 中的一个小写字符（编号为 i 的 节点的标签就是 labels[i] ）
边数组 edges 以 edges[i] = [ai, bi] 的形式给出，该格式表示节点 ai 和 bi 之间存在一条边。
返回一个大小为 n 的数组，其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。
树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。
示例 1：
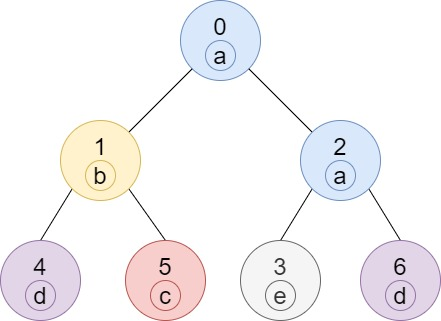
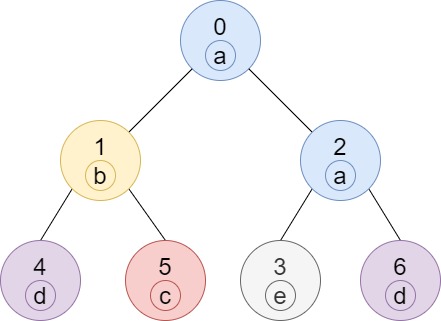
输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd" 输出：[2,1,1,1,1,1,1] 解释：节点 0 的标签为 'a' ，以 'a' 为根节点的子树中，节点 2 的标签也是 'a' ，因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。 节点 1 的标签为 'b' ，节点 1 的子树包含节点 1、4 和 5，但是节点 4、5 的标签与节点 1 不同，故而答案为 1（即，该节点本身）。
示例 2：
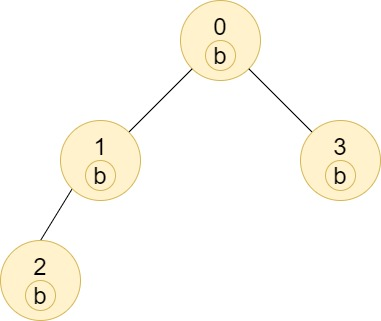
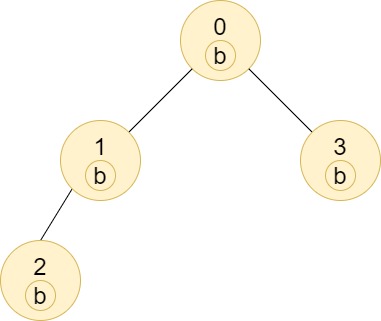
输入：n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb" 输出：[4,2,1,1] 解释：节点 2 的子树中只有节点 2 ，所以答案为 1 。 节点 3 的子树中只有节点 3 ，所以答案为 1 。 节点 1 的子树中包含节点 1 和 2 ，标签都是 'b' ，因此答案为 2 。 节点 0 的子树中包含节点 0、1、2 和 3，标签都是 'b'，因此答案为 4 。
示例 3：
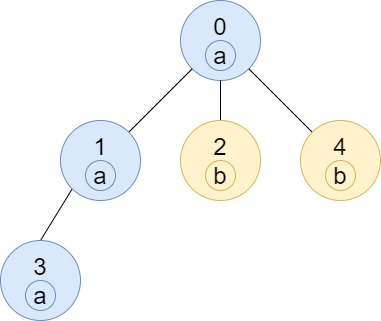
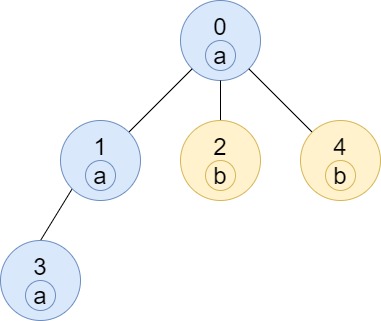
输入：n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab" 输出：[3,2,1,1,1]
示例 4：
输入：n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa" 输出：[1,2,1,1,2,1]
示例 5：
输入：n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa" 输出：[6,5,4,1,3,2,1]
提示：
1 <= n <= 10^5edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != bilabels.length == nlabels仅由小写英文字母组成
class Solution { TreeSet<Integer>[] graph; String labels; int[] ans; public int[] countSubTrees(int n, int[][] edges, String labels) { this.labels = labels; graph = new TreeSet[n]; for (int i = 0; i < n; i++) { graph[i] = new TreeSet<>(); } //无向图，两边一起放 for (int[] edge : edges) { graph[edge[0]].add(edge[1]); graph[edge[1]].add(edge[0]); } ans = new int[n]; dfs(0, new boolean[n]); return ans; } int[] dfs(int root, boolean[] visited) { visited[root] = true; //以root为根节点的子树中每个字母的个数 int[] count = new int[26]; //先统计根节点 count[labels.charAt(root) - 'a']++; for (int next : graph[root]) { if (!visited[next]) { //再统计每个子树 int[] res = dfs(next, visited); for (int i = 0; i < 26; i++) { count[i] += res[i]; } } } //更新结果数组 ans[root] = count[labels.charAt(root)-'a']; return count; } }
给你一个只包含小写字母的字符串 s ，你需要找到 s 中最多数目的非空子字符串，满足如下条件：
- 这些字符串之间互不重叠，也就是说对于任意两个子字符串
s[i..j]和s[k..l]，要么j < k要么i > l。 - 如果一个子字符串包含字符
c，那么s中所有c字符都应该在这个子字符串中。
请你找到满足上述条件的最多子字符串数目。如果有多个解法有相同的子字符串数目，请返回这些子字符串总长度最小的一个解。可以证明最小总长度解是唯一的。
请注意，你可以以 任意 顺序返回最优解的子字符串。
示例 1：
输入：s = "adefaddaccc" 输出：["e","f","ccc"] 解释：下面为所有满足第二个条件的子字符串： [ "adefaddaccc" "adefadda", "ef", "e", "f", "ccc", ] 如果我们选择第一个字符串，那么我们无法再选择其他任何字符串，所以答案为 1 。如果我们选择 "adefadda" ，剩下子字符串中我们只可以选择 "ccc" ，它是唯一不重叠的子字符串，所以答案为 2 。同时我们可以发现，选择 "ef" 不是最优的，因为它可以被拆分成 2 个子字符串。所以最优解是选择 ["e","f","ccc"] ，答案为 3 。不存在别的相同数目子字符串解。
示例 2：
输入：s = "abbaccd" 输出：["d","bb","cc"] 解释：注意到解 ["d","abba","cc"] 答案也为 3 ，但它不是最优解，因为它的总长度更长。
提示：
1 <= s.length <= 10^5s只包含小写英文字母。
class Solution { public List<String> maxNumOfSubstrings(String s) { List<String> ret = new ArrayList<>(); //所有字母的个数 int[] cnt = new int[26]; for(int i=0; i<s.length(); i++) { cnt[s.charAt(i)-'a']++; } //i-左边有效位置，j-右边有效位置 int i=0, j =-1, n = s.length(); //字母第一次出现的位置，字母转化为index Map<Integer, Integer> first = new HashMap<>(); //字母最近一次出现的位置 Map<Integer, Integer> last = new HashMap<>(); while(++j < n) { int index = s.charAt(j)-'a'; cnt[index]--; if(first.get(index) == null) { first.put(index, j); } last.put(index, j); //当前位置某一个字母结束 if(cnt[index] == 0) { //有效子串起始位置为[i,first.get(index)],终止位置为j int start = first.get(index); if(start < i) continue; //从start开始向i扩展，如果找到就停止，即是最短的子串 for( ; start >=i; start--) { boolean valid = true; for(int pos=0; pos<26; pos++) { //没有出现过的字符 if(first.get(pos) == null && last.get(pos) == null) { continue; } //[start,j] 中没有出现的字母 if(last.get(pos) < start) { continue; } // System.out.println(pos + "," + cnt[pos] + "," + last.get(pos)); //两种情况不合条件： //1.[start,j] 中出现的字母，但字母起始位置在start之前。 //2. pos字母没有找完，即j之后还有字母出现 if(first.get(pos) < start || cnt[pos] != 0) { valid = false; break; } } if(valid) { ret.add(s.substring(start, j+1)); i = j+1; break; } } } } return ret; } }
Winston 构造了一个如上所示的函数 func 。他有一个整数数组 arr 和一个整数 target ，他想找到让 |func(arr, l, r) - target| 最小的 l 和 r 。
请你返回 |func(arr, l, r) - target| 的最小值。
请注意， func 的输入参数 l 和 r 需要满足 0 <= l, r < arr.length 。
示例 1：
输入：arr = [9,12,3,7,15], target = 5 输出：2 解释：所有可能的 [l,r] 数对包括 [[0,0],[1,1],[2,2],[3,3],[4,4],[0,1],[1,2],[2,3],[3,4],[0,2],[1,3],[2,4],[0,3],[1,4],[0,4]]， Winston 得到的相应结果为 [9,12,3,7,15,8,0,3,7,0,0,3,0,0,0] 。最接近 5 的值是 7 和 3，所以最小差值为 2 。
示例 2：
输入：arr = [1000000,1000000,1000000], target = 1 输出：999999 解释：Winston 输入函数的所有可能 [l,r] 数对得到的函数值都为 1000000 ，所以最小差值为 999999 。
示例 3：
输入：arr = [1,2,4,8,16], target = 0 输出：0
提示：
1 <= arr.length <= 10^51 <= arr[i] <= 10^60 <= target <= 10^7
就这个题，我感觉写到天黑我也写不出来，😔
class Solution { //这个题我读了半天代码才勉强能读懂，位运算太蒙了 public int closestToTarget(int[] arr, int target) { // System.out.println(4>>1); int m = 20; int n = arr.length; int[][] prev = new int[m][n]; //prev[i][j]代表arr[j]右移i位为0的最大的 for(int i = 0; i < m; i++){ for(int j = 0; j < n; j++){ if(j == 0){ prev[i][j] = -1; }else{ prev[i][j] = prev[i][j - 1]; } if(get(arr[j], i) == 0){ prev[i][j] = j; } } } int ans = Integer.MAX_VALUE; for(int i = 0; i < n; i++){ //从i=j开始模拟 int val = arr[i]; int j = i; ans = Math.min(ans, Math.abs(val - target)); while(j >= 0){ int last = -1; for(int k = 0; k < m; k++){ //&运算符只能减小 //如果val右移k位，最后一位为0，可以跳过了 //最后一位为0，&运算完，那一位也变成0了 //其实总体来说就是 //几个相邻的数&运算完不变需要做一些跳过的处理，减少不必要的& if(get(val, k) == 0){ continue; } //arr[j]这个数最多右移k位的数的下标 last = Math.max(last, prev[k][j]); } j = last; if(j >= 0){ //val算上当前的值 val &= arr[j]; ans = Math.min(ans, Math.abs(val - target)); } } } return ans; } //二进制向右移动i位，就是二进制的最后i位删掉 //然后看那个树的最后一位是不是1 public int get(int x, int i){ return (x >> i) & 1; } }
