Java实现 LeetCode第197场周赛 (题号5460,5461,5211,5463)
给你一个整数数组 nums 。
如果一组数字 (i,j) 满足 nums[i] == nums[j] 且 i < j ,就可以认为这是一组 好数对 。
返回好数对的数目。
示例 1:
输入:nums = [1,2,3,1,1,3] 输出:4 解释:有 4 组好数对,分别是 (0,3), (0,4), (3,4), (2,5) ,下标从 0 开始
示例 2:
输入:nums = [1,1,1,1] 输出:6 解释:数组中的每组数字都是好数对
示例 3:
输入:nums = [1,2,3] 输出:0
提示:
1 <= nums.length <= 1001 <= nums[i] <= 100
1 class Solution { 2 public int numIdenticalPairs(int[] nums) { 3 int count = 0; 4 for (int i=0;i<nums.length;i++){ 5 for (int j=i+1;j<nums.length;j++){ 6 if(nums[i]==nums[j]){ 7 ++count; 8 } 9 } 10 } 11 return count; 12 } 13 }

又找到了一种简单方法
1 class Solution { 2 //一个数出现了n次的话,这个数的好数对就是n*(n-1)/2 3 public int numIdenticalPairs(int[] nums) { 4 5 int[] temp = new int[101]; 6 for(int i:nums){ 7 ++temp[i]; 8 } 9 int count=0; 10 for(int i:temp){ 11 if(i==0){ 12 continue; 13 }else{ 14 count+=(i*(i-1)/2); 15 } 16 } 17 return count; 18 19 20 21 } 22 }

给你一个二进制字符串 s(仅由 '0' 和 '1' 组成的字符串)。
返回所有字符都为 1 的子字符串的数目。
由于答案可能很大,请你将它对 10^9 + 7 取模后返回。
示例 1:
输入:s = "0110111" 输出:9 解释:共有 9 个子字符串仅由 '1' 组成 "1" -> 5 次 "11" -> 3 次 "111" -> 1 次
示例 2:
输入:s = "101" 输出:2 解释:子字符串 "1" 在 s 中共出现 2 次
示例 3:
输入:s = "111111" 输出:21 解释:每个子字符串都仅由 '1' 组成
示例 4:
输入:s = "000" 输出:0
提示:
s[i] == '0'或s[i] == '1'1 <= s.length <= 10^5
1 class Solution { 2 //这个题得思路是找到1得多少个子串 3 //如果6个1:字串得数量为6+5+4+3+2+1 4 /* 5 一位字串:6 6 两位字串:5个,从开始走假设六位数为123456 7 12 23 34 45 56 8 每两位猜错一个,到最后一个正好比1位字串少一个 9 三位字串:4个 123 234 345 456 一样的 10 11 */ 12 13 public int numSub(String s) { 14 String[] strs = s.split("0"); 15 int[] num = new int [100000+1]; 16 //先按照0分解,看看每一块1都有多少位 17 for (String ss:strs){ 18 ++num[ss.length()]; 19 } 20 int res = 0; 21 //从1位开始,0位是不作数得 22 for (int i=1;i<num.length;i++){ 23 if(num[i]==0) continue;i 24 //如果是奇数就 25 //例子: 26 //你可以带进去,相当于高斯求和得意思 27 // (i+1)/2*i *num[i] 28 // 下面我写的可能很繁琐,其实就是为了取余防止超 29 if((i&1)==1){ 30 long temp = ((i+1)/2)%1000000007l*i; 31 temp=temp%1000000007*num[i]%1000000007; 32 res=(res+(int)temp)%1000000007; 33 } else{ 34 //你可以带进去,相当于高斯求和得意思 35 //(i+1)/2*i*num[i] 36 long temp = (i+1)%1000000007l*i/2%1000000007; 37 38 temp=temp%1000000007*num[i]%1000000007; 39 res=(res+(int)temp)%1000000007; 40 41 } 42 } 43 return res; 44 } 45 }

给你一个由 n 个节点(下标从 0 开始)组成的无向加权图,该图由一个描述边的列表组成,其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边,且该边遍历成功的概率为 succProb[i] 。
指定两个节点分别作为起点 start 和终点 end ,请你找出从起点到终点成功概率最大的路径,并返回其成功概率。
如果不存在从 start 到 end 的路径,请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ,就会被视作正确答案。
示例 1:

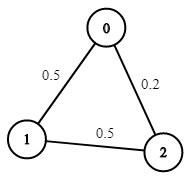
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2 输出:0.25000 解释:从起点到终点有两条路径,其中一条的成功概率为 0.2 ,而另一条为 0.5 * 0.5 = 0.25
示例 2:
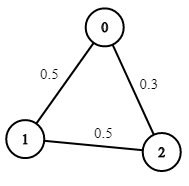
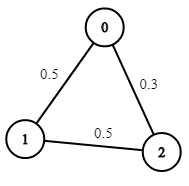
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2 输出:0.30000
示例 3:
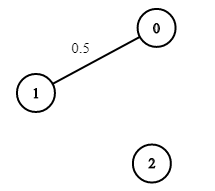
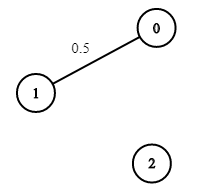
输入:n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2 输出:0.00000 解释:节点 0 和 节点 2 之间不存在路径
提示:
2 <= n <= 10^40 <= start, end < nstart != end0 <= a, b < na != b0 <= succProb.length == edges.length <= 2*10^40 <= succProb[i] <= 1- 每两个节点之间最多有一条边
1 class Solution { 2 3 public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) { 4 5 double error = 1e-6; 6 Map<Integer, List<Node>> map = new HashMap<>(); 7 //把当前得结构放进去 8 for (int i = 0; i < edges.length; i++) { 9 int[] e = edges[i]; 10 if (!map.containsKey(e[0])) { 11 map.put(e[0], new ArrayList<>()); 12 } 13 14 if (!map.containsKey(e[1])) { 15 map.put(e[1], new ArrayList<>()); 16 } 17 //这里是无向图,要正反放入 18 map.get(e[0]).add(new Node(e[0], e[1], succProb[i])); 19 map.get(e[1]).add(new Node(e[1], e[0], succProb[i])); 20 } 21 double[] dp = new double[n]; 22 dp[start] = 1; 23 //BFS搜索 24 Queue<Integer> q = new ArrayDeque<>(); 25 q.add(start); 26 while (!q.isEmpty()) { 27 int cur = q.poll(); 28 //找到以当前结点连接得点 29 for (Node node : map.getOrDefault(cur, new ArrayList<>())) { 30 //循环,看看能不能让成功率更高,如果成功率更高,就可以选用, 31 //把点放入node 32 if (dp[cur] * node.prob > dp[node.to] + error) { 33 q.add(node.to); 34 //保存当前点得成功率 35 dp[node.to] = dp[cur] * node.prob; 36 } 37 } 38 } 39 return dp[end]; 40 } 41 42 class Node { 43 int from; 44 int to; 45 double prob; 46 public Node(int from, int to, double prob) { 47 this.from = from; 48 this.to = to; 49 this.prob = prob; 50 } 51 } 52 }

一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标,并希望能够以此为依据为新的服务中心选址:使服务中心 到所有客户的欧几里得距离的总和最小 。
给你一个数组 positions ,其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置,返回到所有客户的 欧几里得距离的最小总和 。
换句话说,请你为服务中心选址,该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值:
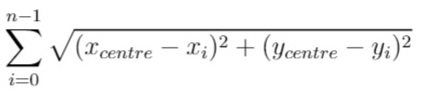
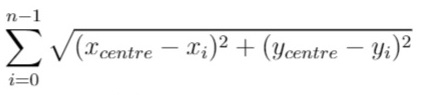
与真实值误差在 10^-5 之内的答案将被视作正确答案。
示例 1:
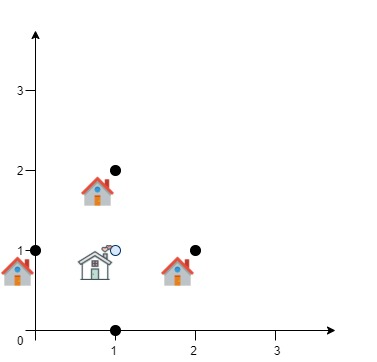
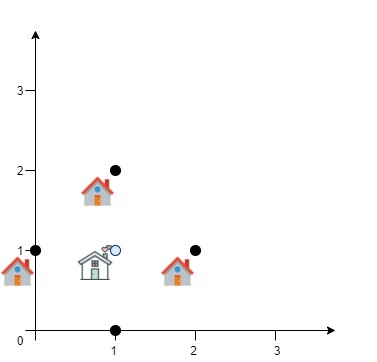
输入:positions = [[0,1],[1,0],[1,2],[2,1]] 输出:4.00000 解释:如图所示,你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置,这样一来到每个客户的距离就都是 1,所有距离之和为 4 ,这也是可以找到的最小值。
示例 2:
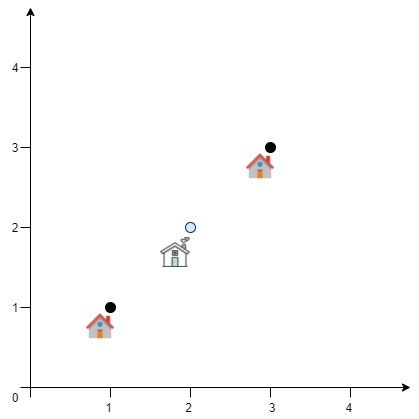
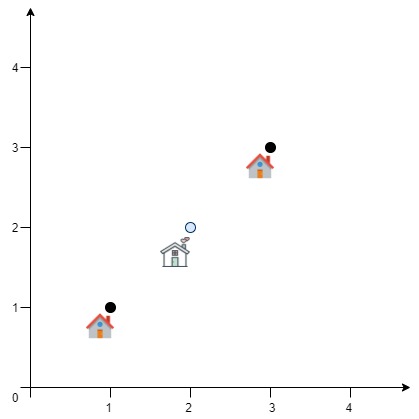
输入:positions = [[1,1],[3,3]] 输出:2.82843 解释:欧几里得距离可能的最小总和为 sqrt(2) + sqrt(2) = 2.82843
示例 3:
输入:positions = [[1,1]] 输出:0.00000
示例 4:
输入:positions = [[1,1],[0,0],[2,0]] 输出:2.73205 解释:乍一看,你可能会将中心定在 [1, 0] 并期待能够得到最小总和,但是如果选址在 [1, 0] 距离总和为 3 如果将位置选在 [1.0, 0.5773502711] ,距离总和将会变为 2.73205 当心精度问题!
示例 5:
输入:positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]] 输出:32.94036 解释:你可以用 [4.3460852395, 4.9813795505] 作为新中心的位置
提示:
1 <= positions.length <= 50positions[i].length == 20 <= positions[i][0], positions[i][1] <= 100
1 class Solution { 2 //这个题当时周赛没做出来,思路很新颖,又学习到了 3 public double getMinDistSum(int[][] positions) { 4 //先用所有点把最平均得那个点求出来 5 double[] current_point = new double[2]; 6 for (int i = 0; i < positions.length; i++) { 7 current_point[0] += positions[i][0]; 8 current_point[1] += positions[i][1]; 9 } 10 current_point[0] /= positions.length; 11 current_point[1] /= positions.length; 12 //求出最平均得点,到所有点得距离 13 double minimum_distance = distSum(current_point, positions, positions.length); 14 //迪杰斯特拉,看看那个点会比当前点更近距离 15 int k = 0; 16 while (k < positions.length) { 17 //这里不能是当前点,k为循环的点,如果相等的话,说明有相同的点 18 for (int i = 0; i < positions.length && i != k; i++) { 19 double[] newpoint = new double[2]; 20 newpoint[0] = positions[i][0]; 21 newpoint[1] = positions[i][1]; 22 double newd = distSum(newpoint, positions, positions.length); 23 if (newd < minimum_distance) { 24 minimum_distance = newd; 25 current_point[0] = newpoint[0]; 26 current_point[1] = newpoint[1]; 27 } 28 } 29 k++; 30 } 31 //然后就是通过一点一点得找到更近得点 32 double test_distance = 1000; 33 int flag = 0; 34 //四个方向 35 double[][] test_point = { { -1.0, 0.0 }, { 0.0, 1.0 }, { 1.0, 0.0 }, { 0.0, -1.0 } }; 36 //当距离小于0.0001的时候,就认为就是最短点了 37 while (test_distance > 0.0001) { 38 flag = 0; 39 for (int i = 0; i < 4; i++) { 40 double[] newpoint = new double[2]; 41 //四个方向去找 42 newpoint[0] = current_point[0] + (double) test_distance * test_point[i][0]; 43 newpoint[1] = current_point[1] + (double) test_distance * test_point[i][1]; 44 double newd = distSum(newpoint, positions, positions.length); 45 if (newd < minimum_distance) { 46 //如果有更近得点说明找对了方向,此次循环就可以跳过去了 47 minimum_distance = newd; 48 current_point[0] = newpoint[0]; 49 current_point[1] = newpoint[1]; 50 flag = 1; 51 break; 52 } 53 } 54 if (flag == 0) 55 test_distance /= 2; 56 } 57 return minimum_distance; 58 } 59 //求某个点到所有点得和 60 double distSum(double[] p, int[][] arr, int n) { 61 double sum = 0; 62 for (int i = 0; i < n; i++) { 63 double distx = Math.abs(arr[i][0] - p[0]); 64 double disty = Math.abs(arr[i][1] - p[1]); 65 sum += Math.sqrt((distx * distx) + (disty * disty)); 66 } 67 68 return sum; 69 } 70 }