软件工程实践2019第三次作业
准备工作阶段
1,创建好Github库后传输文件,Github项目地址(https://github.com/leee329/031702339)
2,并按要求安置好Visual Stdio 2017并做好相关文件夹
3.PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 40 | 40 |
| Estimate | 估计这个任务需要多少时间 | 10 | 15 |
| Development | 开发 | 120 | 120 |
| Analysis | 需求分析 (包括学习新技术) | 120 | 90 |
| Design Spec | 生成设计文档 | 20 | 30 |
| Design Review | 设计复审 | 5 | 5 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 60 | 120 |
| Design | 具体设计 | 20 | 30 |
| Coding | 具体编码 | 120 | 180 |
| Code Review | 代码复审 | 30 | 15 |
| Test | 测试(自我测试,修改代码,提交修改) | 60 | 300 |
| Reporting | 报告 | 30 | 45 |
| Test Repor | 测试报告 | 30 | 40 |
| Size Measurement | 计算工作量 | 15 | 30 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 60 | 70 |
| 合计 | (自闭时长) | 740 | 1130 |
没错,因为回溯函数的一个等号我debug了5个小时,一共耗时1130分钟=18h50m,自闭.jpg
开始阶段
1,思考阶段
一开始看到这个题目,我寻思从三宫格往外扩展,实在是太麻烦了,因为实现完三宫格之后,空间还要再扩张,那个时候代码对于新的空间扩张就需要很大的改动,不如直接就从九宫格下手,对于九宫格来说,我得从合法性和唯一性函数以及回溯性函数来进展,其中合法性函数用于判断某个数字在某个位置的合法性,唯一性函数用于判断某个数在某一行/列/宫上的某个位置是否是唯一合法的,回溯函数也就是深度优先搜索函数,用于尝试填充
2,算法关键:三大函数
计算模块接口的设计与实现过程:
合法性函数F1:判定某个数n在某个位置(x,y)的合法性:需要考虑到,如果x所在的这一行,y所在的这一列(x,y),n所在的这一宫全都没有n,就是合法的。
需要考量以(x,y)为中心的十字,和一个九宫格,共21个位置(画图工具真难用):
例如:如图,5在4行4列上,如果第4行和第4列和第5宫都没有5,那么5在这里就算合法的。

唯一性函数F2:先说小函数f:对于每一个数,在每一个位置都进行唯一性判断,判定某个数n,在某行或者某列或者某宫是否是唯一合法的(这一行/列/宫的其他地方都没有n的容身之地):如果合法就填上,需要对n所在的行和列个宫的另外21个数,需要遍历21X21次。
再说大函数F,因为每次填充都会为下一次填充提供新的条件,因此一次的f是不够的,因为f之后又有新条件了,所以f得循环下去,但如果在其中一次f中,没有进行填充操作,F就该结束了
例如:5在4行4列上,如果这一行(4行)中,只有(4,9)5是合法的,那么5在第四行上就算唯一的,如果在第四行上有两个位置是合法的,那么它就不是唯一的了,如果它在(2,2)号宫里只有(5,5)是合法的,那么对于这一宫,它也是唯一的
因此(4,9)和(5,5)将会填入5

试探性函数F3:因为唯一性函数以后,仍然有空位(低级题可以过,高级题仍然有空位),也就是说剩下来的所有数,在所有位置上都是不唯一的,试探性函数也就是一种回溯函数,如果这个数目前来说是合法的,就填下去,但是如果后续有数因为它的填入而无处安放,我就把这个数取出来,换另一个数。
我试着用结构体记下位置和数值供以后返回,无果,我试着用二维来定位一个位置,无果,于是我将一维来定制,比如42,对应着横坐标42/9=4,纵坐标42%9=6
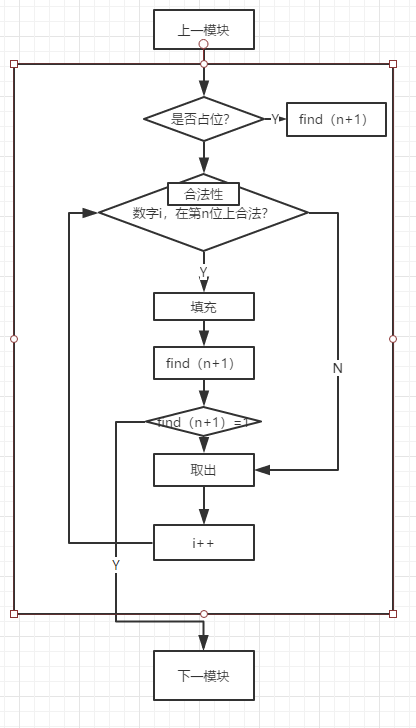
在进行唯一性函数填充以后,我从0开始试探性函数,如果被占据,直接到1,如果1在位置1上不合法,就看2。。。如果3合法,就把3填入1号位后进入2号位试探,如果2号位1-9全都不合法,回退到1号位把3拿出来,进行4的试探。。。直到第80号位都没有出现不合法问题,就结束试探性函数。有点难解释,直接上图,序号表示程序顺序。
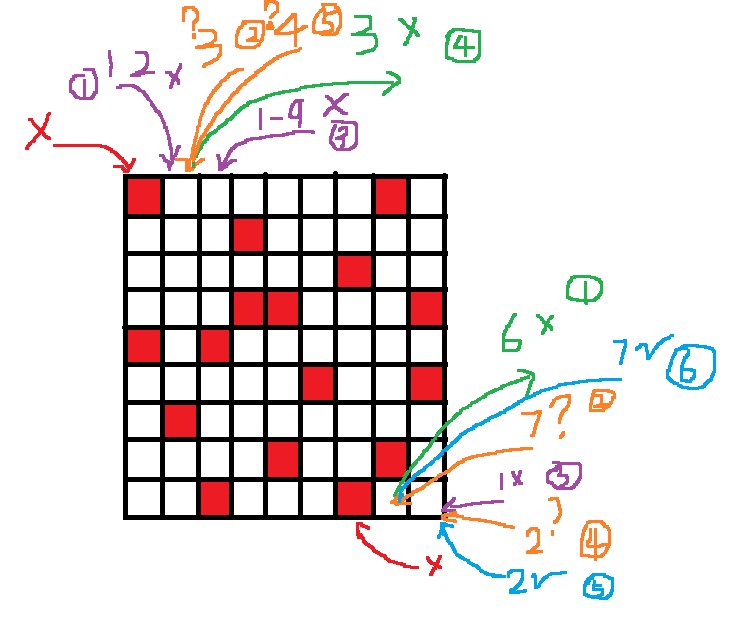
独到之处:通过将唯一性函数与试探性函数结合在一起,达到降低CPU消耗的效果,具体在后面大的算法改进和性能分析。
流程图如下

在这样的结构下,无论是3宫格还是456789宫格,都是适用的
3,模块间的关系以及计算模块部分单元测试展示:
(siz,gl,gw分别是数独规格和宫格规格,因此如下三个函数是针对多种数独的求解方案)
单元测试与模块结合:
对于F1,直接对一个题目遍历一遍就能看出测试是否出问题。
对于F2,在F1没问题的情况下,再将1-9对81个位置进行判断。
对于F3,和F2情况类似,因为F3和F2没有什么关系。
具体单元测试与模块结合如下。
合法性函数:
模块关系:这是最基本的模块,所以它没有被其他模块调用:
Locate错误:占位不合法。
HL错误:行列不合法。
GG错误:宫不合法。
1 bool judge(int x, int y, int num)//坐标和数字 2 { 3 int i, j, t = 0, x1, y1; 4 if (gl != 0)//如果有宫 5 x1 = x / gl, y1 = y / gw;//宫坐标转换 6 if (sd[x][y] == 0)//进行位置判断,对应下图的LOCATE错误 7 { 8 for (i = 0; i < siz; i++) 9 if (sd[x][i] == num || sd[i][y] == num)//进行十字判断,对应下图的HL型错误 10 return 0; 11 if (gl != 0) 12 { 13 for (i = x1 * gl; i < x1*gl + gl; i++)//进行宫判断,对应下图GG型错误 14 for (j = y1 * gw; j < y1*gw + gw; j++) 15 if (sd[i][j] == num) 16 return 0; 17 } 18 return 1;//对应下图的成功提示 19 } 20 else 21 return 0; 22 }
测试方法:
for(k=0;k<siz;k++)//siz是规格 for (i = 0; i < siz; i++) for (j = 0; j < siz; j++) judge(i,j,k);
测试数据覆盖的代码有如上代码和数据输入输出代码。
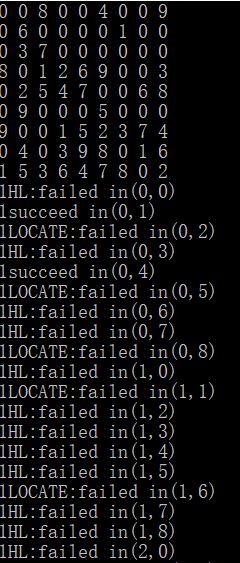
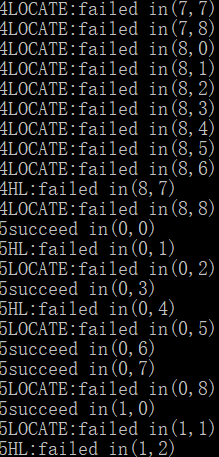
唯一性函数:
模块关系/测试思路,如下:
测试数据输入到sd[][]后,就到达了图中的“上一模块”,然后直接调用即可

测试数据覆盖的代码除了如下代码以外,还有合法性函数的代码,和数据输入输出代码。
1 void single()//唯一性 2 { 3 int i, j, k, l, m, t = 0, x0 = 0, y0 = 0, flag, p = 1;; 4 while (1) 5 { 6 flag = 0; 7 for (i = 1; i <= siz; i++)//对每一个数字进行唯一性判断 8 { 9 for (j = 0; j < siz; j++) 10 { 11 t = 0; x0 = 0; y0 = 0; 12 for (k = 0; k < siz; k++)//在某行的唯一性 13 { 14 t = t + judge(j, k, i); 15 if (judge(j, k, i)) 16 x0 = j, y0 = k; 17 } 18 if (t == 1)//对于行的位置上填充 19 { 20 sd[x0][y0] = i; 21 flag++; 22 } 23 t = 0; x0 = 0; y0 = 0; 24 for (k = 0; k < siz; k++)//在某列的唯一性 25 { 26 t = t + judge(k, j, i); 27 if (judge(k, j, i)) 28 x0 = k, y0 = j; 29 } 30 if (t == 1)//对应列上的填充 31 { 32 sd[x0][y0] = i; 33 flag++; 34 } 35 } 36 if (gl != 0) 37 { 38 for (j = 0; j < gl; j++) 39 { 40 for (k = 0; k < gw; k++)//x在某宫的唯一性 41 { 42 t = 0; x0 = 0; y0 = 0; 43 for (l = gl * j; l < gl*j + gl; l++) 44 for (m = gw * k; m < gw*k + gw; m++) 45 { 46 t = t + judge(l, m, i); 47 if (judge(l, m, i)) 48 x0 = l, y0 = m; 49 } 50 if (t == 1)//填充 51 { 52 sd[x0][y0] = i; 53 flag++; 54 } 55 } 56 } 57 } 58 } 59 if (flag == 0) 60 break; 61 } 62 }
测试方法:直接调用
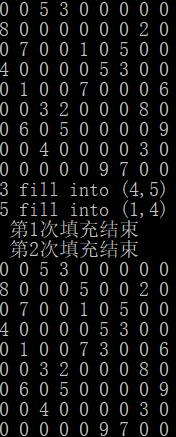

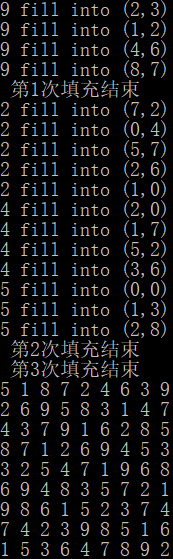
可以看出,简单一点的数独,都可以用唯一性函数做完,复杂一点的,需要用回溯法解决。
试探性函数:
模块关系/测试思路如下:
测试数据输入到sd[][]后,就到达了图中的“上一模块”,然后直接调用即可
测试数据覆盖的代码除了如下代码以外,还有合法性函数的代码,和数据输入输出代码。
1 int find(int s) 2 { 3 int x = s / siz, y = s % siz, n; 4 if (s > siz*siz - 1) 5 return 1; 6 7 if (sd[x][y] != 0)//每次探索都检查有没有占位 8 return (find(s + 1)); 9 else 10 { 11 for (n = 1; n <= siz; n++) 12 { 13 if (judge(x, y, n))//判断成功 14 { 15 sd[x][y] = n;//先填充 16 if (find(s + 1))//继续探索 17 return 1; 18 } 19 sd[x][y] = 0;//后取出 20 } 21 } 22 return 0; 23 }
测试方法:直接调用
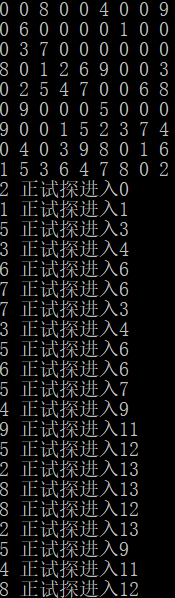
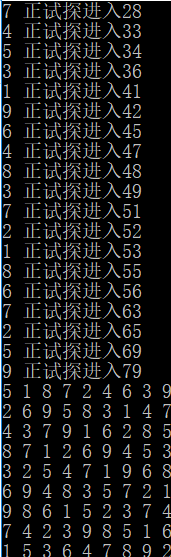
4,算法/性能改进:
改进大概花费了3小时,对于试探性函数,算法的时间复杂度是O(n2n+1),对于唯一性函数算法的时间复杂度是O(n5),显然唯一性函数会比试探性函数来的好
因此每多一个不确定的空位,试探性函数的工作时间都要增加很多,所以我放弃了一开始的只有合法性和试探性函数的结构,中间加个唯一性函数来为试探性函数减少工作时间:
VS 2017 性能测试结果如下,对于CPU占用率:
简单题:
2 0 0 0 0 0 0 0 0 0 0 6 3 0 0 0 7 0 5 0 0 0 0 0 1 0 0 9 6 7 4 0 0 0 0 5 8 1 3 0 0 0 0 0 0 4 2 0 7 1 8 9 6 3 3 5 0 0 4 1 6 9 7 6 9 8 2 7 3 5 4 1 0 4 0 0 5 9 2 0 8
进行唯一性和试探性求解:
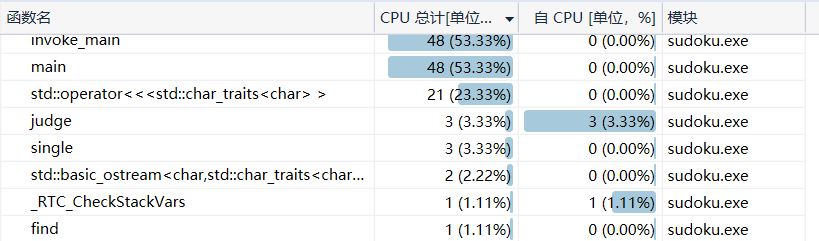
只进行试探性求解:
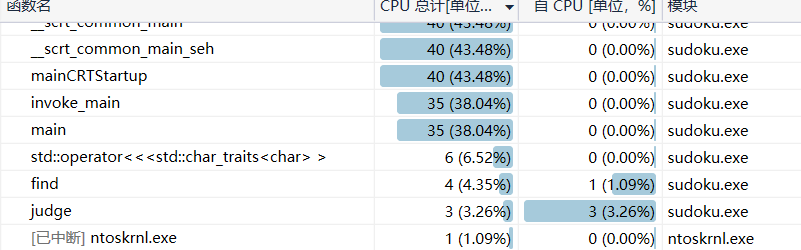
困难题:
0 0 0 0 0 0 0 0 0 5 6 4 1 0 0 0 0 0 0 0 8 0 0 0 0 6 0 1 0 0 0 8 4 7 5 0 0 0 0 2 7 0 0 0 0 7 0 0 0 0 3 1 2 0 0 0 3 0 0 0 0 7 9 0 0 7 0 0 8 0 3 0 0 9 0 0 3 0 6 0 0
进行唯一性和试探性求解:
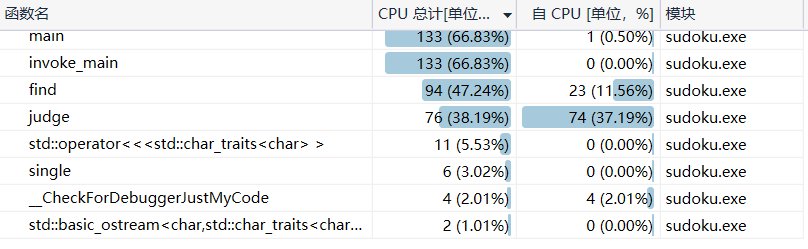
只进行试探性求解:
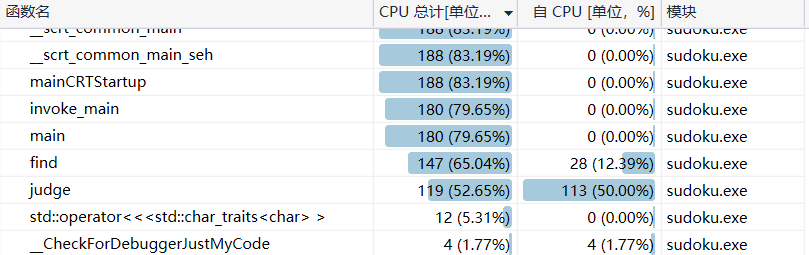
对比可以发现,双函数联合求解与单一试探性求解在
简单难度下的时候:
性能差别不大,有时甚至后者更优,比如图中,唯一性函数用了3个单位的CPU使用量,才让试探性的CPU使用量降低1个单位,指标上降低1个百分点
总体上性能的CPU使用量都为40多,其他简单题的测试样例也都是40-60以内,其中两种求解方案也是不相上下;
困难难度下的时候:
性能差距拉大,前者秒杀后者:唯一性函数仅用了6个单位的CPU使用量,就将试探性函数占用的CPU大幅降低了53个单位,指标上降低27个百分点
总体性能上,差距大都由试探性函数拉开,其他困难题目的测试样例也是如此,困难题目的CPU使用量浮动较大不便统计,一般在200±50,但都是双函数联合求解的方式明显取胜
5,异常处理
对命令行参数的异常处理,针对了总参数,和数独规格处理
if(argc!=9) { cout<<"总参数错误"; return 0; } else { if(siz>9||siz<3) { cout<<"规格参数错误"; return 0; } }
对最后求解完的数独做异常处理,如果仍有空位,就会出现数独错误
for(k=0;k<time;k++)//容错性 { for(i=0;i<siz;i++) for(j=0;j<siz;j++) if(da[k][i][j]==0) cout<<"数独错误"; }
(siz是数独规格,gl和gw是宫的长和宽)
6,总程序
在主函数中进行参数的解析和文件的打开->读取->求解->写入->关闭操作,其中读取求解是多次循环,因为不止一个数独。
#include "stdafx.h" #include<stdio.h> #include<stdlib.h> #include<iostream> #include<string.h> #pragma warning(disable:4996) using namespace std; int sd[90][90], siz, gl, gw, time, da[10][90][90]; bool judge(int x, int y, int num) { int i, j, t = 0, x1, y1; if (gl != 0) x1 = x / gl, y1 = y / gw; if (sd[x][y] == 0) { for (i = 0; i < siz; i++) if (sd[x][i] == num || sd[i][y] == num) return 0; if (gl != 0) { for (i = x1 * gl; i < x1*gl + gl; i++) for (j = y1 * gw; j < y1*gw + gw; j++) if (sd[i][j] == num) return 0; } return 1; } else return 0; } void single() { int i, j, k, l, m, t = 0, x0 = 0, y0 = 0, flag, p = 1;; while (1) { flag = 0; for (i = 1; i <= siz; i++) { for (j = 0; j < siz; j++) { t = 0; x0 = 0; y0 = 0; for (k = 0; k < siz; k++) { t = t + judge(j, k, i); if (judge(j, k, i)) x0 = j, y0 = k; } if (t == 1) { sd[x0][y0] = i; flag++; } t = 0; x0 = 0; y0 = 0; for (k = 0; k < siz; k++) { t = t + judge(k, j, i); if (judge(k, j, i)) x0 = k, y0 = j; } if (t == 1) { sd[x0][y0] = i; flag++; } } if (gl != 0) { for (j = 0; j < gl; j++) { for (k = 0; k < gw; k++) { t = 0; x0 = 0; y0 = 0; for (l = gl * j; l < gl*j + gl; l++) for (m = gw * k; m < gw*k + gw; m++) { t = t + judge(l, m, i); if (judge(l, m, i)) x0 = l, y0 = m; } if (t == 1) { sd[x0][y0] = i; flag++; } } } } } if (flag == 0) break; } } int find(int s) { int x = s / siz, y = s % siz, n; if (s > siz*siz - 1) return 1; if (sd[x][y] != 0) return (find(s + 1)); else { for (n = 1; n <= siz; n++) { if (judge(x, y, n)) { sd[x][y] = n; if (find(s + 1)) return 1; } sd[x][y] = 0; } } return 0; } int main(int argc, char *argv[]) { FILE* fp; int i, j, k, l, m, t = 0, x0 = 0, y0 = 0; char *x; char *y; for (i = 0; i < argc; i++)//参数读取 { if (strlen(argv[i]) == 1) { if (i == 2) siz = atoi(argv[i]);//读取规格 if (i == 4) time = atoi(argv[i]);//读取数独个数 } if(i==6) x=argv[i]; if(i==8) y=argv[i]; } if (siz % 3 == 0)//宫的规格的转化 { gl = siz / 3; if (gl != 0) gw = siz / gl; } if (siz % 2 == 0) { gl = siz / 2; if (gl != 0) gw = siz / gl; } if(siz==6) gl=2,gw=3; if(argc!=9) { cout<<"总参数错误"; return 0; } else { if(siz>9||siz<3) { cout<<"规格参数错误"; return 0; } } fp = fopen(x, "r");//文件读取 if (fp == NULL) //为空时返回错误 return -1; for (k = 0; k < time; k++) { i = 0; j = 0; while (i != siz) //将每一个数独划开 { fscanf(fp, "%d", &sd[i][j]); j++; if (j == siz) { j = 0; i++; } } single(); t = find(0); for (i = 0; i < siz; i++) for (j = 0; j < siz; j++) da[k][i][j] = sd[i][j];//解决后存入da三维数组 } fclose(fp); fp = fopen(y, "w"); if (fp == NULL) return -1; for (k = 0; k < time; k++) { for (i = 0; i < siz; i++) { for (j = 0; j < siz; j++) { fprintf(fp, "%d", da[k][i][j]);//依次递交 if (j != siz - 1) fprintf(fp, " "); } if (i != siz - 1) fprintf(fp, "\n"); } if (k != time - 1) fprintf(fp, "\n\n"); } fclose(fp); for(k=0;k<time;k++)//容错性 { for(i=0;i<siz;i++) for(j=0;j<siz;j++) if(da[k][i][j]==0) cout<<"数独错误"; } return 0; }
测试:
例1:
E:\软工\031702339\Sudoku\Sudoku>Sudoku.exe -m 9 -n 2 -i input.txt -o output.txt


例2:
E:\软工\031702339\Sudoku\Sudoku>Sudoku.exe -m 3 -n 1 -i input.txt -o output.txt

例3:
E:\软工\031702339\Sudoku\Sudoku>Sudoku.exe -m 8 -n 2 -i input.txt -o output.txt


例456789:
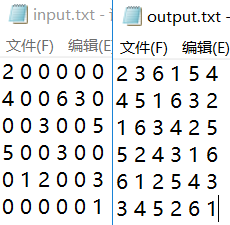


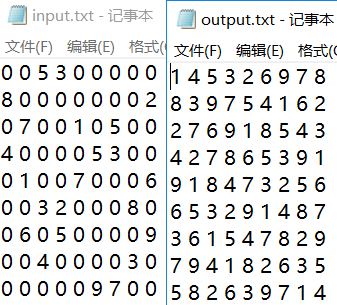


例10(异常):

总结:一步一步过来,遇到了很多问题,所以也确确实实学习到了很多,学到了Github的文件上传,VS性能测试,VS的E0266,C4996,LNK2019,LNK2005,C2085等等各种奇葩报错或警告的解决办法,还有函数定制的方式改善,还有文件传输的具体规范等等很多很多,同时也意识到项目制定的规范性。
面对这些问题,有的绕开了,有的迎难而上,这样的处理方式不由得令我反观试探性函数,我不正如它一样不断的寻错,不断的改进吗?
好啦,为期20h的周常自闭结束。容错性函数或将改善。