PTA 数据结构 哈夫曼树与哈夫曼编码
题目描述
题目背景:介绍什么是哈夫曼树和哈夫曼编码, 不影响做题
哈夫曼树(Huffman Tree)又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。
在数据通信中,需要将传送的文字转换成二进制的字符串,用0,1码的不同排列来表示字符。例如,需传送的报文为“AFTER DATA EAR ARE ART AREA”,这里用到的字符集为“A,E,R,T,F,D”,各字母出现的次数为{8,4,5,3,1,1}。现要求为这些字母设计编码。要区别6个字母,最简单的二进制编码方式是等长编码,固定采用3位二进制,可分别用000、001、010、011、100、101对“A,E,R,T,F,D”进行编码发送,当对方接收报文时再按照三位一分进行译码。显然编码的长度取决报文中不同字符的个数。若报文中可能出现26个不同字符,则固定编码长度为5。然而,传送报文时总是希望总长度尽可能短。在实际应用中,各个字符的出现频度或使用次数是不相同的,如A、B、C的使用频率远远高于X、Y、Z,自然会想到设计编码时,让使用频率高的用短码,使用频率低的用长码,以优化整个报文编码。
为使不等长编码为前缀编码(即要求一个字符的编码不能是另一个字符编码的前缀),可用字符集中的每个字符作为叶子结点生成一棵编码二叉树,为了获得传送报文的最短长度,可将每个字符的出现频率作为字符结点的权值赋予该结点上,显然字使用频率越小权值越小,权值越小叶子就越靠下,于是频率小编码长,频率高编码短,这样就保证了此树的最小带权路径长度效果上就是传送报文的最短长度。因此,求传送报文的最短长度问题转化为求由字符集中的所有字符作为叶子结点,由字符出现频率作为其权值所产生的哈夫曼树的问题。利用哈夫曼树来设计二进制的前缀编码,既满足前缀编码的条件,又保证报文编码总长最短。
本题要求从键盘输入若干电文所用符号及其出现的频率,然后构造哈夫曼树,从而输出哈夫曼编码。
注意:为了保证得到唯一的哈夫曼树,本题规定在构造哈夫曼树时,左孩子结点权值不大于右孩子结点权值。如权值相等,则先选优先级队列中先出队的节点。编码时,左分支取“0”,右分支取“1”。
输入格式
输入有3行
第1行:符号个数n(2~20)
第2行:一个不含空格的字符串。记录着本题的符号表。我们约定符号都是单个的小写英文字母,且 从字符‘a’开始顺序出现。也就是说,如果 n 为 2 ,则符号表为 ab ;如果 n 为 6,则符号为 abcdef;以此类推。
第3行:各符号出现频率(用乘以100后的整数),用空格分隔。
输出格式
先输出构造的哈夫曼树带权路径长度。 接下来输出n行,每行是一个字符和该字符对应的哈夫曼编码。字符按字典顺序输出。字符和哈夫曼编码之间以冒号分隔。
样例
输入:
8
abcdefgh
5 29 7 8 14 23 3 11
输出:
271
a:0001
b:10
c:1110
d:1111
e:110
f:01
g:0000
h:001
一点说明
关于题目描述中的"如权值相等,则先选优先级队列中先出队的节点"
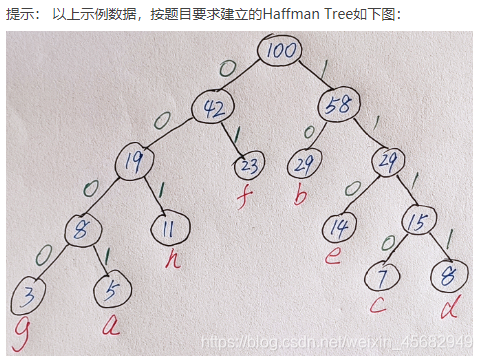
可以参考上图, 权值为7的节点选择了权值为8的叶子节点, 而不是权值为8的子树
感觉题目想表达的意思是, 若权值相等,则先选优先级队列中先入队的节点
(如有错误, 望指正)
想法
利用优先队列维护小根堆(因为建树时,要选两个权值最小的),
利用哈夫曼算法建树,
再根据所建哈夫曼树,利用深搜回溯,得到各个字符的哈夫曼编码和树的带权路径长度
实现
#include <cstdio>
#include <iostream>
#include <string>
#include <queue>
#include <vector>
using namespace std;
struct node
{
int weight;
char ch = 'z' + 1; // 这样在优先队列自定义排序时, 可以做到权值相等,则先选优先级队列中先出队的节点
node *lchild, *rchild;
};
// 自定义优先队列的排序方式, 权值小优先, 权值相等,则先选优先级队列中先出队的节点
struct cmp
{
bool operator() (node* a, node* b)
{
if(a->weight == b->weight)
return a->ch > b->ch;
return a->weight > b->weight;
}
};
int n, WPL; // n:结点数 WPL:树的带权路径长度(非叶子节点的权值和)
string str;
priority_queue<node, vector<node*>, cmp> q; //
vector<char> ans[100]; // 存放哈夫曼编码
vector<char> code; // 用于深搜得到哈夫曼编码
node* createTree() // 建立哈夫曼树
{
node* r;
while(!q.empty())
{
if(q.size() == 1)
{
node* a = q.top();
q.pop();
r = a;
break;
}
else
{
node* a = q.top();
q.pop();
node* b = q.top();
q.pop();
node* c = new node();
c->weight = a->weight + b->weight;
c->lchild = a;
c->rchild = b;
r = c;
q.push(c);
}
}
return r;
}
void print() // 输出前缀编码
{
cout << WPL << endl;
for(int i=0; i<n; i++)
{
cout << str[i] << ":";
int index = str[i] - 'a';
for(int j=0; j<ans[index].size(); j++)
cout << ans[index][j];
cout << endl;
}
}
void dfs(node* root) // 深搜回溯得到哈夫曼编码和树的带权路径长度
{
if(root->lchild != NULL || root->rchild != NULL)
WPL += root->weight; // WPL即非叶子节点的权值之和
if(root->lchild == NULL && root->rchild == NULL)
{
char ch = root->ch;
ans[ch-'a'] = code; // 根据叶子节点的字符, 判断是谁的哈夫曼编码
return;
}
if(root->lchild != NULL)
{
code.push_back('0');
dfs(root->lchild);
code.pop_back(); // 回溯
}
if(root->rchild != NULL)
{
code.push_back('1');
dfs(root->rchild);
code.pop_back(); // 回溯
}
return;
}
int main()
{
cin >> n;
cin >> str;
for(int i=0; i<n; i++) // 读入各节点的权值, 利用优先队列维护小根堆, 便于建树
{
node* temp = new node(); // 不要忘记给指针分配空间
cin >> temp->weight;
temp->ch = str[i];
temp->lchild = temp->rchild = NULL;
q.push(temp);
}
node* root = createTree(); // 建立哈夫曼树
dfs(root); // 回溯得到哈夫曼编码及WPL
print();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号