PAT 1003 Emergency 统计最短路径
题目描述
原题链接
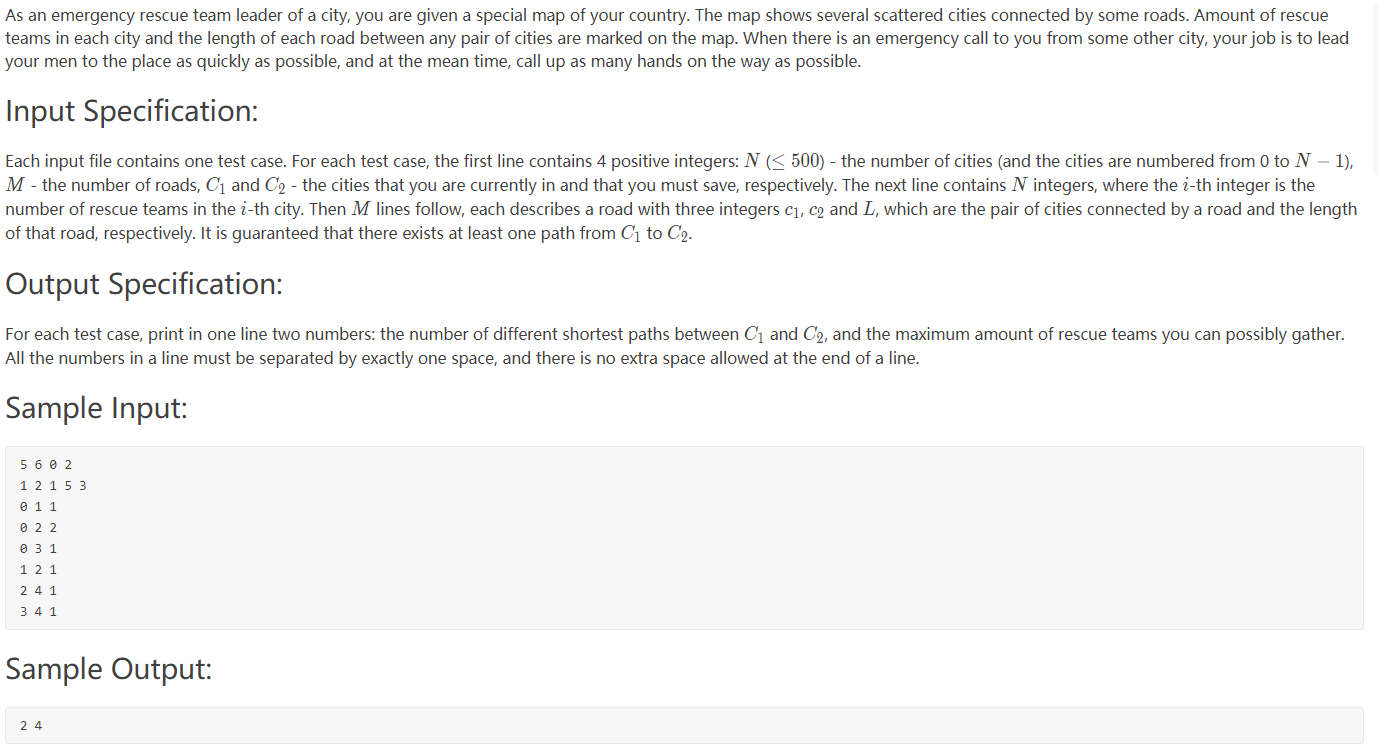
题目大概是要求出无向图中的最短路径条数, 还要求出所有最短路当中, 经过点的权值之和的最大值
实现1: DFS
分析:
题目数据量最大为500个点, 数据量较小, 可以进行dfs
代码:
// 500个点, 直接深搜
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 509;
const int INF = 0x3f3f3f3f;
int n, m, s, e;
int num[N]; // 各个点的权值
int map[N][N];
int vis[N];
int cnt, ans, min_dis; // 最短路径条数, 最短路径所经点的权值之和的最大值, 最短路径
void dfs(int pos, int dis, int count) // 当前所处顶点, 路径长度, 路径所经点的权值之和
{
if(pos == e)
{
if(dis < min_dis)
{
cnt = 1; // 如果这条路径的距离 < 当前的最短路径. 则重新计数
ans = count;
min_dis = dis;
}
else if(dis == min_dis)
{
cnt++; // 如果这条路径的距离 = 当前的最短路径. 则计数+1
ans = max(ans, count);
}
return;
}
for(int i=0; i<n; i++)
{
if(i!=pos && vis[i] == 0 && map[i][pos] != INF)
{
vis[i] = 1;
dfs(i,dis+map[i][pos],count+num[i]);
vis[i] = 0;
}
}
return;
}
int main()
{
cin >> n >> m >> s >> e;
for(int i=0; i<n; i++)
{
cin >> num[i];
}
memset(map,0x3f,sizeof(map));
for(int i=0; i<m; i++)
{
int a, b, c;
cin >> a >> b >> c;
map[a][b] = map[b][a] = min(map[a][b],c);
}
vis[s] = 1;
min_dis = INF;
dfs(s,0,num[s]);
cout << cnt << " " << ans << endl;
return 0;
}
实现2: 用Dijkstra求最短路的同时计数
如何求最短路的同时计数?
对于Dijkstra而言, 就是在松弛的同时进行计数
详见下段代码:
// ans[] 记录的是从各点到源点的最短路径条数
// cnt[] 是本题让求的多条最短路径中,经过点的权值之和的最大值
for(int j=0; j<n; j++)
{
if(!vis[j])
{
if(dist[j] > map[id][j] + mind)
//如果可以松弛, j到源点的最短路径数 = 中介点id到源点的最短路径数
{
dist[j] = map[id][j] + mind;
cnt[j] = cnt[id] + num[j];
ans[j] = ans[id];
}
else if(dist[j] == map[id][j] + mind)
// 如果j到源点的距离 = 从中介点id到j的最短距离 + 从id到源点的最短距离
// 那么j到源点的最短路径数 就要加上 中介点id到源点的最短路径数
{
ans[j] += ans[id];
cnt[j] = max(cnt[j], cnt[id] + num[j]);
}
}
}
完整代码
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 509;
const int INF = 0x3f3f3f3f;
int n, m, s, e;
int map[N][N];
int vis[N], dist[N], num[N], ans[N], cnt[N];
// 依次为 是否已访问 到源点的最短距离 该点的权值, 到源点的最短路径数 从n出发到源点的最短路径上经过的点的权值之和
void dijkstra()
{
// 初始化
for(int i=0; i<n; i++) dist[i] = INF;
dist[s] = 0;
ans[s] = 1; // 源点到源点的路径数为1
cnt[s] = num[s];
for(int i=0; i<n; i++)
{
int id = -1, mind = INF;
for(int j=0; j<n; j++)
{
if(!vis[j] && mind > dist[j])
{
mind = dist[j];
id = j;
}
}
vis[id] = 1;
for(int j=0; j<n; j++)
{
if(!vis[j])
{
if(dist[j] > map[id][j] + mind)
{
dist[j] = map[id][j] + mind;
cnt[j] = cnt[id] + num[j];
ans[j] = ans[id];
}
else if(dist[j] == map[id][j] + mind)
{
ans[j] += ans[id];
cnt[j] = max(cnt[j], cnt[id] + num[j]);
}
}
}
}
}
int main()
{
cin >> n >> m >> s >> e;
for(int i=0; i<n; i++)
{
cin >> num[i];
}
memset(map,0x3f,sizeof(map));
for(int i=0; i<m; i++)
{
int a, b, c;
cin >> a >> b >> c;
map[a][b] = map[b][a] = min(map[a][b],c);
}
dijkstra();
cout << ans[e] << " " << cnt[e] << endl;
return 0;
}
