AcWing 104. 货仓选址 贪心 绝对值不等式
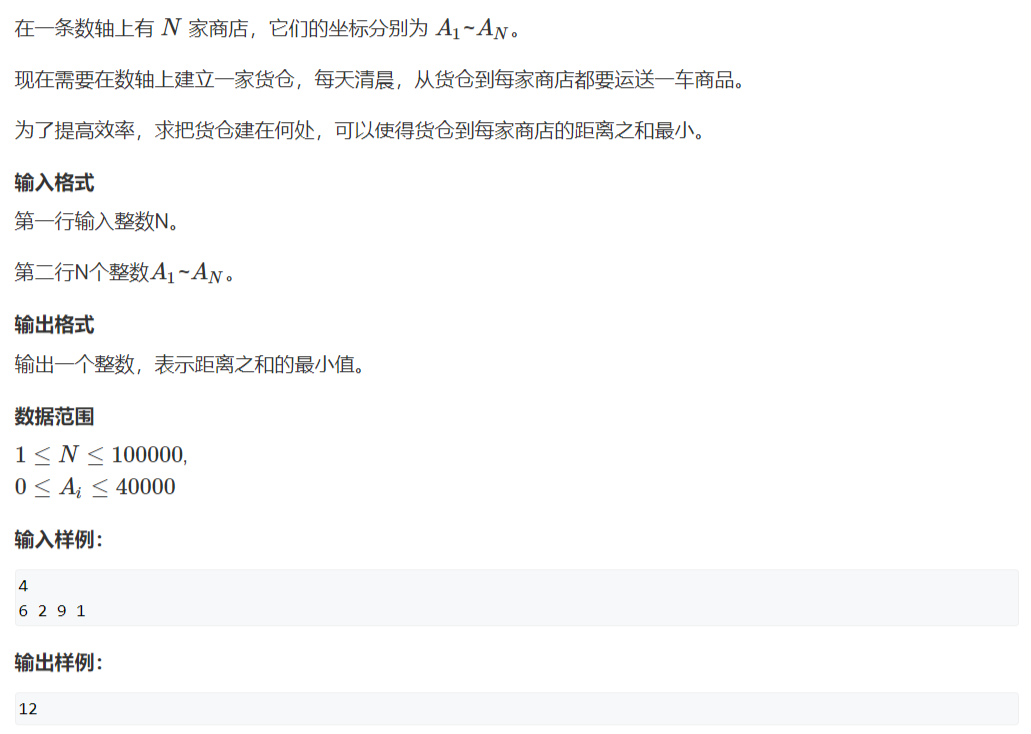
题目描述
分析
贪心
考虑只有两家商店 a , b a,b a,b. 货仓的位置 x x x到两家商店的距离 l l l就满足绝对值不等式` l = ∣ x − a ∣ + ∣ x − b ∣ ≥ ∣ a − b ∣ l = |x-a|+|x-b|≥|a-b| l=∣x−a∣+∣x−b∣≥∣a−b∣
则当 a ≤ x ≤ b a≤x≤b a≤x≤b时, 不等式取等,此时距离最小. 即货仓要建在两店之间(包括端点)
考虑 n n n家商店, n n n为奇数时, 建在最中间的商店处最优. n n n为偶数时, 建在最中间的两点之间
以上两种情况, 即中位数位置是最优解
实现
// 贪心, 利用绝对值不等式 |x-a| + |x-b| ≥ |a-b|(当a≤x≤b时取等)找到最小距离
// 考虑n个点, 奇数时, 建在最中间那个数的位置上, 偶数时,建在最中间两个数之间即可
// 综合两种情况, 可以认为建在中位数位置上距离最小
#include <cstdio>
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 1e5 + 9;
int n;
int a[N];
int sum;
int main()
{
cin >> n;
for(int i=0; i<n; i++)
{
cin >> a[i];
}
sort(a, a+n);
for(int i=0; i<n; i++)
{
sum += abs(a[n/2] - a[i]);
}
cout << sum << endl;
return 0;
}
nth_element
既然中位数就是最优解, 我们可以使用STL中的
nth_element来优化求出中位数的过程, 时间复杂度从 O ( n l o g n ) O(nlogn) O(nlogn)降至 O ( n ) O(n) O(n)
关于nth_element(firs,nth,last), 可以在 O ( n ) O(n) O(n)的复杂度下, 求出容器中第n大的数
nth_element的实现类似于快排一趟排序中元素相对于基准值的左移右移,可把nth看成基准值
nth_element并没有返回值, 要求的第n大的数的位置不变, 其他元素的位置发生改变(小的都在基准值前面, 大的都在后面)
代码
#include <cstdio>
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 1e5 + 9;
int n;
int a[N];
int sum;
int main()
{
cin >> n;
for(int i=0; i<n; i++)
{
cin >> a[i];
}
nth_element(a,a+n/2,a+n);
for(int i=0; i<n; i++)
{
sum += abs(a[n/2] - a[i]);
}
cout << sum << endl;
system("pause");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号