【NLP_Stanford课堂】文本分类1
文本分类实例：分辨垃圾邮件、文章作者识别、作者性别识别、电影评论情感识别（积极或消极）、文章主题识别及任何可分类的任务。
一、文本分类问题定义：
输入：
- 一个文本d
- 一个固定的类别集合C={c1,c2,...,cj}，一共j个类别
输出：一个d的预测类别c∈C
方法：
- 最简单的是使用基于词或其他特征组合的手写规则
- 垃圾邮件：列举出一系列黑名单的邮箱地址或者词（比如，“dollars”和“have been selected”）
- 如果规则很完备，准确率会非常高，但是一般很难做到或者花费会很贵
- 一般方法：结合手写规则和机器学习
二、有监督的机器学习方法：
输入：
- 一个文本d
- 一个固定的类别集合C={c1,c2,...,cj}，一共j个类别
- 一个训练集，其中包括m个已经被手动标记上类别的文档(d1,c1),...,(dm,cm)
输出：一个学习完毕的分类器γ: d→c，即给定一个新文档就可以输出一个对应的类别
分类器类别：
- Naive Bayes
- 逻辑回归
- 支持向量机Support-vector machines
- K近邻k-Nearest Neighbors
- ...
1. Naive Bayes
主要思想：非常简单，基于贝叶斯规则，用词袋表示文档
词袋：只统计文档中出现的单词本身及其计数，而忽略了词跟词之间的顺序，只是一个词的集合。词可以是文档中的词的全集或子集（即，只统计部分特征词），从而可以用一个词向量来表征文档
1.1 形式化描述：
对于一个文档d和一个类别c，我们旨在计算以下概率，，即给定一个文档，归属于该类别的概率是多少，从而找到最佳的类别：
最佳的匹配类别为：
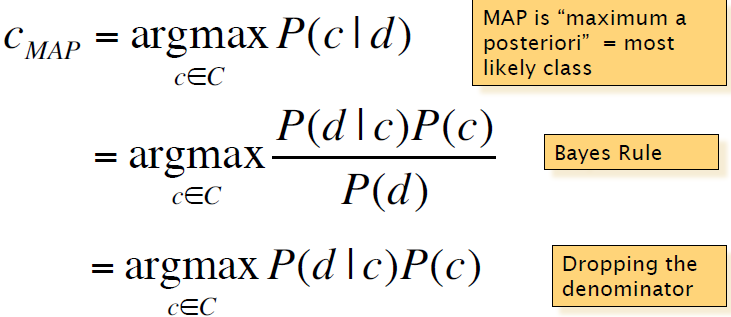
其中P(d|c)为最大似然概率，P(c)为先验概率
继而有：
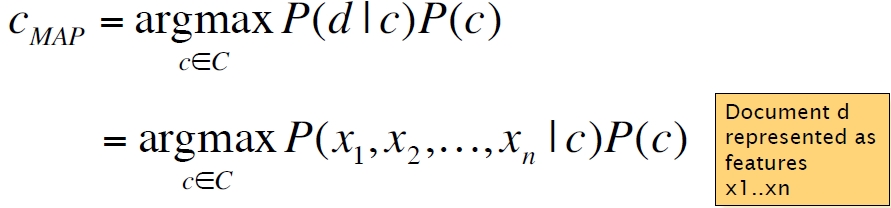
假定：
- Bag of Words assumption: 假定词的位置无关紧要，只关注是否出现某个词
- conditional independence条件独立性：假定给定类别c，各个特征x1,x2,...之间的概率P(xi|c)相互独立
当然以上的假设实际上并不正确，却能简化我们的计算问题，从而有：
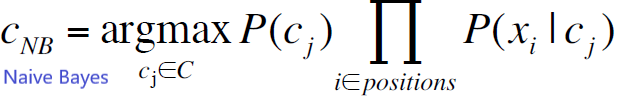
1.2 参数学习：
最简单的方法：使用最大似然估计
这里需要将属于类别cj的文档都连接在一起，创建一个新的大文档，然后计算wi在该大文档中的频次
然而实际上，我们并不在naive Bayes中使用最大似然估计，因为：
- 当测试集中出现训练集中没有的词时，会按照训练集中的计数被记为0，而当一个测试文档中出现一个类别cj中未知的词时，该文档属于cj的概率会是0，因为是连乘。
解决方法：增加一个平滑
Add-1：
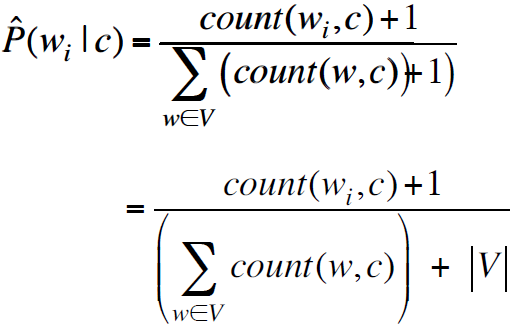
1.2.1 具体步骤：
- 从训练集中提取词汇表V
- 计算每一个类别的P(cj)
- 将所有属于cj类别的文档放入一个集合docsj
- 计算：
- 计算类别cj下文档中的某个词wk的条件概率P(wk|cj)
- 将docsj中的文档连接成一个文档Textj
- 对于词汇表中的每个词，计算：
- wk在Textj中出现的次数nk
，其中α是增加的一个平滑
1.2.2 如何应对未知词：
在词汇表中增加一个词“unknown word”，用wu表示。
由于在训练集中不存在未知词，所以count(wu,c)=0，条件概率为：
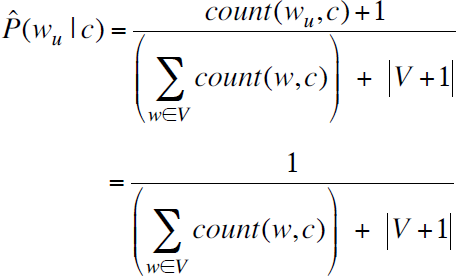
2. Naive Bayes与语言模型的关系
根据一个类别，我们可以围绕这个类别生成一个文本，其跟语言模型非常相似
假设：每个类别=一个unigram语言模型
证明：
在Naive Bayes中，对于文档中的一个词有一个归属于一个类别的概率：P(word | c)。从而每个句子有：
。例子如下：
文档为：“I love this fun film”。类别为：postive。则每个词归属于positive的概率为左列所示。
则整个句子的概率为：
而unigram语言模型在计算概率时为P(s)=ΠP(word)
所以Naive Bayes其实就是一个已知类别下的unigram语言模型。
当我们在检验不同类别下句子的概率时，就好比在运行不同的语言模型，比如postive和negtive
所以寻找概率最高的归属类别的过程就变成了寻找概率最高的语言模型的过程。
3. 多项式Naive Bayes模型的实例
3.1新闻分类
设我们要对亚洲新闻进行分类，训练集中有四个文档，每个文档归属于chinese或japanese，测试集中有一个文档，要求对这个文档进行分类。P(c)和P(w | c)的计算方法如上所示。
解：
1) 首先计算P(c)：
2) 然后计算P(w | c)：统计词汇表中一共有6个单词：Chinese, Beijing, Shanghai, Macao, Tokyo, Japan。由于测试集中只有3个单词：Chinese，Tokyo，Japan，所以方便起见我们只计算这三个词的条件概率如下：
以P(Chinese|c)为例，Chinese在c这个类别下出现了5次，c这个类别下一共有3+3+2=8个词，词汇表一共有6个词，则根据公式可以计算得到结果为6/14=3/7
3) 然后计算P(c|d5)：d5表示第5篇文档，即测试文档，表示已知文档d5，求归属类别。
因为P(c|d5)=P(d5|c)*P(c)/P(d5)=ΠP(word|c)*P(c)/P(d5)v9 ∝ ΠP(word|c)*P(c)，所以：
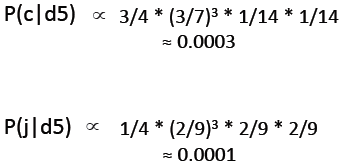
P(c|d5)>P(j|d5)，所以测试文档的类别应为c
3.2 垃圾邮件过滤
上述新闻分类的实例中采用每个词作为特征，但是大部分应用中选用的是特殊种类的词和其他作为特征。在垃圾邮件检测中，采用以下作为特征：
