noip2015
D1T3:
题目描述
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏
。在斗地主中,牌的大小关 系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<{小王}<{大王}
而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由 n 张牌组成。游戏者每次可以根据规定的牌型进行出牌
,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。具体规则如下:
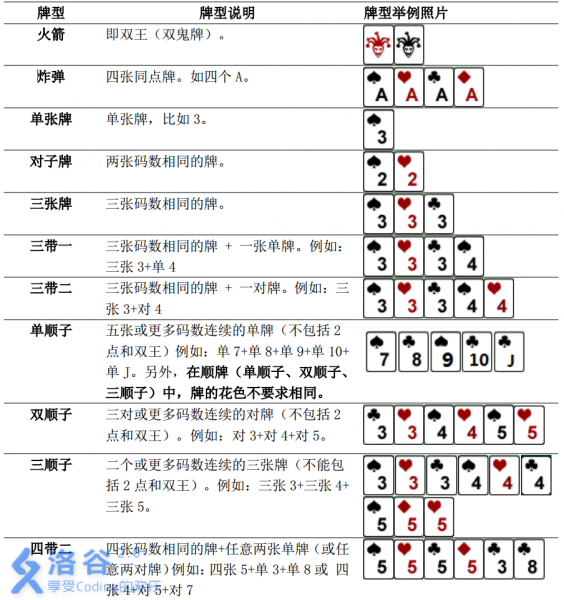
输入输出格式
输入格式:
第一行包含用空格隔开的2个正整数 T,n ,表示手牌的组数以及每组手牌的张数。
接下来 T 组数据,每组数据 n行,每行一个非负整数对 ai,bi ,表示一张牌,其中ai 表示牌的数码,
bi 表示牌的花色,中间用空格隔开。特别的,我们用 1 来表示数码 A, 11表示数码J, 12 表示数码Q, 13表示数码 K;
黑桃、红心、梅花、方片分别用 1-4 来表示;小王的表示方法为 01 ,大王的表示方法为 02 。
输出格式:
共 T 行,每行一个整数,表示打光第 ii 组手牌的最少次数。
输入输出样例
1 8 7 4 8 4 9 1 10 4 11 1 5 1 1 4 1 1
3
总之是道无聊的搜索题,我们先分析题目,可以发现,本题和大小无关,花色无关,
而且在没有顺子的情况下,直接贪心就可以求得最后解,所以我们对顺子的情况进行搜索
只需要搜出那些顺子就可以了
(ps:考研你的编程能力!!!相信自己!!!每次写一个函数就要证明它的正确性!!!ac之后不要乱改动)
I'm being mad!
:
#include<cstdio> #include<algorithm> #include<iostream> #include<cstring> #include<cstdlib> #include<cmath> using namespace std; const int maxn=15; template<typename T> inline void read(T &a){ a=0;T b=1;char x=getchar(); while(x<'0'||'9'<x){ if(x=='-')b=-1; x=getchar(); } while('0'<=x&&x<='9'){ a=(a<<1)+(a<<3)+x-'0'; x=getchar(); } a*=b; } char ch[50]; int temp; template<typename T > inline void print(T a){ if(a<0){ putchar('-'); a=-a; } do{ ch[++temp]=a%10+'0'; a/=10; }while(a); while(temp)putchar(ch[temp--]); putchar('\n'); } int n,ans,t,sum[maxn]; int cnt[5]; inline int CNT(){return cnt[1]+cnt[2]+cnt[3]+cnt[4];} inline int get_step(){ memset(cnt,0,sizeof(cnt)); for(int i=0;i<=14;i++){ //双王参与带牌 cnt[ sum[i] ]++; } for(int i=cnt[4];i;i--){ //4 and 2 if(cnt[1]>=2)cnt[1]-=2; else if(cnt[2]>=2)cnt[2]-=2; } for(int i=cnt[3];i;i--){ if(cnt[1])cnt[1]--; else if(cnt[2])cnt[2]--; } return CNT(); } inline void shunzi(int k,int l,int r){ for(int i=l;i<=r;i++)sum[i]-=k; } void dfs(int step){ //顺子个数, ans=min(ans,step+get_step()); int conti_one,conti_two,conti_three; conti_one=conti_two=conti_three=0; for(int i=3;i<=14;i++){ //3~A if(sum[i]){ if(sum[i-1]&&i>=4)conti_one++; else conti_one=1; } else conti_one=0;//我怎么会犯如此傻逼的问题??? if(sum[i]>=2){ if(sum[i-1]>=2&&i>=4)conti_two++; else conti_two=1; } else conti_two=0;//我怎么会犯如此傻逼的问题??? if(sum[i]>=3){ if(sum[i-1]>=3&&i>=4)conti_three++; else conti_three=1; } else conti_three=0;//我怎么会犯如此傻逼的问题??? if(conti_one>=5){ for(int j=i-conti_one+1;j<=i-4;j++){ //枚举顺子区间 shunzi(1,j,i); dfs(step+1); shunzi(-1,j,i); } } if(conti_two>=3){ for(int j=i-conti_two+1;j<=i-2;j++){ //枚举顺子区间 shunzi(2,j,i); dfs(step+1); shunzi(-2,j,i); } } if(conti_three>=3){ for(int j=i-conti_three+1;j<=i-2;j++){ //枚举顺子区间 shunzi(3,j,i); dfs(step+1); shunzi(-3,j,i); } } } } int main() //如果没有 顺子,那么可以直接 贪心,所以枚举顺子 { scanf("%d%d",&t,&n); while(t--){ memset(sum,0,sizeof(sum)); int bb,a; ans=n; for(int i=1;i<=n;i++){ scanf("%d%d",&a,&bb); if(a==1)a=14; sum[a]++; } dfs(0); printf("%d\n",ans); } return 0; }
D1T2:
个人感觉傻逼题,虽然因为文件问题没有分
多种方法
第一种:正宗的tarjan
证明:
每个点只指向一个点,所以每个联通分量都是环,所以直接tarjan然后记录环里点的个数==路径长
第二种:并查集???
我也不知道怎么写的,貌似并查集的时候就能找到环?但是acl了,并不建议
第三种:topological sort
仔细想下发现是对的,我们会拓扑找最长链,所以类比一下把所有indegree==0的点删除,最后剩的一定是环,直接dfs求长度
D2T1:
60`贪心:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #include<cstdlib> #include<cmath> #include<queue> using namespace std; const int maxn=5e4+5; const int INF=1e9; inline int read(){ int a=0;bool b=1;char x=getchar(); while(x<'0'&&'9'<x){ if(x=='-')b=0; x=getchar(); } while('0'<=x&&x<='9'){ a=(a<<1)+(a<<3)+x-'0'; x=getchar(); } return b ? a : -a ; } priority_queue<pair<int ,int > >q; int l,m,n,dis[maxn],a[maxn]; int pre[maxn],suf[maxn]; bool vis[maxn];//鏍囪杩欐鏄惁 瀛樺湪 inline void add(int i){ pre[i]=i-1;suf[i]=i+1; q.push(make_pair(-dis[i],i));//淇濊瘉灏忔牴鍫? } inline void del(int pos){ int l=pre[pos];int r=suf[pos]; suf[l]=r;pre[r]=l; vis[pos]=1; m--; } int main() { freopen("stone.in","r",stdin); freopen("stone.out","w",stdout); l=read();n=read();m=read(); for(int i=1;i<=n;i++){ a[i]=read(); dis[i]=a[i]-a[i-1];//璁板綍姣忔鐨勮窛绂? //閾捐〃鏋勫缓 add(i); } dis[n+1]=l-a[n];//鏈€鍚庝竴姝?鍏眓+1姝? add(n+1); dis[0]=dis[n+2]=INF; if(m==n){ printf("%d",l); return 0; } while(m){ int pos=q.top().second; q.pop(); if(vis[pos])continue; int left=pre[pos];int right=suf[pos]; if(dis[left]+dis[pos]>dis[right]+dis[pos]){ del(right); dis[pos]+=dis[right]; q.push(make_pair(-dis[pos],pos)); } else{ del(left); dis[pos]+=dis[left]; q.push(make_pair(-dis[pos],pos)); } } while(vis[ q.top().second])q.pop(); printf("%d",-q.top().first); return 0; }
D2T1:
贪心反例:3 1 1 3
60·:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #include<cstdlib> #include<cmath> #include<queue> using namespace std; const int maxn=5e4+5; const int INF=1e9; inline int read(){ int a=0;bool b=1;char x=getchar(); while(x<'0'&&'9'<x){ if(x=='-')b=0; x=getchar(); } while('0'<=x&&x<='9'){ a=(a<<1)+(a<<3)+x-'0'; x=getchar(); } return b ? a : -a ; } priority_queue<pair<int ,int > >q; int l,m,n,dis[maxn],a[maxn]; int pre[maxn],suf[maxn]; bool vis[maxn];//鏍囪杩欐鏄惁 瀛樺湪 inline void add(int i){ pre[i]=i-1;suf[i]=i+1; q.push(make_pair(-dis[i],i));//淇濊瘉灏忔牴鍫? } inline void del(int pos){ int l=pre[pos];int r=suf[pos]; suf[l]=r;pre[r]=l; vis[pos]=1; m--; } int main() { freopen("stone.in","r",stdin); freopen("stone.out","w",stdout); l=read();n=read();m=read(); for(int i=1;i<=n;i++){ a[i]=read(); dis[i]=a[i]-a[i-1];//璁板綍姣忔鐨勮窛绂? //閾捐〃鏋勫缓 add(i); } dis[n+1]=l-a[n];//鏈€鍚庝竴姝?鍏眓+1姝? add(n+1); dis[0]=dis[n+2]=INF; if(m==n){ printf("%d",l); return 0; } while(m){ int pos=q.top().second; q.pop(); if(vis[pos])continue; int left=pre[pos];int right=suf[pos]; if(dis[left]+dis[pos]>dis[right]+dis[pos]){ del(right); dis[pos]+=dis[right]; q.push(make_pair(-dis[pos],pos)); } else{ del(left); dis[pos]+=dis[left]; q.push(make_pair(-dis[pos],pos)); } } while(vis[ q.top().second])q.pop(); printf("%d",-q.top().first); return 0; }
二分答案:
ac:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #include<cstdlib> #include<cmath> #include<queue> using namespace std; const int maxn=5e4+5; const int INF=1e9; inline int read(){ int a=0;bool b=1;char x=getchar(); while(x<'0'&&'9'<x){ if(x=='-')b=0; x=getchar(); } while('0'<=x&&x<='9'){ a=(a<<1)+(a<<3)+x-'0'; x=getchar(); } return b ? a : -a ; } int l,n,m,a[maxn],dis[maxn]; inline bool judge(int ans){//二分答案部分 int cnt=0,temp=0; for(int i=1;i<=n+1;i++){ cnt+=dis[i]; if(cnt>=ans)cnt=0,temp++; } return (n-temp+1)<=m; } int main() { //freopen("a.in","r",stdin); //freopen("stone2.out","w",stdout); l=read();n=read();m=read(); for(int i=1;i<=n;i++){ a[i]=read(); dis[i]=a[i]-a[i-1]; } dis[n+1]=l-a[n]; int left=1;int right=l; while(left+1<right){ int mid=(left+right)>>1; if(judge(mid)){ left=mid; } else{ right=mid; } mid=(left+right)>>1; } if(judge(right))printf("%d",right); else printf("%d",left); return 0; }
D2T2:
force:空间不够,内存不够
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; inline int read(){ int a=0;bool b=1;char x=getchar(); while(x<'0'&&'9'<x){ if(x=='-')b=0; x=getchar(); } while('0'<=x&&x<='9'){ a=(a<<1)+(a<<3)+x-'0'; x=getchar(); } return b ? a : -a ; } const int maxn=1e3+5; const int maxm=2e2+5; const int P=1000000007; int f[maxn][maxm][maxm/2];//maxm/=2 因为会爆空间
//f[i][j][k]琛ㄧずA涓插尮閰嶅埌i浣嶇疆涓烘锛孊涓插尮閰嶅埌j浣嶇疆涓烘锛屽彇鍑簁涓?瀛愪覆 鎵€鐢ㄧ殑鏂规鏁? //f[i][j][k]=sum(f[0~i][j-len [i] ] [k-1]) int n,m,k; char a[maxn],b[maxm]; int main() { freopen("substring.in","r",stdin); freopen("substring.out","w",stdout); n=read();m=read();k=read(); scanf("%s",a+1); scanf("%s",b+1); f[0][0][0]=1; for(int kk=1;kk<=k;kk++){ for(int j=kk;j<=m;j++){ for(int i=j;i<=n;i++){ int cnt=0; while(a[i-cnt]==b[j-cnt]&&j!=cnt){ for(int ii=i-cnt-1;ii>=j-cnt-1;ii--){ f[i][j][kk]=(f[i][j][kk]+f[ii][j-cnt-1][kk-1])%P; //涓嶅ソ缁存姢銆傘€傘€? //printf("%d",kk-1); //printf("%d %d %d %d\n",i,j,kk,f[i][j][kk]); } cnt++; } } } } int ans=0; for(int i=k;i<=n;i++){ ans=(ans+f[i][m][k])%P; } printf("%d",ans); return 0; }
DP优化:循序渐进思考法
!!!常用技巧:通过增加1维度状态,来减少转移方程的复杂度,0->不匹配,1->匹配!!!
原理:通过把状态进行总结,分成对转移有影响的两类状态,从而降低之间复杂度
70':
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; inline int read(){ int a=0;bool b=1;char x=getchar(); while(x<'0'&&'9'<x){ if(x=='-')b=0; x=getchar(); } while('0'<=x&&x<='9'){ a=(a<<1)+(a<<3)+x-'0'; x=getchar(); } return b ? a : -a ; } const int maxn=1e3+5; const int maxm=2e2+5; const int P=1000000007; int f[maxn][maxm][maxm/2];//f[i][j][k]琛ㄧずA涓插尮閰嶅埌i浣嶇疆涓烘锛孊涓插尮閰嶅埌j浣嶇疆涓烘锛屽彇鍑簁涓?瀛愪覆 鎵€鐢ㄧ殑鏂规鏁? //f[i][j][k]=sum(f[0~i][j-len [i] ] [k-1]) int n,m,k; char a[maxn],b[maxm]; int main() { //freopen("substring.in","r",stdin); //freopen("substring.out","w",stdout); n=read();m=read();k=read(); scanf("%s",a+1); scanf("%s",b+1); for(int i=0;i<=n;i++){ f[i][0][0]=1; } for(int kk=1;kk<=k;kk++){ for(int j=kk;j<=m;j++){ for(int i=j;i<=n;i++){ f[i][j][kk]=f[i-1][j][kk]; //状态转移决策:a[i]参与成串or a[i]不参与成串 int cnt=0; while(a[i-cnt]==b[j-cnt] && i!=cnt && j!=cnt){ f[i][j][kk]=(f[i][j][kk]+f[i-cnt-1][j-cnt-1][kk-1])%P; cnt++; } //if(j==3&&i==6)printf("%d",f[6][3][1]); } } } printf("%d",f[n][m][k]); return 0; }
force2:空间爆了时间够
#include<cstdio> #include<algorithm> #include<iostream> #include<cstring> #include<cstdlib> #include<cmath> #define LL long long using namespace std; template<typename T> inline void read(T &a){ a=0;T b=1;char x=getchar(); while(x<'0'||'9'<x){ if(x=='-')b=-1; x=getchar(); } while('0'<=x&&x<='9'){ a=(a<<1)+(a<<3)+x-'0'; x=getchar(); } a*=b; } char ch[50]; int temp; template<typename T> inline void print(T a){ if(a<0){ putchar('-'); a=-a; } do{ ch[++temp]=a%10+'0'; a/=10; }while(a); while(temp)putchar(ch[temp--]); } const int maxn=1e3+5; const int maxm=2e2+5; const LL P=1000000007; int n,m,k; char a[maxn],b[maxm]; LL f[maxn][maxm/2][maxm/2][2]; /*f[i][j][k][b]表示A串匹配到i位置,B串匹配到j位置 分成k个子串的方案数,b=1:i位置选上 b=0:i位置没选 */ int main() { read(n);read(m);read(k); scanf("%s%s",a+1,b+1); for(int i=0;i<=n;i++)f[i][0][0][0]=1; for(int kk=1;kk<=k;kk++){ for(int j=kk;j<=m;j++){ for(int i=j;i<=n;i++){ f[i][j][kk][0]=(f[i-1][j][kk][0]+f[i-1][j][kk][1])%P; if(a[i]==b[j]) f[i][j][kk][1]=(f[i-1][j-1][kk][1]+f[i-1][j-1][kk-1][0]+f[i-1][j-1][kk-1][1])%P; } } } print((f[n][m][k][0]+f[n][m][k][1])%P); return 0; }
std:
如何优化空间?滚动数组啊,当初学背包的时候就讲了滚动数组可以 优化空间or无限背包
ac:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cmath>
#define LL long long
using namespace std;
template<typename T>
inline void read(T &a){
a=0;T b=1;char x=getchar();
while(x<'0'||'9'<x){
if(x=='-')b=-1;
x=getchar();
}
while('0'<=x&&x<='9'){
a=(a<<1)+(a<<3)+x-'0';
x=getchar();
}
a*=b;
}
char ch[50];
int temp;
template<typename T>
inline void print(T a){
if(a<0){
putchar('-');
a=-a;
}
do{
ch[++temp]=a%10+'0';
a/=10;
}while(a);
while(temp)putchar(ch[temp--]);
}
const int maxn=1e3+5;
const int maxm=2e2+5;
const LL P=1000000007;
int n,m,k,now;
char a[maxn],b[maxm];
LL f[maxn][maxm][2][2];
/*f[i][j][k][b]表示A串匹配到i位置,B串匹配到j位置
分成k个子串的方案数,b=1:i位置选上 b=0:i位置没选 */
//滚动数组写法:
int main()
{
read(n);read(m);read(k);
scanf("%s%s",a+1,b+1);
for(int i=0;i<=n;i++)f[i][0][0][0]=1;
now=1;
for(int kk=1;kk<=k;kk++){
for(int j=kk;j<=m;j++){
for(int i=j;i<=n;i++){
f[i][j][now][0]=(f[i-1][j][now][0]+f[i-1][j][now][1])%P;
if(a[i]==b[j])
f[i][j][now][1]=(f[i-1][j-1][now][1]+f[i-1][j-1][now^1][0]+f[i-1][j-1][now^1][1])%P;
else f[i][j][now][1]=0;
}
}
now^=1;
for(int j=1;j<=m;j++)
for(int i=1;i<=n;i++){
f[i][j][now][0]=f[i][j][now][1]=0;
}
}
print((f[n][m][now^1][0]+f[n][m][now^1][1])%P);
return 0;
}
D2T3:
force:m=1(20')
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #include<cstdlib> #define LL long long using namespace std; inline int read(){ int a=0;bool b=1;char x=getchar(); while(x<'0'&&'9'<x){ if(x=='-')b=0; x=getchar(); } while('0'<=x&&x<='9'){ a=(a<<1)+(a<<3)+x-'0'; x=getchar(); } return b ? a : -a ; } const int maxn=300000; int first[maxn],next[maxn*2],to[maxn*2],w[maxn*2],edge_count; inline void add(int x,int y,int q){ edge_count++; to[edge_count]=y; w[edge_count]=q; next[edge_count]=first[x]; first[x]=edge_count; } int n,m; int f[maxn][30],maxedge[maxn][30],log[maxn],deep[maxn]; LL dis_root[maxn]; inline void build(int u,int fa){ deep[u]=deep[fa]+1; for(int i=1;i<=log[ deep[u] ];i++){ f[u][i]=f[ f[u][i-1] ][i-1]; maxedge[u][i]=max(maxedge[u][i-1],maxedge[f[u][i-1]][i-1]); } for(int i=first[u];i;i=next[i]){ int v=to[i]; if(v==fa)continue; f[v][0]=u; maxedge[v][0]=w[i]; dis_root[v]=dis_root[u]+(LL)w[i]; build(v,u); } } inline void LCA_init(){ deep[1]=1; dis_root[1]=0ll; for(int i=2;i<=n;i++){ log[i]=log[i>>1]+1; } build(1,0); } inline int lca(int x,int y){ if(deep[x]<deep[y])swap(x,y); for(int i=log[deep[x]];i>=0;i--){ if(deep[y]<=deep[f[x][i]]){ x=f[x][i]; } } if(x==y)return x; for(int i=log[deep[x]];i>=0;i--){ if(f[x][i]!=f[y][i]){ x=f[x][i];y=f[y][i]; } } return f[x][0]; } inline int LCA(int x,int y){ int ans=0; if(deep[x]!=deep[y]) { if(deep[x]<deep[y])swap(x,y); for(int i=log[deep[x]];i>=0;i--){ if(deep[y]<deep[f[x][i]]){ x=f[x][i]; ans=max(ans,maxedge[x][i]); } } if(f[x][0]==y)return ans; if(deep[x]==deep[y]+1)x=f[x][0]; } for(int i=log[deep[x]];i>=0;i--){ if(f[x][i]!=f[y][i]){ x=f[x][i];y=f[y][i]; ans=max(ans,max(maxedge[x][i],maxedge[y][i])); } } return max(ans,max(maxedge[x][0],maxedge[y][0])); } inline void force(){ LCA_init(); int a=read();int b=read(); printf("%lld",dis_root[a]+dis_root[b]-2*dis_root[lca(a,b)]-(LL)LCA(a,b)); } int main() { freopen("transport.in","r",stdin); freopen("transport.out","w",stdout); n=read();m=read(); for(int i=1,a,b,t;i<n;i++){ a=read();b=read();t=read(); add(a,b,t);add(b,a,t); } if(m==1)force(); else { LCA_init(); LL Max; for(int i=1,a,b;i<=m;i++){ a=read();b=read(); LL t=dis_root[a]+dis_root[b]-2*dis_root[lca(a,b)]-(LL)LCA(a,b); if(t>Max)Max=t; } printf("%lld",Max); } return 0; }
std:
#include<cstdio> #include<cstring> #include<algorithm> #include<cstdlib> #define LL long long using namespace std; template<typename T> inline void read(T &a){ a=0;T b=1;char x=getchar(); while(x<'0'||'9'<x){ if(x=='-')b=-1; x=getchar(); } while('0'<=x&&x<='9'){ a=(a<<1)+(a<<3)+x-'0'; x=getchar(); } a*=b; } char C[50]; int temp; template<typename T > inline void write(T a){ if(a<0){ a=-a; putchar('-'); } do{ C[++temp]=a%10+'0'; a/=10; }while(a); while(temp)putchar(C[temp--]); } /*main thought: 最大值最小,二分答案 计算每个答案,对于距离<=ans的路径,直接跳过, 对于距离>ans的路径 ,树上差分,选择公共边里最大的 并验证 */ int n,m; const int maxn=3e5+5; int first[maxn],next[maxn*2],to[maxn*2],edge_count; LL w[maxn*2]; inline void add(int x,int y,LL l){ edge_count++; to[edge_count]=y; w[edge_count]=l; next[edge_count]=first[x]; first[x]=edge_count; } int deep[maxn],log[maxn],f[maxn][30]; LL dis_root[maxn]; void build(int u,int fa){ deep[u]=deep[fa]+1; for(int i=1;i<=log[deep[u]];i++){ f[u][i]=f[f[u][i-1]][i-1]; } for(int i=first[u];i;i=next[i]){ int v=to[i]; if(v==fa)continue; f[v][0]=u; dis_root[v]=dis_root[u]+w[i]; build(v,u); } } inline void LCA_init(){ deep[1]=1; for(int i=2;i<=n;i++)log[i]=log[i>>1]+1; build(1,0); } inline int LCA(int x,int y){ if(deep[x]<deep[y])swap(x,y); for(int i=log[deep[x]];i>=0;i--){ if(deep[y]<=deep[f[x][i]])x=f[x][i]; } if(x==y)return x; for(int i=log[deep[x]];i>=0;i--){ if(f[x][i]!=f[y][i]){ x=f[x][i];y=f[y][i]; } } return f[x][0]; } struct Edge{ int u,v,lca; LL dis; inline void update(){ lca=LCA(u,v); dis=dis_root[u]+dis_root[v]-2*dis_root[lca]; } }e[maxn]; int cnt,cover[maxn]; LL max_dis,max_edge; void dfs(int u,int fa){ for(int i=first[u];i;i=next[i]){ int v=to[i]; if(v==fa)continue; dfs(v,u); if(cover[v]==cnt)max_edge=max(max_edge,w[i]); cover[u]+=cover[v]; } } inline bool judge(LL dis){ cnt=0;memset(cover,0,sizeof(cover)); max_edge=max_dis=0; for(int i=1;i<n;i++){ if(e[i].dis>dis){ cover[e[i].u]++; cover[e[i].v]++; cover[e[i].lca]-=2; max_dis=max(max_dis,e[i].dis); cnt++; } } dfs(1,0); return max_dis-max_edge<=dis; } LL left,right,mid; int main() { //freopen("transport.in","r",stdin); //freopen("transport.out","w",stdout); read(n);read(m); for(int i=1;i<n;i++){ int a,b;LL t; read(a);read(b);read(t); add(a,b,t);add(b,a,t); } LCA_init(); //printf("%d ",LCA(4,5)); for(int i=1;i<=m;i++){ read(e[i].u);read(e[i].v); e[i].update(); right=max(right,e[i].dis); //printf("%d %lld\n",e[i].lca,e[i].dis); } mid=(left+right)>>1; while(left+1<right){ if(judge(mid))right=mid; else left=mid; mid=(left+right)>>1; } if(judge(left))write(left); else write(right); return 0; }


