用树状数组处理逆序对[数据结构][树状数组]
逆序对
——!x^n+y^n=z^n
可以到这里[luogu]:
https://www.luogu.org/problem/show?pid=1908
题意:对于给定的一段正整数序列,逆序对就是序列中ai>aj且i<j的有序对。知道这概念后,他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。
假如为这些数为:
8 2 3 1 7
如果我们把数一个个加进来,用一个数组a[i]统计i出现了几次。
a的初始状态:
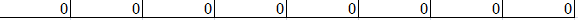
8加进来后:
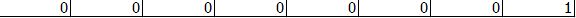
由于不存在比8大的数,说明没有产生逆序对
2加进来后:
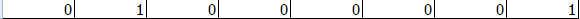
统计比2大的数(即产生逆序对),有一个
3加进来后:

逆序对+1
...
可能大家都看出来了,即每次加入统计前面的数有几个比自己大,即统计后面的数有几个,这种事情当然用树状数组操作很方便。
其实如果大家在想一想,如果我把这些数倒过来看,那我们就是要统计前面有几个数比自己小,这不就和树状数组操作一模一样?
当然在进行上述操作可能就看出问题了,就是4,5,6这些是没用的,这样不仅费时还费空间。
其实上面的数和
5 2 3 1 4 的逆序对数是一样的,这样我们的操作就完美了。(当然你要主要有几个数是一样的情况)
附上Lowbee的代码
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 using namespace std; 6 #define maxn 100010 7 struct lys{ 8 int pos,v; 9 }p[maxn]; 10 int bit[maxn],a[maxn]; 11 inline int read(); 12 namespace Liisa{ 13 int n; 14 int lowbit(int x){ 15 return x&(-x); 16 } 17 bool cmp(const lys &a,const lys &b){ 18 return a.v<b.v; 19 } 20 //插入,或者理解为单点更新 21 void insert(int x){ 22 int i; 23 for(i=x;i<=n;i+=lowbit(i)) 24 bit[i]++; 25 } 26 //统计和 27 long long getsum(int x){ 28 int i; 29 long long res=0; 30 for(i=x;i>0;i-=lowbit(i)) 31 res+=bit[i]; 32 return res; 33 } 34 long long ans=0; 35 int main(){ 36 n=read(); 37 int i; 38 for(i=1;i<=n;i++){ 39 p[i].pos=i; p[i].v=read(); 40 } 41 sort(p+1,p+1+n,cmp); 42 int s=0; 43 p[0].v=-1; 44 //离散化操作 45 for(i=1;i<=n;i++){ 46 if(p[i].v!=p[i-1].v) s++; 47 a[p[i].pos]=s; 48 } 49 //计算逆序对,从后往前读 50 for(i=n;i>=1;i--){ 51 insert(a[i]); 52 //统计比自己小的 53 ans+=getsum(a[i]-1); 54 } 55 cout<<ans<<endl; 56 } 57 } 58 int main(){ 59 Liisa::main(); 60 return 0; 61 } 62 inline int read(){ 63 int k=0,f=1; 64 char c=getchar(); 65 while(c>'9'||c<'0'){ 66 if(c=='-') f=-1; 67 c=getchar(); 68 } 69 while(c>='0'&&c<='9'){ 70 k=k*10+c-'0'; 71 c=getchar(); 72 } 73 return k*f; 74 }
如有错误,欢迎指正。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号