[数学]对数均值不等式

I think, therefore I am.

——Descartes

---

对数均值不等式

\[\sqrt{x_1x_2}\leq\frac{x_1-x_2}{\ln{x_1}-\ln{x_2}}\leq\frac{x_1+x_2}{2}\ ({x_1},{x_2}\in\R^+\ and\ {x_1}\neq{x_2}) \]

1. Proof Method(证明方法)

对于 \((\ln{x_1}-\ln{x_2})\) 式子常做齐次化处理，换元构造一元新函数在进行研究一般可以得到比较好的效果。

我们以左边的不等号证明作为例子：

\[不妨设\ 0<x_1<x_2\\ \sqrt{x_1x_2}\leq\frac{x_1-x_2}{\ln{x_1}-\ln{x_2}}\\ \Leftrightarrow\ln{\frac{x_2}{x_1}\leq\sqrt{\frac{x_2}{x_1}}-\sqrt{\frac{x_1}{x_2}}}\\ 于是我们令\ t\ =\sqrt\frac{x_2}{x_1}>1，则有：\\ 不等式\Leftrightarrow2\ln{t}-t+\frac{1}{t}\leq0\ (t>1)\\ 令f(x)=2\ln x-x+\frac 1{x}，f^{'}(x)=\frac 2 x-1-\frac 1 {x^2}=-{(\frac 1 x-1)^2}\leq0\\ \therefore\ f(x)在(1,+\infty)单调递减\Rightarrow\ f(x)<f(1)=0\Rightarrow\ 原不等式成立 \]

2. Geometric Meaning(几何意义)

在 $y=\ln x$ 任取两点 $A，B$ ，如上图所示。以右边 $\frac{x_1-x_2}{\ln{x_1}-\ln{x_2}}\leq\frac{x_1+x_2}{2}$ 为例进行说明： $$ \Leftrightarrow\frac 2 {x_1+x_2}\leq\frac{\ln{x_1}-\ln{x_2}}{x_1-x_2} $$ 为方便起见，记 $A，B$ 在 $y=\ln x$ 的中点为 $D$ ，并过 $D$ 做函数 $y=\ln x$ 的切线 $l$ ，则 $\frac{\ln{x_1}-\ln{x_2}}{x_1-x_2}$ 即为 $AB$ 直线的斜率 $k_1$ ，而 $\frac{2}{x_1+x_2}$ 即为 $l$ 的斜率 $k_2$ 。那么，由上面的结论立马可以得到： $$ \frac 2 {x_1+x_2}\leq\frac{\ln{x_1}-\ln{x_2}}{x_1-x_2}\Rightarrow k_1\geq k_2 $$ 这个不等式实际上告诉我们：在 $y=\ln x$ 的图像上任意两点的斜率大于其中点在 $y=\ln x$ 的切线的斜率。(此处的中点意为函数图像上的中点)

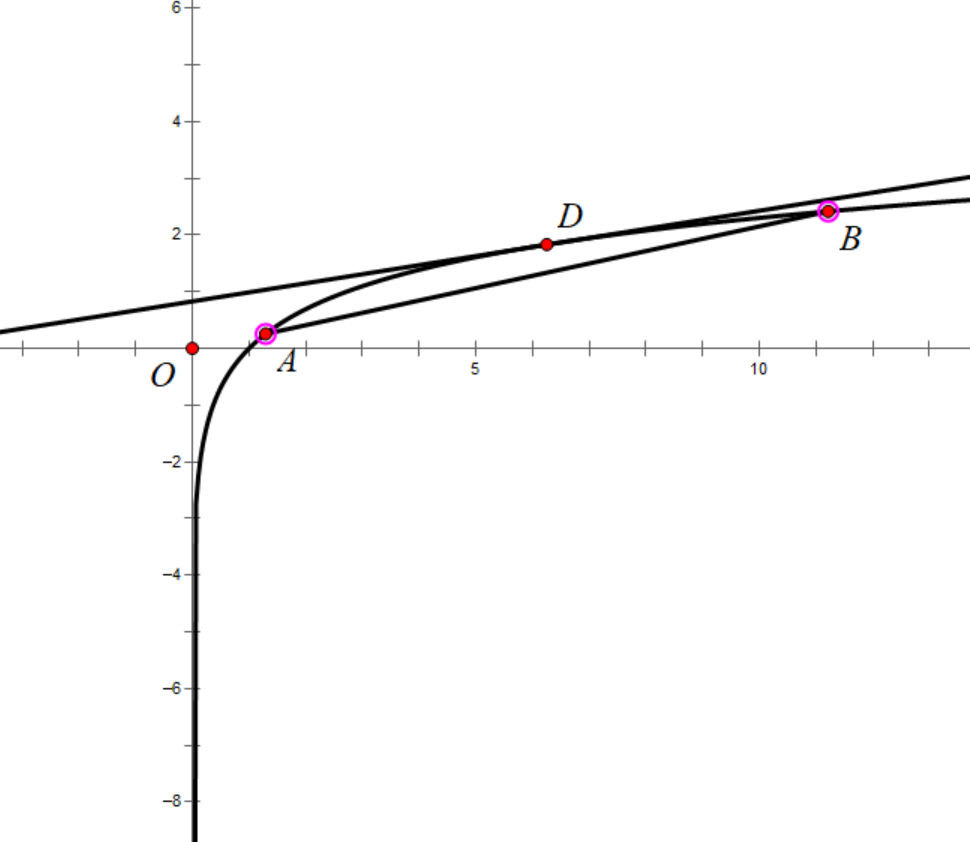
注：这也是为什么特地将不等号写为 \("\leq"\) 的原因之一，当 \(B\) 无限接近 \(A\) ，斜率变成了切线的斜率^[1]，与 \(l\) 的斜率相等。

实际上，在 \(k_1\) 与 \(k_2\) 作比较时应当想到拉格朗日中值定理，此定理表述为：

\[对于f(x)，如果满足：\\ (1)f(x)在区间(a,b)上可导；\\ (2)f(x)在区间[a,b]上连续.\\ 则：必定\exist \xi \in (a,b)，使得f^{'}(\xi)=\frac{f(a)-f(b)}{a-b}. \]

该定理的几何直观性非常强，即 \(\exist \xi\) 一点 \(\in(a,b)\) ，且改点的斜率与 \(k_{AB}\) 相同(或者说是与 \(AB\) 平行)，但是该定理不需要深入证明，并且高中数学答卷中不可使用，但对于某些问题的本质研究有一定辅助的作用。

其实有不少题目都是以此作为背景，此类题目一般表述为： \(是否\exist x_1 ,x_2\ 使得\frac{f(x_1)-f({x_2})}{x_1-x_2}=f^{'}(\frac{x_1+x_2}{2})成立\) 或者更特殊的 \(x_1<x_2且两者均为f(x)的零点，判断f^{'}(\frac{x_1+x_2}{2})(or\ f^{'}(\sqrt{x_1x_2}))的正负性\) ^[2]而对于函数 \(y=\ln x\) 则表明 \(\xi<\frac{x_1+x_2}{2}\) 。此类题目其实和本结论关系较小(但其实大部分最后的证明也是基于本结论)，一般利用类似前面的证明方法证明即可，在此仅作说明。

3. Application in High School Math(在高中数学中的应用)

①韦达定理

如果仔细观察的话会发现，许多导数题涉及双变量及一元二次方程(导数零点常是)，而本结论的形式 \((x_1+x_2)\) 与 \(\sqrt{x_1x_2}\) 就不得不想到韦达定理。在此类题目中，往往一次项系数或者常数项为常数，进而便于不等式放缩。

以 2018 年全国卷 I 为例：

\[已知函数f(x)=\frac 1{x}-x+a\ln x\ (a>2)\quad\exist两个极值点x_1和x_2且0<x_1<x_2，求证：\\ \frac{f(x_1)-f(x_2)}{x_1-x_2}<a-2. \]

证明：

\[f^{'}(x)=-\frac 1{x^2}-1+\frac{a}{x}=-\frac{1}{x^2}(x^2-ax+1),\quad \therefore x_1x_2=1\\ LHS=\frac{\frac{1}{x_1}-x_1+a\ln {x_1}-\frac 1{x_2}-x_2+a\ln {x_2}}{x_1-x_2}\\ =\frac{-2(x_1-x_2)+a(\ln{x_1}-\ln{x_2})}{x_1-x_2}\\ =-2+a\frac{\ln{x_1}-\ln{x_2}}{x_1-x_2}\quad\quad\quad\quad\ \ \ \\ <-2+a\frac{1}{\sqrt{x_1x_2}}=a-2.\quad\quad证毕 \]

②某一类极值点偏移

极值点偏移是一类“入门题”，较难的极值点偏移一般通过复杂的参数设置，分段设置函数实现，但大同小异。对于 \(f(x)\) 中有参数，但是证明的式子中却没有参数的题目，一般暗示参数并没有什么真正价值，理应消去。简单形式的双变量用合分比性质即可简单解决，在此仅为强调该不等式的强大及辅助理解此不等式。

例：

\[对于函数f(x)=e^x-mx有两个零点\quad x_1,x_2\ 且<0x_1<x_2.求证：\\ x_1\cdot x_2<1. \]

证明：

\[m=\frac{e^x}{x}\quad(消参)\\ \frac{e^{x_1}}{x_1}=\frac{e^{x_2}}{x_2}\Rightarrow x_1-\ln {x_1}=x_2-\ln{x_2}\\ \Rightarrow\frac{x_1-x_2}{\ln{x_1}-\ln{x_2}}=1.\\ \therefore x_1\cdot x_2={\sqrt{x_1x_2}}^2<{(\frac{x_1-x_2}{\ln{x_1}-\ln{x_2}})}^2=1.\quad证毕 \]

注：常常由简单函数添加不容易“分离”的参数使题目难度增加，例如这个函数 \(y=e^x-x\) 实际上还可以这样处理：

\[令\ e^x-x=a\Rightarrow x=\ln{(x+a)}\\ 构造函数f(x)=x-\ln{(x+a)} \]

这样处理后的函数相对较为高级。

③多项式化处理(较为灵活)

众所周知涉及双变量不等式的题目要消元，构造单变量函数求导(不停地求导)即可做出。但实际上这样比较繁琐，这个不等式还有另一个很强的作用就是把超越式 \(\ln x\) 消去，转化为多项式(多项式可以因式分解)。

注：这样处理还有一个很重要的原因在于此不等式较强(一般放缩不会过度)，且等号成立条件一般和题目相同(如不同，则慎用)。

例：

• (泉州市一模)
  \[已知函数f(x)=\frac 1 {2}x^2+bx+a\ln x\quad(a+b=-1\ 且a>1(即1为极大值点))\\ 若\exist x_0使得f(x_0)=f(1)\quad(x_0\neq1),求证：a<x_0<a^2. \]
  证明：
  \[f^{'}(x)=x-(a+1)+\frac a x\\ =\frac{1}{x}(x^2-(a+1)x+a)\\ =\frac 1 x (x-a)(x-1)\quad\quad\\ \therefore f(x)在(0,1),(a,+\infty)单调递增，在(1,a)单调递减\Rightarrow x_0>a\\ 再来说明右边：x_0<a^2\Leftrightarrow f(x_0)<f(a^2)\\ 化单变量为双变量寻求对称：x_2=a^2,x_1=1\\ 求差：f(x_2)-f(x_0)=f(x_2)-f(x_1)\\ =\frac 1 2 (x_2^2-x_1^2)+b(x_2-x_1)+a(\ln{x_2}-\ln{x_1})\\ =(x_2-x_1)[\frac{x_1+x_2}{2}+b+a\frac{\ln{x_2}-\ln{x_1}}{x_2-x_1}]\\ \]
  上式=(x_2-x_1)(m-(a+1)+\frac a m)\=\frac{x_2-x_1}{m}(m-a)(m-1)>0.\quad证毕
  \[ \]
  已知函数f(x)=e^{2x}+(a-ax)ex,x_1和x_2为f(x)的两个极值点且0<x_1<x_2\若：x_1x_2+m(x_1+x_2)<0恒成立，求m的取值范围.
  \[ 证明： \]
  注意到：f(x)=e^x(2ex-ax)\Rightarrow\frac{e^{{x_1}}{x_1}=\frac{e}{x_2}}{x_2}\
  \Rightarrow\frac{x_1-x_2}{\ln{x_1}-\ln{x_2}}=1.\
  原不等式\Leftrightarrow-m>\frac{x_1x_2}{x_1+x_2}\quad(不齐次)\
  \because x_1+x_2\geq2\sqrt{x_1x_2}\quad(其实用x_1x_2\leq\frac{(x_1+x_2)^2}{4}也可以，读者可自行尝试)\
  \frac{x_1x_2}{x_1+x_2}\leq\frac{\sqrt{x_1x_2}}{2}<\frac 1 2 \frac{x_1-x_2}{\ln{x_1}-\ln{x_2}}=\frac 1 2.\
  \therefore m\leq -\frac 1 2.
  \[ \]

---

1. 其实这也是切线的定义，再者，事实上： \(\lim_{x_2\to x_1}\frac{x_1-x_2}{\ln {x_1}-\ln{x_2}}=\frac{1}{(\ln{x_1})^{'}}=x_1=\lim_{x_2\to x_1}\frac{x_1+x_2}{2}\) ↩︎

2. 实际上这就是以罗尔中值定理为背景，有兴趣可以了解。 ↩︎