二分图最大分配

二分图是一个无向图，分为x，y两部分，x部中的点与y中的点往往会存在多条无向边，若x1与y2之间存在一条边，那么x1与y2可以“分配”，当然每个点部止局限于只有一条边，可以有多条，所以又有多种分配方法，为达到让这个二分图中分配数量最大，即使x1与y2可以“分配”也只是暂时的，因为要为其他点“让步”，举个例子：

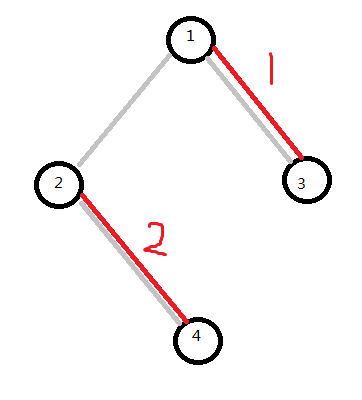图中，点1到点2有一条边，点1到点3有一条边，点2到点4有一条边

就“择近原则”，点1可以首先和点2“分配”，但点3发现自己只有点1可以“分配”，于是就向点1提出要求“分配”，可是点1已经被“分配过了”，于是点1就去找点2商量问它可不可以找另一个点“分配”，点2就去询问点4能否“分配”，发现点4还没有被“分配”，也就是说点2可以找另一个点分配，于是返回true，不和点1“分配”了，和点4分配，点1得到true便与点3“分配”了

细心的人可能会发现，如果像开始那样：点1与点2分配，那么只有1个“分配组”，而经过这一系列算法（匈牙利算法）而拓展路线（增广路）便有2个“分配组”，这就称为二分图最大分配

题目链接

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
int m;
int n;
int x,y;
int ans;
int match[210];                                  //记录分配目标 
int put[110][3];                                 //输出 
bool book[210];                                  //记录剪枝 
bool way[210][210];                              //记录无向图的边 
inline int read()                                //快速读入 
{
    int sign=1,num=0;
    char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')sign=-1;ch=getchar();}
    while(isdigit(ch)){num=num*10+(ch-'0');ch=getchar();}
    return sign*num;
}
void init()                                      //读入函数 
{
    m=read();
    n=read();
    while(x!=-1&&y!=-1)
    {
        x=read();                                //无向边存两次 
        y=read();
        way[x][y]=true;
        way[y][x]=true;
    }
}
bool dfs(int x)
{
    for(int y=m+n;y>0;--y)
    {
        if(way[x][y]&&book[y]==false)            //枚举点x的边 
        {
            book[y]=true;                        //记录点y已被查找（并非分配） 
            if(match[y]==0||dfs(match[y]))       //若y没有被分配或与y分配的人还有"退"的余地 
            {
                match[x]=y;                      //储存分配目标 
                match[y]=x;
                return true;
            }
        }
    }
    return false;
}
int main()                                       //看代码建议从mian函数看起 
{
    init();
    for(int i=1;i<=m+n;++i)                      //枚举点 
    {
        memset(book,false,sizeof(book));
        dfs(i);
    }
    for(int i=1;i<=m+n;++i)
        if(match[i]!=0&&match[match[i]]!=0)       //防止重复输出 
        {
            put[++ans][1]=i;
            put[ans][2]=match[i];
            match[match[i]]=0;
        }
    if(ans==0)                                   //特判 
    {
        puts("No Solution!");
        return 0;
    }
    printf("%d",ans); 
    for(int i=1;i<=ans;++i)
        printf("\n%d %d",put[i][1],put[i][2]);
}